哈希函数与哈希一致性

Hash

哈希函数是想把不同的输入通过某种映射关系输出不同的值，尽可能地不要冲突。

1. 哈希函数的输入域可以近似看成无穷大
2. 相同的输入一定输出相同的值
3. 不同的输入可能会产生相同的输出，这种情况称为碰撞 ，这种概率极低
4. 哈希函数最重要的性质：不同的输入几乎可以均匀地散列在输出域中

**经过哈希算法后得到一个很大的输出值，这些值可以保证等概率的均匀散列，但是这些输出值的范围是很大的，如果再对该数值取模 %m 就可以将所有的输出值进一步集中到 [0, m-1] 这个范围内，并且映射到 [0, m-1] 每个值上的数量也可以保证几乎是等概率的。取模操作就是进一步帮我们将所有输出值又散列在了一个更集中的范围里 **

HashTable

哈希表的主表可以看成一个数组，数组的长度就代表了散列区间的长度，就是m的取值影响的。每一个数组元素都是一个单链表的头，经过取模之后如果散列到相同数组元素索引，就自动形成单链表。

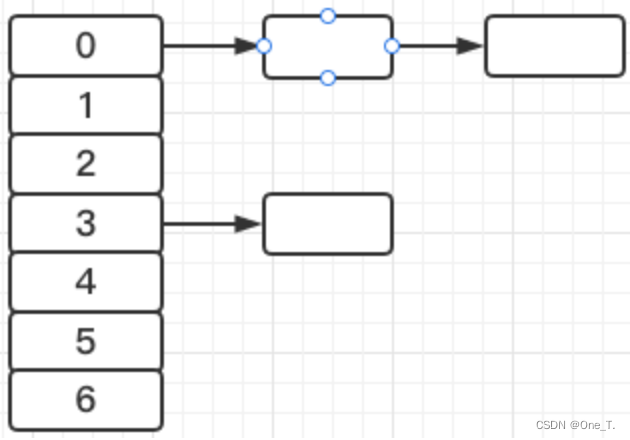
扩容

当单链表的长度达到某个限度后，哈希表会扩容。扩容的逻辑就是：原先我是把所有元素散列在了7个位置，那现在我决定将所有元素散列到14个位置上，所以数组长度会变为14，并且所有元素最终取模后的结果也要重新计算。

在java中，还对单链表实现了优化，比如说用树代替单链表

例题

设计一种结构，在该结构中有如下三个功能:

1. insert (key)：将某个key加入到该结构，做到不重复加入
2. delete(key)：将原本在结构中的某个key移除
3. getRandom()：等概率随机返回结构中的任何一个key。

要求：Insert、delete和getRandom方法的时间复杂度都是O(1)

public Hash(){
   IntKeyMap = new HashMap<>();
   KeyIntMap = new HashMap<>();
   size = 0;
}

public void insert(K key){
   if (!KeyIntMap.containsKey(key)){
      KeyIntMap.put(key, size);
      IntKeyMap.put(size++, key);
   }
}

// 删除后index就不连续了，那么随机的时候有很多数都不是连着的了。所以每次用最后一个填补要删除的那个
public void delete(K key){
   if (KeyIntMap.containsKey(key)){
      // 获得要删除的key的index
      int index = KeyIntMap.get(key);
      // 获得当前表中最后一个index
      int lastIndex = --size;
      // 获得当前表中最后一个index对应的key
      K tail = IntKeyMap.get(lastIndex);

      // 填补
      KeyIntMap.put(tail, index);
      IntKeyMap.put(index, tail);

      // 删除最后的
      IntKeyMap.remove(lastIndex);
      KeyIntMap.remove(key);
   }
}

public K getRandom(){
   if (size == 0)
      return null;
   int randomIndex = (int) (Math.random() * size);
   return IntKeyMap.get(randomIndex);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

hash一致性问题

在数据服务器上，通常有多台服务器存储数据，并且每台存储的都不一样，那么一条数据如何来决定存储在哪台数据服务器上呢？ 通常来说是根据哈希算法求哈希值然后取模来决定存储在哪台数据服务器上。这样能保证每台服务器上的数据均衡，并且种类也均衡。但是通过使用哪个字段来算哈希就很讲究了。继续之前，先得明白什么是 负载均衡

负载均衡是指在一台服务器上，包含高频数据、中频数据、低频数据，并且数量相当，就可以认为该服务器负载均衡。(这里的高中低频是指被搜索的频率)

如果以字段国家名来哈希散列，并且有三台服务器，那必然有一台负载不均衡。因为高频数据只有中美两个国家。

经典方法的局限

当突然新增数据服务器时，所有存储的数据都得全部重新计算哈希值，减少服务器时也是一样。用什么方法才能让这样服务器的变动导致的开销变小呢？

哈希一致性

1. 首先把哈希函数的输出域想象成一个环形域。

2. 假设此时有三台数据服务器，算完哈希值为5亿，6207亿，2万亿，根据哈希值后散列成如下位置：

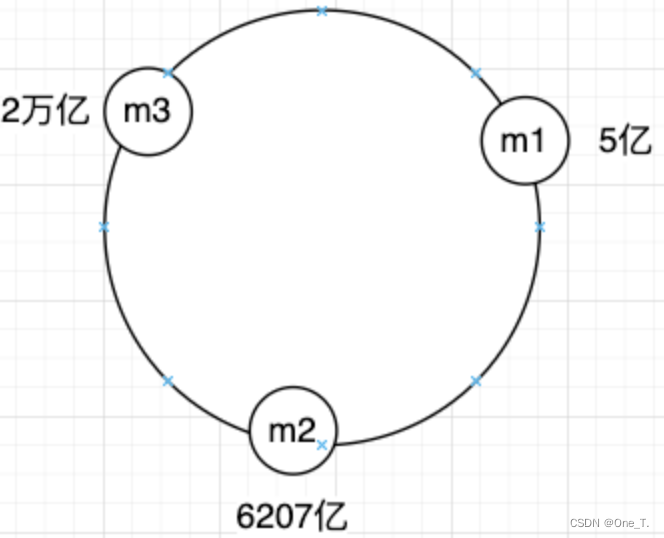    	![](https://img-blog.csdnimg.cn/d3c22d10d6574c57bc4e1a7fb183eb5b.png)
   1

3. 假如有条数据算完哈希后要插入的位置如图所示，那应该存储到哪个服务器上呢？顺时针最近的服务器

​ 这三台服务器的哈希结果会按照顺序存储在数组中，如何确定数据在哪台服务器上呢？将该数据的哈希结果在数组中用二分查找找到该去哪台服务器。

当新增一台服务器时，只需要一小部分的数据迁移就可以实现服务器的扩容，代价比之前小了很多。

m2和m4之间的区域本来是归m3管的，现在新加了m4后，只需要要将这部分数据迁移至m4上即可，其余所有的都不用动。减少服务器时也一样。

这种结构仍然存在两个问题

1. 服务器很少时，如何能均分这个环形的输出域？ 上图三台服务器可不一定是均分输出域的
2. 即便均分了输出域，当新加或者减少服务器时，立刻又不均衡了。加入上述三台服务器均分输出域，每台负责$1/3$ ，并且m4是m2和m3的中点，此时m1，m2负责$1/3$ ，而m3，m4只负责$1/6$

这两个问题都可以用虚拟结点技术解决

虚拟结点

分别给三台服务器分配1000个字符串，每个字符串都可以代表其所属的服务器，如下：

$m1(a_1,a_2,...,a_{1000})$

$m2(b_1,b_2,...,b_{1000})$

$m3(c_1,c_2,...,c_{1000})$

每台机器上的1000个字符串分别算一个哈希值然后去环上占位，这样环上一共就有3000个节点，这样就可以保证每台机器管辖的输出域大致相等。如果有新的服务器要加入，同样用1000个结点上去占位，这样新的机器从其他三台那里抢过来的数量几乎相等。

此外，虚拟结点还能根据服务器性能的差异动态管理服务器。假如m1性能特别强悍，那我就可以给它分配2000个字符串去占位，某台机器的性能比较弱就可以分配较少的字符串。