• 2022牛客蔚来杯补题（第九场）

    A （签到）Car Show

    题意：在长度为n的数组（a[i]<=m)内，包括多少个区间[l,r]满足区间中包含1-m所有数

    题解：双指针

    code：

    1. #include
    2. using namespace std;
    3. typedef long long ll;
    4. const int N = 1e5 + 20;
    5. int n, m, a[N], cnt[N], sum;
    6. ll ans;
    7.  
    8. int main(){
    9.     scanf("%d%d", &n, &m);
    10.     for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    11.     for(int l = 1, r= 1; l <= n; l++){
    12.         while(r <= n && sum < m){
    13.             int res = a[r];
    14.             if(!cnt[res]) sum++;
    15.             cnt[res] ++;
    16.             r++;
    17.         }
    18.         if(sum == m)
    19.             ans += n - r + 2;
    20.         cnt[a[l]]--;
    21.         if(!cnt[a[l]]) sum--;
    22.     }
    23.     printf("%lld\n", ans);
    24.     return 0;
    25. }

    B（DP）Two Frogs

    题意：有n块荷叶排成一排，从第i个荷叶起跳可以跳到[i + 1, i + a[i]]块荷叶（随机等概率），存在两只青蛙初始都在第一块荷叶，求两只青蛙以相同步数到达第n块荷叶的概率。

    题解：

            f[i][j]：跳跃i步到达j的概率

            方程：f[i][j + res] += f[i - 1][j] * \frac{1}{res}

            PS:如果正着推时间复杂度为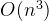O({n}^{3})，考虑处于当前状态对后面状态的影响（区间），可以用前缀和处理

    code：

    1. #include
    2. using namespace std;
    3. typedef long long ll;
    4. const int N = 8010;
    5. const int mod = 998244353;
    6. int n, a[N];
    7. ll f[N][N], b[N];
    8.  
    9. ll ksm(ll a, ll b){
    10.     ll res = 1;
    11.     while(b){
    12.         if(b & 1) res = res * a % mod;
    13.         a = a * a % mod;
    14.         b >>= 1;
    15.     }
    16.     return res;
    17. }
    18.  
    19. int main(){
    20.     scanf("%d", &n);
    21.     for(int i = 1; i <= n; i++){
    22.         scanf("%d", &a[i]);
    23.         b[i] = ksm(a[i], mod - 2);
    24.     }
    25.     f[0][1] = 1;
    26.     for(int i = 1; i < n; i++){ //跳跃i步
    27.         for(int j = 1; j <= n; j++){ // 到达位置j
    28.             int res = a[j];
    29.             f[i][j + 1] = (f[i][j + 1] + f[i - 1][j] * b[j] + mod) % mod;
    30.             f[i][j + res + 1] = (f[i][j + res + 1] - f[i - 1][j] * b[j] + mod) % mod;
    31.         }
    32.         for(int j = 1; j <= n; j++){
    33.             f[i][j] = (f[i][j] + f[i][j - 1] + mod) % mod;
    34.         }
    35.     }
    36.     ll ans = 0;
    37.     for(int i = 1; i < n; i++){
    38.         ans = (ans + f[i][n] * f[i][n] % mod + mod) % mod;
    39.     }
    40.     printf("%lld\n", ans);
    41.     return 0;
    42. }

    C（树上差分 / 树链刨分）Global Positioning System

    D

    E（构造）Longest Increasing Subsequence

    题意：构造一个长度小于100的序列，使得序列中最长上升子序列恰好有m个

    题解：考虑两个数两个数为一组（例如： 2 1  4 3  6 5...），假设有x组，就会形成2^{x}个最长上升子序列，然后考虑在组与组之间插入数【将m拆成二进制】

    PS：插入的数也要发挥他的作用

    code:

    1. #include
    2. using namespace std;
    3. const int N = 110;
    4. int t, m;
    5. struct NODE{
    6.     int id, x;
    7. }node[N];
    8.  
    9. bool cmp(NODE a, NODE b){
    10.     return a.x < b.x;
    11. }
    12.  
    13. int main(){
    14.     scanf("%d", &t);
    15.     while(t--){
    16.         scanf("%d", &m);
    17.         if(m == 1){
    18.             printf("1\n1\n");
    19.             continue;
    20.         }
    21.         vector<int> ans;
    22.         bitset<32> bit(m);
    23.         int k = 31, res = 100;
    24.         while(!bit[k]) k--;
    25.         ans.push_back(2 * k - 1);
    26.         ans.push_back(2 * k);
    27.         int ned = 0, cnt = 0;
    28.         while(--k >= 0){
    29.             ned++;
    30.             if(bit[k]){
    31.                 for(; cnt < ned; cnt++) ans.push_back(res), res--;
    32.             }
    33.             if(k){
    34.                 ans.push_back(2 * k - 1);
    35.                 ans.push_back(2 * k);
    36.             }
    37.         }
    38.         reverse(ans.begin(), ans.end());
    39.         int n = ans.size();
    40.         printf("%d\n", n);
    41.         for(int i = 0; i < n; i++){
    42.             node[i].id = i;
    43.             node[i].x = ans[i];
    44.         }
    45.         sort(node, node + n, cmp);
    46.         for(int i = 0; i < n; i++){
    47.             ans[node[i].id] = i + 1;
    48.         }
    49.         for(int i = 0; i < n; i++){
    50.             printf("%d ", ans[i]);
    51.         }
    52.         puts("");
    53.     }
    54.     return 0;
    55. }

    F

    （队友补了等于我补了）

    G（SAM / Manache / PAM）Magic Spells

    题意：求k个串中的不同的公共回文串

    题解：解法有很多

    code：【队友打的】

    1. #include 
    2. #define ll long long
    3. using namespace std;
    4.  
    5. const int N = 3e5 + 50;
    6.  
    7. struct node {
    8.     int len, link, ch[26], id;
    9. }st[N << 1];
    10. int sz, last;
    11.  
    12. void sam_init () { sz = last = 1; }
    13.  
    14. void sam_extend (int c, int id) {
    15.     int cur = ++ sz, p = last;
    16.     st[cur].len = st[p].len + 1, last = cur;
    17.     st[cur].id = id;
    18.     for ( ; p && ! st[p].ch[c]; p = st[p].link) st[p].ch[c] = cur;
    19.     if (! p) st[cur].link = 1;
    20.     else {
    21.         int q = st[p].ch[c];
    22.         if (st[p].len + 1 == st[q].len) st[cur].link = q;
    23.         else {
    24.             int clone = ++ sz;
    25.             st[clone].len = st[p].len + 1;
    26.             st[clone].link = st[q].link;
    27.             st[clone].id = st[q].id;
    28.             memcpy (st[clone].ch, st[q].ch, sizeof (st[q].ch));
    29.             for ( ; p && st[p].ch[c] == q; p = st[p].link) st[p].ch[c] = clone;
    30.             st[q].link = st[cur].link = clone;
    31.         }
    32.     }
    33. }
    34.  
    35. char s[5][N], str[N << 1];
    36. int a[N << 1], b[N], n, k;
    37. int g[N << 1], f[N << 1];
    38. int p[N << 2], lef[N << 1];
    39.  
    40. void manacher (char* s, int len) {
    41.     for (int i = 1, r = 0, mid = 0; i < len; i ++) {
    42.         if (i <= r) p[i] = min (p[(mid << 1) - i], r - i + 1);
    43.         while (s[i - p[i]] == s[i + p[i]]) ++ p[i];
    44.         if (p[i] + i > r) r = p[i] + i - 1, mid = i;
    45.     }
    46. }
    47.  
    48. bool vis[N << 1];
    49.  
    50. void solve () {
    51.     str[0] = '~', str[1] = '|';
    52.     int len = 1;
    53.     for (int i = 0; i < n; i ++) 
    54.         str[++ len] = s[0][i], str[++ len] = '|';
    55.     manacher (str, len);
    56. //     printf("%s\n", str);
    57.     for (int i = 1; i <= n; i ++) lef[i] = i;
    58.     for (int i = 2; i < len; i ++) {
    59. //         printf("i = %d, p = %d\n", i / 2, p[i] - 1);
    60.         lef[(i + p[i]) / 2 - 1] = min (lef[(i + p[i]) / 2 - 1], (i - p[i]) / 2 + 1);
    61.     }
    62.     for (int i = n; i >= 2; i --) lef[i - 1] = min (lef[i - 1], lef[i] + 1);
    63. //     for (int i = 1; i <= n; i ++) 
    64. //         printf("lef = %d\n", lef[i]);
    65.     ll ans = 0;
    66.     for (int i = 1; i <= sz; i ++) {
    67.         int x = st[i].id - g[i] + 1, y = st[i].id;
    68.         if (x <= y) {
    69.             if (vis[st[i].id]) continue;
    70.             int nx = lef[st[i].id], ny = st[i].id;
    71.             if (x <= nx && (ny - nx + 1 > st[st[i].link].len)) {
    72.                 ans ++;
    73.                 vis[st[i].id] = true;
    74.             }
    75. //             printf("len = %d\n", st[st[i].link].len);
    76. //             printf("i = %d, x = %d, y = %d, nx = %d, ny = %d\n", st[i].id, x, y, nx, ny);
    77.         }
    78.         
    79.     }
    80.     printf("%lld\n", ans);
    81. }
    82.  
    83. int main () {
    84. //     freopen("in.txt", "r", stdin);
    85. //     freopen("test.txt", "w", stdout);
    86.     scanf ("%d%s", &k, s[0]);
    87.     sam_init ();
    88.     n = strlen (s[0]);
    89.     for (int i = 0; i < n; i ++) sam_extend (s[0][i] - 'a', i + 1);
    90.     for (int i = 1; i <= sz; i ++) b[st[i].len] ++;
    91.     for (int i = 1; i <= n; i ++) b[i] += b[i - 1];
    92.     for (int i = sz; i >= 1; i --) a[b[st[i].len] --] = i;
    93.     for (int i = 1; i <= sz; i ++) g[i] = st[i].len;
    94.     
    95.     for (int j = 1; j < k; j ++) {
    96.         scanf ("%s", s[j]);
    97.         for (int i = 1; i <= sz; i ++) f[i] = 0;
    98.         for (int i = 0, v = 1, len = 0; s[j][i]; i ++) {
    99.             int c = s[j][i] - 'a';
    100.             while (v && ! st[v].ch[c]) v = st[v].link, len = st[v].len; 
    101.             if (! v) v = 1, len = 0;
    102.             if (st[v].ch[c]) ++ len, v = st[v].ch[c]; // 匹配成功，那么匹配出去即可。
    103.             f[v] = max (f[v], len);  // 更新该结点的长度
    104.         }
    105.         for (int i = sz; i >= 1; i --) 
    106.             f[st[a[i]].link] = max (f[st[a[i]].link], f[a[i]]);  
    107.         for (int i = 1; i <= sz; i ++) g[i] = min (f[i], g[i]);
    108.     }
    109. //     printf("%d\n", *max_element(g + 1, g + sz + 1));
    110. //     for (int i = 1; i <= sz; i ++) {
    111. //         printf("i = %d, len = %d\n", st[i].id, g[i]);
    112. //     }
    113.     solve ();
    114.     return 0;
    115. }

    H

    I（dp 单调栈优化）The Great Wall II

    题意：一个长的为n的数组分成k段，求每一段的最大值之和最小

    题解：dp[i][j] : 前i个数分成j段的最小值

            dp[i][j] = min\left \{ dp[k][j - 1] + max(a[k + 1] ~ a[i]) \right \}

    code:

    1. #include
    2. using namespace std;
    3. const int N = 8010;
    4. const int INF = 0x3f3f3f3f;
    5. int n, a[N], dp[N][2];
    6. struct NODE{
    7.     int x, f, minn;
    8. };
    9.  
    10. int main(){                    
    11.     scanf("%d", &n);
    12.     for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    13.     for(int i = 1; i <= n; i++){
    14.         dp[i][1] = max(dp[i - 1][1], a[i]);
    15.     }
    16.     printf("%d\n", dp[n][1]);
    17.     for(int j = 2; j <= n; j ++){
    18.         stack st;
    19.         for(int i = 1; i <= n; i++){
    20.             dp[i][j & 1] = 0;
    21.         }
    22.         for(int i = 1; i <= n; i++){
    23.             if(i < j){
    24.                 dp[i][j & 1] = dp[i][(j - 1) & 1];
    25.                 continue;
    26.             }
    27.             if(st.size() && a[i] >= st.top().x){ // 弹出
    28.                 int dpmin = dp[i - 1][(j - 1) & 1];
    29.                 while(st.size() && a[i] >= st.top().x){
    30.                     NODE res = st.top();
    31.                     st.pop();
    32.                     dpmin = min(dpmin, res.f);
    33.                 }
    34.                 dp[i][j & 1] = a[i] + dpmin;
    35.                 if(st.size()){
    36.                     dp[i][j & 1] = min(st.top().minn, dp[i][j & 1]);
    37.                 }
    38.                 st.push({a[i], dpmin, dp[i][j & 1]});
    39.             }
    40.             else{
    41.                 dp[i][j & 1] = a[i] + dp[i - 1][(j - 1) & 1];
    42.                 if(st.size()){
    43.                     dp[i][j & 1] = min(st.top().minn, dp[i][j & 1]);
    44.                 }
    45.                 st.push({a[i], dp[i - 1][(j - 1) & 1], dp[i][j & 1]});
    46.             }
    47.         }
    48.         printf("%d\n", dp[n][j & 1]);
    49.     }
    50.     return 0;
    51. }

    J

    K

  • 相关阅读:
    【DPDK】使用 Open vSwitch * 采用 DPDK 帧间 VM NFV 应用程序
    git命令合并某一个分支的某个commit到目标分支
    Spring学习之ImportBeanDefinitionRegistrar接口
    C++ 嵌套 switch 语句
    钟汉良日记：出门在外靠什么？
    对Redis布隆过滤器的实现
    【无标题】
    微服务_fegin
    2023年天津财经大学珠江学院专升本管理学原理专业考试大纲
    论文阅读: Disentangled lmage Colorization via Global Anchors
  • 原文地址：https://blog.csdn.net/Galaxy_Su/article/details/126725548