Codeforces Round #815 (Div. 2)

A. Burenka Plays with Fractions

题目链接：Problem - A - Codeforces

 样例输入：

8
2 1 1 1
6 3 2 1
1 2 2 3
0 1 0 100
0 1 228 179
100 3 25 6
999999999 300000000 666666666 100000000
33 15 0 84

样例输出：

1
0
2
0
1
1
1
1

题意：给你两个分数a/b,c/d,你每次操作可以将任意一个分数的分母或者分子乘以一个数，但是不能使得分母为0，问最少需要几次操作可以使得两个分数的值相等

分析：首先，很容易想到的一点就是答案不会超过2，因为对于任意的两个分数，我们分别给两个分数的分子乘以0那么就会使得两个数相同，那么下面我们只需要讨论一下需要0次或者1次的情况即可：

需要0次的情况很好分析，就是一开始两个数就相同，我们可以直接用浮点数进行运算后比较，不需要考虑精度，因为两个分数如果相同的话是不会有精度损失的

需要一次的情况就是说我用第一个分数除以第二个分数或者用第二个分数除以第一个分数得到的结果中至少有一个为0，但是需要注意的一个特殊情况就是其中一个分数本身就是0，我们可以特判一下

下面是代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
using namespace std;
const int N=1e5+10;
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		long long a,b,c,d;
		scanf("%lld%lld%lld%lld",&a,&b,&c,&d);
		if(1.0*a/b==1.0*c/d) puts("0");
		else if(a==0||c==0) puts("1");
		else if(a*d%(b*c)==0||b*c%(a*d)==0) puts("1");
		else puts("2");
	}
	return 0;
} 

B. Interesting Sum

题目链接：Problem - B - Codeforces

 样例输入：

4
8
1 2 2 3 1 5 6 1
5
1 2 3 100 200
4
3 3 3 3
6
7 8 3 1 1 8

样例输出：

9
297
0
14

题意：给你一个长度为n的数组，让选择一个l，r(1<=l<=r<=n)求max(a1,a2,…,al−1,ar+1,ar+2,…,an)−min(a1,a2,…,al−1,ar+1,ar+2,…,an)+max(al,…,ar)−min(al,…,ar)

分析：其实容易发现的一点就是max(a1,a2,…,al−1,ar+1,ar+2,…,an)和max(al,…,ar)中其中有一个必然是数组中的最大值，因为他们是不相交但是并集为全集的两块区域，同理min(a1,a2,…,al−1,ar+1,ar+2,…,an)和min(al,…,ar)中也必然有一个数组中的最小值。那么我们就来想能不能让另一个数分别取得次大值和次小值呢？其实是可以的，我不妨假设数组中最大值最小值次大值次小值的位置分别为i,j,k,l,那么必然有最大值和次大值中的一个与最小值和次小值中的一个相邻，那么直接令这两个坐标的较小值作为l，较大值作为r即可。所以无论如何都存在一种方案使得两个max分别取最大值和次大值，两个min分别取最小值和次小值

下面是代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
using namespace std;
const int N=1e5+10;
int a[N];
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n;
		scanf("%d",&n);
		for(int i=1;i<=n;i++) scanf("%d",&a[i]);
		long long ans=0;
		sort(a+1,a+n+1);
		ans=a[n]+a[n-1]-a[1]-a[2];
		printf("%lld\n",ans);
	}
	return 0;
}

C. Corners

题目链接：Problem - C - Codeforces

 样例输出：

4
4 3
101
111
011
110
3 4
1110
0111
0111
2 2
00
00
2 2
11
11

样例输出：

8
9
0
2

题意：给出一个n*m的矩形，每个格子里面有一个1或者0，我们每次可以把一个‘L’型的区域全部变成0，进行该操作的前提是这个‘L’型的区域里面至少含有一个1，‘L’是一个固定大小为3的区域。求出最多可以操作的次数。

分析：除了第一次之外，我们可以保证每次操作只消去一个1，因为我们第一次操作后至少存在两个相邻单元格均为0，那么很显然我们可以用L的一遍覆盖两个相邻的0，用另一端去覆盖一个1，这样我们每次操作都只会消去一个1，这样肯定是最优的，所以问题就是我们第一次操作会消去几个1，如果第一次操作只消去一个1，那么操作次数就是1的个数，如果第一次操作至少消去2个1，那么答案就是1的个数-1，如果第一次操作至少消去3个1，那么答案就是1的个数-2，第一次操作至少消去1的个数取决于长度为2的小正方形中含有0的最多数目，如果含有2个0及以上，那么就可以消掉一个1，如果含有1个0，就至少需要消掉两个1，如果n*m的矩形全为1，那么第一次操作至少消掉3个1，这个画图就很好理解了

细节见代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
using namespace std;
const int N=1e3+10;
char s[N][N];
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n,m;
		scanf("%d%d",&n,&m);
		int mn=4,ans=0;
		for(int i=1;i<=n;i++)
		{
			scanf("%s",s[i]+1);
			for(int j=1;j<=m;j++)
				if(s[i][j]=='1') ans++; 
		}
		for(int i=1;i<n;i++)
		for(int j=1;j<m;j++)
		{
			int cnt=0;
			if(s[i][j]=='1') cnt++; 
			if(s[i+1][j]=='1') cnt++;
			if(s[i][j+1]=='1') cnt++;
			if(s[i+1][j+1]=='1') cnt++;
			mn=min(mn,cnt);
		}
		if(mn>=3) ans-=(mn-2);
		printf("%d\n",ans); 
	}
	return 0;
}

D1. Xor-Subsequence (easy version)

题目链接：Problem - D1 - Codeforces

样例输入： 

3
2
1 2
5
5 2 4 3 1
10
3 8 8 2 9 1 6 2 8 3

样例输出：

2
3
6

这道题原题题意描述的不是很清楚，我再下面重新描述一下：

题意：给定一个长度为n的数组，每个数组的元素都是小于等于200的，现在要我们求一个最长的序列b1,b2,……bm(0<=b1a_b_i" role="pre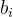sentation" style="position: relative;">a_b_i$\text{a\_b\_i}$^b_(_i+_1_)" role="presentation" style="position: relative;">b_(_i+_1_)$\text{b\_(\_i+\_1\_)}$<a_b_(i+1_)" role="presentation" style="position: relative;">a_b_(i+1_)$\text{a\_b\_(i+1\_)}$^成立，问m的最大值是多少？

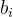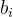分析：这道题给我的第一感觉就是一种可以用类似于最长上升子序列的解决方法解决，也就是设f[i]表示从0~i的数组中满足条件的最长序列长度，然后就是O(n^2)动态规划枚举求解，但是n的范围3e5，这样是肯定会超时的，于是我们可以思考一下能不能从不等式中进行一部分枚举优化，我们发现，a的值是小于等于200的，那么由于b_(_i+_1_)" role="presentation" style="position: relative;">b_(_i+_1_)$\text{b\_(\_i+\_1\_)}$>,如果当 b_(_i+_1_)" role="presentation" style="position: relative;">b_(_i+_1_)$\text{b\_(\_i+\_1\_)}$->=256，则在高位上b_(_i+_1_)" role="presentation" style="position: relative;">b_(_i+_1_)$\text{b\_(\_i+\_1\_)}$

的对应权值一定大于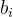在高位上对应的权值（我们这里的高位是指除了低8位以外的二进制位），由于a的值是小于200的，那么也就是说，a的高位上全为0，那么与b进行异或后高位上的值就是b数组高位上的值，那么如果  b_(_i+_1_)" role="presentation" style="position: relative;">b_(_i+_1_)$\text{b\_(\_i+\_1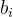\_)}$->=256，就有  b_(_i+_1_)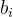" role="presentation" style="position: relative;">b_(_i+_1_)$\text{b\_(\_i+\_1\_)}$的高位大于的高位，那么一定不会有a_b_i" role="pre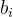sentation" style="position: relative;">a_b_i$\text{a\_b\_i}$^b_(_i+_1_)" role="presentation" style="position: relative;">b_(_i+_1_)$\text{b\_(\_i+\_1\_)}$<a_b_(i+1_)" role="presentation" style="position: relative;">a_b_(i+1_)$\text{a\_b\_(i+1\_)}$^成立，所以我们就可以直接排除掉，所以我们第二层for循环可以直接枚举256个，这样复杂度就变为O(256*n),这样就可以通过了

下面是代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=3e5+10;
int a[N],f[N];
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n;
		scanf("%d",&n);
		for(int i=0;i<n;i++)
		{
			scanf("%d",&a[i]);
			f[i]=1;
		}
		int mx=0;
		for(int i=0;i<n;i++)
		{
			for(int j=i+1;j<min(n,i+256);j++)
				if((a[i]^j)<(a[j]^i)) f[j]=max(f[j],f[i]+1);
			mx=max(mx,f[i]);
		}
		printf("%d\n",mx);
	}
	return 0;
}