• * 论文笔记【Neural Graph Collaborative Filtering】

    标题 * 表示未完成

    论文备份

    1. 研究目的
    • 本文指出无论是从早期的矩阵分解方式还是基于深度学习的方法，都需要编码后获得embedding，而只使用embedding的方法并不能很好的表达出 u s e r − i t e m user-item user−item的潜在交互关系，这种潜在关系在本文中被称为： c o l l a b o r a t i v e   s i g n a l collaborative \ signal collaborative signal，所以本文提出了 N e u r a l   G r a p h   C o l l a b o r a t i v e   F i l t e r i n g ( N G C F ) Neural\ Graph\ Collaborative\ Filtering (NGCF) Neural Graph Collaborative Filtering(NGCF) ，NGCF使用 bipartite graph structure 将 u s e r − i t e m user-item user−item的潜在交互关系更具体地集成到embedding过程中。
    1. 现有方法（研究现状）
    • c o l l a b o r a t i v e   d e e p   l e a r n i n g collaborative\ deep\ learning collaborative deep learning 通过学习 i t e m item item的边缘信息而得到的深度表征强化了MF的embedding功能
    • n e u r a l   c o l l a b o r a t i v e   f i l t e r i n g neural\ collaborative\ filtering neural collaborative filtering 通过使用非线性神经网络代替了传统MF的内积计算方式
    • t r a n s l a t i o n − b a s e d   C F   m o d e l s translation-based\ CF\ models translation−based CF models 采用欧氏距离度量作为交互函数
    • 本文指出在以往模型embedding时，通常只使用 u s e r − i t e m user-item user−item的ID和属性，而没有对 c o l l a b o r a t i v e   s i g n a l collaborative \ signal collaborative signal进行显式的编码，所以当embedding的关联信息不足时，只能使用更复杂的交互函数来弥补这一缺陷
    1. 本文模型及方法

    在这里插入图片描述
    上图为NGCF模型的架构图，此模型主要分为三个组成部分： e m b e d d i n g   l a y e r embedding\ layer embedding layer、 e m b e d d i n g   p r o p a g a t i o n   l a y e r s embedding\ propagation\ layers embedding propagation layers、 t h e   p r e d i c t i o n   l a y e r the\ prediction\ layer the prediction layer，下面会对这三个layer详细说明。

    • 对 c o l l a b o r a t i v e   s i g n a l collaborative \ signal collaborative signal显式编码是十分重要的，但如何对其编码是个麻烦的问题，本文提出了一种基于交互图结构的编码方式

    • c o l l a b o r a t i v e   s i g n a l collaborative \ signal collaborative signal
      传统MF建立embedding的方法并不能很好的表达出 u s e r − i t e m user-item user−item的潜在交互关系，这种潜在关系在本文中被称为： c o l l a b o r a t i v e   s i g n a l collaborative \ signal collaborative signal

    • h i g h − o r d e r   c o n n e c t i v i t y   A n d   u s e r − i t e m   i n t e r a c t i o n   g r a p h high-order\ connectivity\ And\ user-item\ interaction\ graph high−order connectivity And user−item interaction graph
      在这里插入图片描述
      分析上图，可以发现右图是以 u 1 u_1 u1​为根结点的树形结构展开，其中蕴含着丰富的信息，例如： u 2 ← i 2 ← u 1 u_2←i_2←u_1 u2​←i2​←u1​路径可以说明 u 1 u_1 u1​和 u 2 u_2 u2​具有一定的行为相似度； u 1 ← i 2 ← u 2 ← i 4 u_1 ← i_2 ← u_2 ← i_4 u1​←i2​←u2​←i4​路径可以说明 u 1 u_1 u1​除了对 i 2 i_2 i2​有兴趣，对 i 4 i_4 i4​也有兴趣；此外，当 l = 3 l=3 l=3时可以发现 i 4 i_4 i4​出现了两次而 i 5 i_5 i5​只出现了一次，所以用户 u 1 u_1 u1​可能对 i 4 i_4 i4​更感兴趣；当 l = 1 l=1 l=1时是目标用户直接交互过的 i t e m item item

    • E m b e d d i n g   L a y e r Embedding\ Layer Embedding Layer
      此layer建立 u s e r   e m b e d d i n g s   a n d   i t e m   e m b e d d i n g s user\ embeddings\ and\ item\ embeddings user embeddings and item embeddings的初始化状态
      在这里插入图片描述
      传统的MF以及NCF方法将上述 E E E 直接输入交互层进行分析，而本文的NGCF将上述 E E E 在 u s e r − i t e m   i n t e r a c t i o n   g r a p h user-item\ interaction\ graph user−item interaction graph上进行传播从而精炼embeddings

    • E m b e d d i n g   P r o p a g a t i o n   L a y e r s Embedding\ Propagation\ Layers Embedding Propagation Layers
      全文的精华都在这里了。
      这一层的思想即是精炼embeddings， 包括两个步骤，Message construction和Message aggregation
      （1） M e s s a g e   c o n s t r u c t i o n Message\ construction Message construction
      本文提出对于每一对 u s e r − i t e m user-item user−item的信息传递都可由以下公式定义(图示为从某一item到user)， f ( ⋅ ) f(⋅) f(⋅)表示 message encoding function， p u i p_{ui} pui​表示衰减系数，参考 Figure 1 h i g h − o r d e r   c o n n e c t i v i t y high-order\ connectivity high−order connectivity，我们可以自然的理解为从 i i i到 u u u的路径距离越远，那传播的效力就越低。 e i ( 0 )   e u ( 0 ) e_i^{(0)}\ e_u^{(0)} ei(0)​ eu(0)​的初始化值即使用传统的embeddings算法。
      在这里插入图片描述
      对于 f ( ⋅ ) f(⋅) f(⋅)本文更加具体的定义如下所示，⊙表示逐元素乘法，它是描述特征交互的一种经典方式。 p u i = 1 ∣ N u ∣ ∣ N i ∣ p_{ui} = \frac{1}{\sqrt {|N_u ||N_i|}} pui​=∣Nu​∣∣Ni​∣ ​1​ 其中 N u N_u Nu​表示的是与当前 u s e r user user直接有关联的（即本文所说的 first-hop neighbors）结点，如对于上图 Figure 中的 u 1 u_1 u1​与之直接有历史互动的的 i t e m item item，所以 p u i p_{ui} pui​表示过去访问过的 i t e m item item对于确认 u s e r user user偏好的贡献。（由于此传播算法是需要递归的，所以我们总结一下表达式可以看出多个 p u i p_{ui} pui​相乘肯定会使式子最后的计算结果越来越小，恰好满足了我们“离得越远 关联越少”的原则）
      在这里插入图片描述

    （2） M e s s a g e   A g g r e g a t i o n Message\ Aggregation Message Aggregation
    如下为本文提出 aggregation function，Leaky在本博客末尾有说明。
    其中 m u ← u = W 1 e u m_{u\gets{u}}=W_1e_u mu←u​=W1​eu​,此处的 W 1 W_1 W1​与上式（3）中的 W 1 W_1 W1​为同一个。其表示 self-connection。
    可以发现我们主要在向 u u u的“邻居”收集信息以获取更详细的embedding。
    在这里插入图片描述
    将其进一步多层迭代化表示如下。
    l l l 表示embedding传播层次，由于是递归，算法探索层次从高到低，再由低到高返回计算值。不要将 l l l 的定义和 N − h o p   n e i g h b o r s N-hop\ neighbors N−hop neighbors弄混淆。
    在这里插入图片描述
    在这里插入图片描述
    传播过程图如下配合着看会明了很多，注意图中的红线，可以发现 e u 1 ( 3 ) e^{(3)}_{u_1} eu1​(3)​中包含着离他最远的结点之一 e i 4 ( 0 ) e^{(0)}_{i_4} ei4​(0)​的信息，达到了目的。
    在这里插入图片描述
    （3） P r o p a g a t i o n   R u l e   i n   M a t r i x   F o r m Propagation\ Rule\ in\ Matrix\ Form Propagation Rule in Matrix Form
    更进一步的，文章提出了以上传播算法的矩阵表示形式。 L L L作者在文中表示相当于 p u i p_{ui} pui​， σ σ σ表示激活函数 L e a k y R e L U LeakyReLU LeakyReLU， I I I表示单位矩阵。此表达式把 u s e r , i t e m user, item user,item的 embeddings 矩阵结合起来使用递归进行传播计算。
    在这里插入图片描述
    这一段委实没有看明白，线性代数和矩阵分析课程的知识有所欠缺，补完之后再来看看。
    在这里插入图片描述

    • P r e d i c t i o n   L a y e r Prediction\ Layer Prediction Layer
      在文章中最终的 embeddings 是将所有的经过 E m b e d d i n g   P r o p a g a t i o n   L a y e r s Embedding\ Propagation\ Layers Embedding Propagation Layers构建出的 embedding 放在一起进行一个 concat 运算的结果。
      此处文章指出可以使用其他的方式整合数据，如 w e i g h t e d   a v e r a g e , m a x   p o o l i n g , L S T M weighted\ average, max\ pooling, LSTM weighted average,max pooling,LSTM等，但使用 concat 运算实现起来非常简单而且在图神经网络中有着很好的效果。
      在这里插入图片描述
      最后使用点乘来预测用户喜好
      在这里插入图片描述
      文章中优化器选用的是 p a i r w i s e   B P R   l o s s pairwise\ BPR\ loss pairwise BPR loss，并使用 m i n i − b a t c h   A d a m mini-batch\ Adam mini−batch Adam对模型进行优化并更新参数，使用 M e s s a g e   a n d   N o d e   D r o p o u t Message\ and\ Node\ Dropout Message and Node Dropout防止过拟合问题。
      在这里插入图片描述
      此文章的精华篇幅到这基本上结束了，之后就是一些综述，这里就不记录了。
    1. 实验结果
      NGCF模型的实验目标是回答以下问题：
      RQ 1：NGCF与目前最先进的CF方法相比表现如何？
      RQ 2：不同的超参数设置(例如，层的深度、嵌入传播层、层聚集机制，消息丢弃和结点丢弃)怎样影响着NGCF？
      RQ3：表示如何从高阶连通性中受益？
    • 以下模型为常用的CF模型，本文利用了 NGCF 与以下模型对比，说明NGCF的确优于常用的CF模型，本文也考虑了用SpectralCF 模型加入性能对比当中，但是发现特征分解导致高的时间成本和资源成本，特别是当用户和项目数量很大时性能特别差，但是在小型数据集中性能很好，所以没有选择它作为比较。为了公平的比较，所有的方法都优化了BPR损失（2.3所用的损失函数）结果如图。
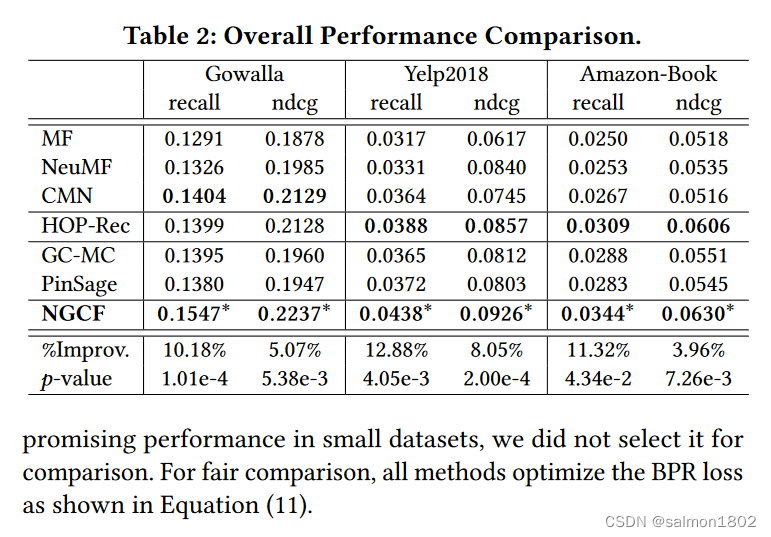
      在这里插入图片描述
    • 各个常用模型的性能表现对比
      NGCF和HOP-Rec在所有用户组上的表现始终优于所有其他模型。它证明了利用高阶连通性极大地促进了不活跃的用户模型学习性能，因为协同信号可以有效地被捕获，有希望解决推荐系统中的稀疏问题。
      在这里插入图片描述
    • 传播层层数的影响
      2层和3层的NGCF明显比1层的NGCF性能有所提高，这说明层数的加深对的确对提高NGCF的性能有所帮助，但是当上升到4层的时候，可以NGCF对Gowall数据集的recall和ndcg提升很多，但是其他数据集则相对降低，这说明当NGCF的嵌入传播层设置在4层的时候，NGCF产生了过拟合，所以NGCF嵌入传播层设置在三层的时候，对性能提升最大。
      在这里插入图片描述
    • 不同的聚集方法对NGCF的影响
      综合分析表2和表4，我们发现，当将各层的输出串联在一起时，NGCF-1PinSage和NGCF-1GC-MC的性能分别优于PinSage和GC-MC。这表明了层聚集机制的重要性。
      在这里插入图片描述
    1. 其它

    • L e a k y R e L U LeakyReLU LeakyReLU
      数学表达式：y = max(0, x) + leak*min(0,x) （leak是一个很小的常数，这样保留了一些负轴的值，使得负轴的信息不会全部丢失）
      在这里插入图片描述

    • 对于本文的 公式(3) 可以发现作者不仅考虑了message的来源 e i e_i ei​（传统图卷积方法只考虑这个），还考虑了信息来源和信息目的地之间的关系，即 e i ⊙ e u e_i ⊙ e_u ei​⊙eu​

    • L o n g   S h o r t   T e r m   M e m o r y   n e t w o r k s Long\ Short\ Term\ Memory\ networks Long Short Term Memory networks
      即LSTM，论文原文：正在架设传送门！

    • SVD（奇异值分解）
      相关介绍：正在架设传送门！

    • END

  • 相关阅读:
    深度学习-第T5周——运动鞋品牌识别
    用Three.js打造生成式NFT艺术藏品
    玩转UE4/UE5动画系统：UE5的运行时（动态）重定向治好了我的精神内耗
    make install在makefile的写法
    CSS便捷小工具
    华为机试真题 Java 实现【打印机队列】【2022.11 Q4 新题】
    湖南工商大学------函数及其应用
    预言机链上链下调研
    数据结构--二叉树
    MathJax公式编辑示例
  • 原文地址：https://blog.csdn.net/Salmon1122/article/details/126756886