论文阅读 (71)：Optimal Margin Distribution Machine for Multi-Instance Learning

1 概述

1.1 题目

2021IJCAI：多示例学习优化间隔分布机 (Optimal margin distribution machine for multi-Instance learning)

1.2 摘要

最近的间隔理论研究表明，间隔分布 (Margin distribution) 对泛化能力的影响重于最小间隔 (Minimal margin)。受此启发，提出了多示例 (Multi-instance learning, MIL) 最优间隔分布机 (ODM)，其通过优化间隔分布来鉴别关键实例。进一步扩展随机加速镜像近似方法 (Stochastic accelerated mirror prox method) 来解决该公式化的极小极大问题。

1.3 Bib

@inproceedings{Zhang:2021:23832389,
author		=	{Teng Zhang and Hai Jin},
title		=	{Optimal margin distribution machine for multi-instance learning},
booktitle	=	{International Conference on International Joint Conferences on Artificial Intelligence},
pages		=	{2383--2389},
year		=	{2021}
url			=	{https://www.ijcai.org/proceedings/2020/0330.pdf}
}
1
2
3
4
5
6
7
8

2 基础知识

令$\mathcal{X}\subseteq {\mathbb{R}}^n$和 Y = { − 1 , 1 } \mathcal{Y}=\{-1,1\} Y={−1,1}分别表示输入和输出空间。对于任意的$m\le 1$，整数的集合 { 1 , … , m } \{1,\dots,m\} {1,…,m}表示为$[m]$。与某个正定核$\kappa$关联的特征映射表示为：$\varphi :\mathcal{X}\to \mathbb{H}$。

2.1 ODM

定义有标记实例$(\mathbf{x},y)$的间隔$\gamma (\mathbf{x},y)$为Sign决策值，即$\gamma (\mathbf{x},y)=y{\mathbf{w}}^T\varphi (\mathbf{x})$，其可以作为预测的置信度 (Confidence)。间隔越大，预测的标签也越可信。
众所周知，SVM使用最大边界理论来描绘决策边界，所获得的分割超平面包含少量实例，也称支持向量，余下的实例则是可以忽略的。当噪声实例存在时，学习者可能被误导，从而产生次优决策边界。
与此相应，优化间隔分布是一个更健壮性的策略，其通过探索整个数据集来防止噪声实例的干扰。描述间隔分布最简单的方法是通过第一和第二统计，即间隔均值和方差。此外，同时最大化均值和最小化方差可以产生更严格的泛化边界。优化间隔分布机 (Optimal margin distribution machine, ODM) 被初定义为😮‍：
min ⁡ w , γ ‾ , ξ i , ϵ i 1 2 ∥ w ∥ 2 − η γ ‾ + λ m ∑ i ∈ [ m ] ( ξ i 2 + ϵ i 2 ) ,  s.t. γ ( x i , y i ) ≥ γ ‾ − ξ i , γ ( x i , y i ) ≤ γ ‾ + ϵ i , ∀ i ∈ [ m ] , (1) \tag{1}

minw,γ​,ξi​,ϵi​​ s.t.​21​∥w∥2−ηγ​+mλ​∑i∈[m]​(ξi2​+ϵi2​),γ(xi​,yi​)≥γ​−ξi​,γ(xi​,yi​)≤γ​+ϵi​,∀i∈[m],​(1)其中$\eta$喝$\lambda$是正则权衡参数，$\overline{\gamma }$是间隔均值，以及${\xi }_i$和${ϵ}_i$是$\gamma (\mathbf{x},y)$和间隔均值之间的偏差，因此公式1中的最后一项${\sum }_{i\in [m]}({\xi }_i^2+{ϵ}_i^2)/m$其实是间隔方差。
为了使得模型清晰有效，ODM被引入了三个改进：

1. 固定间隔均值；
2. 不同的偏差分配不同的权重；
3. 允许偏差小于给定阈值$\theta$以获取稀疏解。具体如下：

min ⁡ w , ξ i , ϵ i F ( w ) = 1 2 ∥ w ∥ 2 + λ m ∑ i ∈ [ m ] ξ i 2 + ν ϵ i 2 ( 1 − θ ) 2 ,  s.t.  y i w T ϕ ( x i ) ≥ 1 − θ − ξ i , y i w T ϕ ( x i ) ≤ 1 + θ + ϵ i , ∀ i ∈ [ m ] . (2) \tag{2}

minw,ξi​,ϵi​​ s.t. ​F(w)=21​∥w∥2+mλ​∑i∈[m]​(1−θ)2ξi2​+νϵi2​​,yi​wTϕ(xi​)≥1−θ−ξi​,yi​wTϕ(xi​)≤1+θ+ϵi​,∀i∈[m].​(2)其中$v$是不同偏差的权衡参数，以及$(1-\theta {)}^2$用于缩放第二项的替代损失。

3 方法

给定包含$m$个的训练集 S = { B i , y i } i ∈ [ m ] \mathcal{S}=\{\mathcal{B}_i,y_i\}_{i\in[m]} S={Bi​,yi​}i∈[m]​，其中 B i = { x i , 1 , … , x i , m i } \mathcal{B}_i=\{\boldsymbol{x}_{i,1},\dots,\boldsymbol{x}_{i,m_i}\} Bi​={xi,1​,…,xi,mi​​}是第$i$个包、 y i ∈ { ± 1 } y_i\in\{\pm1\} yi​∈{±1}是包标签，以及$m_i$是包中实例的数量。在不失一般性的前提下，假设前$p$个是正包，余下$m-p$是负包，即所有包可以被排序为：
y i = { 1 , i ∈ [ p ] , − 1 , i ∈ [ m ] ∖ [ p ] . y_i=\left\{

\right. yi​={1,−1,​i∈[p],i∈[m]∖[p].​包的标签预测由其实例的最大决策值决定，即$f({\mathcal{B}}_i)={\max }_{j\in [m_i]}{\mathbf{w}}^T\varphi ({\mathbf{x}}_{i,j})$。代入公式2有：
min ⁡ w , ξ i , ϵ i 1 2 ∥ w ∥ 2 + λ 1 p ∑ i = 1 p ξ i 2 + ν ϵ i 2 ( 1 − θ ) 2 + λ 2 q ∑ i = p + 1 m ξ i 2 + ν ϵ i 2 ( 1 − θ ) 2 ,  s.t.  y i max ⁡ j ∈ [ m i ] w T ϕ ( x i , j ) ≥ 1 − θ − ξ i , y i max ⁡ j ∈ [ m i ] w T ϕ ( x i , j ) ≤ 1 + θ + ϵ i , ∀ i ∈ [ m ] , (3) \tag{3}

minw,ξi,ϵi12‖w‖2+λ1p∑i=1pξi2+νϵi2(1−θ)2+λ2q∑i=p+1mξi2+νϵi2(1−θ)2, s.t. yimaxj∈[mi]wTϕ(xi,j)≥1−θ−ξi,yimaxj∈[mi]wTϕ(xi,j)≤1+θ+ϵi,∀i∈[m]," role="presentation" style="position: relative;">minw,ξi,ϵi s.t. 12∥w∥2+λ1p∑pi=1ξ2i+νϵ2i(1−θ)2+λ2q∑mi=p+1ξ2i+νϵ2i(1−θ)2,yimaxj∈[mi]wTϕ(xi,j)≥1−θ−ξi,yimaxj∈[mi]wTϕ(xi,j)≤1+θ+ϵi,∀i∈[m],$$\begin{array}{ll}\underset{\mathit{w},{\xi }_i,{ϵ}_i}{min}& \frac{1}{2}\Vert \mathit{w}{\Vert }^2+\frac{{\lambda }_1}{p}\sum _{i=1}^p\frac{{\xi }_i^2+\nu {ϵ}_i^2}{(1-\theta {)}^2}+\frac{{\lambda }_2}{q}\sum _{i=p+1}^m\frac{{\xi }_i^2+\nu {ϵ}_i^2}{(1-\theta {)}^2},\\ \text{ s.t. }& y_i\underset{j\in \left[m_i\right]}{max}{\mathit{w}}^T\varphi \left({\mathit{x}}_{i,j}\right)\ge 1-\theta -{\xi }_i,\\ & y_i\underset{j\in \left[m_i\right]}{max}{\mathit{w}}^T\varphi \left({\mathit{x}}_{i,j}\right)\le 1+\theta +{ϵ}_i,\mathrm{\forall }i\in [m],\end{array}$$

w,ξi​,ϵi​min​ s.t. ​21​∥w∥2+pλ1​​∑i=1p​(1−θ)2ξi2​+νϵi2​​+qλ2​​∑i=p+1m​(1−θ)2ξi2​+νϵi2​​,yi​maxj∈[mi​]​wTϕ(xi,j​)≥1−θ−ξi​,yi​maxj∈[mi​]​wTϕ(xi,j​)≤1+θ+ϵi​,∀i∈[m],​(3)其中${\lambda }_1$和${\lambda }_2$是权衡参数。
对于每一个正包${\mathcal{B}}_i$，引入二元向量：
a i = [ a i , 1 ; …   ; a i , m i ] ∈ { 0 , 1 } m i \boldsymbol{a}_i=[a_{i,1};\dots;a_{i,m_i}]\in\{0,1\}^{m_i} ai​=[ai,1​;…;ai,mi​​]∈{0,1}mi​来指示具有最大决策值的关键实例。依据标准多示例假设，每个正包中只有一个正实例，则有${\mathbf{e}}^T{\mathbf{a}}_i=1$，其中$\mathbf{e}$是一个全1向量。令$\mathbf{c}=[{\mathbf{a}}_1;\dots ,{\mathbf{a}}_p]$，以及$\mathcal{C}$表示其领域。然后公式3中的约束$y_i{\max }_{j\in \left[m_i\right]}{\mathbf{w}}^T\varphi \left({\mathbf{x}}_{i,j}\right)\ge 1-\theta -{\xi }_i$可以重写为${\max }_{{\mathbf{a}}_i}{\sum }_{j\in [m_i]}{a}_{i,j}{\mathbf{w}}^T\varphi ({\mathbf{x}}_{i,j})\ge 1-\theta -{\xi }_i$。
负包${\mathcal{B}}_i$中所有的实例都是负的，公式3与之相应的约束可以替换为：
{ − w T ϕ ( x i , j ) ≥ 1 − θ − ξ i , − w T ϕ ( x i , j ) ≤ 1 + θ + ϵ i , ∀ j ∈ [ m i ] . \left\{

−wTϕ(xi,j)≥1−θ−ξi,−wTϕ(xi,j)≤1+θ+ϵi,∀j∈[mi]." role="presentation" style="position: relative;">−wTϕ(xi,j)≥1−θ−ξi,−wTϕ(xi,j)≤1+θ+ϵi,∀j∈[mi].$$\begin{array}{l}-{\mathit{w}}^T\varphi ({\mathit{x}}_{i,j})\ge 1-\theta -{\xi }_i,\\ -{\mathit{w}}^T\varphi ({\mathit{x}}_{i,j})\le 1+\theta +{ϵ}_i,{\mathrm{\forall }}_j\in [m_i].\end{array}$$

\right. {−wTϕ(xi,j​)≥1−θ−ξi​,−wTϕ(xi,j​)≤1+θ+ϵi​,∀j​∈[mi​].​为了使得包更灵活，允许包有不同的松弛变量：
{ ξ s ( i , j ) } i ∈ [ m ] ∖ [ p ] , j ∈ [ m i ] , { ϵ s ( i , j ) } i ∈ [ m ] ∖ [ p ] , j ∈ [ m i ] , \{\xi_{s(i,j)}\}_{i\in[m]\setminus[p],j\in[m_i]},\qquad\{\epsilon_{s(i,j)}\}_{i\in[m]\setminus[p],j\in[m_i]}, {ξs(i,j)​}i∈[m]∖[p],j∈[mi​]​,{ϵs(i,j)​}i∈[m]∖[p],j∈[mi​]​,其中索引$s(i,j)=J_{i-1}-J_p+j+p$的范围为$p+1$到$J_m-J_p+p$，以及$J_i={\sum }_{t=1}^i{m}_t$ ($J_0=0$)。这个就是把所有的索$s(i,j)$重新索引至$p$到所有包的数量加$p$。结合以上，公式3转换为：
min ⁡ c ∈ C min ⁡ w , ξ i , ϵ i 1 2 ∥ w ∥ 2 + λ 1 p ∑ i = 1 p ξ i 2 + ν ϵ i 2 ( 1 − θ ) 2 + λ 2 q ∑ i = p + 1 m ∑ j ∈ [ m i ] ξ s ( i , j ) 2 + ν ϵ s ( i , j ) 2 ( 1 − θ ) 2 ,  s.t.  ∑ j ∈ [ m i ] a i , j w T ϕ ( x i , j ) ≥ 1 − θ − ξ i , ∑ j ∈ [ m i ] a i , j w T ϕ ( x i , j ) ≤ 1 + θ + ϵ i , ∀ i ∈ [ p ] , − w T ϕ ( x i , j ) ≥ 1 − θ − ξ s ( i , j ) , − w T ϕ ( x i , j ) ≤ 1 + θ + ϵ s ( i , j ) , ∀ i ∈ [ m ] \ [ p ] , ∀ j ∈ [ m i ] . (4) \tag{4}

minc∈Cminw,ξi,ϵi12‖w‖2+λ1p∑i=1pξi2+νϵi2(1−θ)2+λ2q∑i=p+1m∑j∈[mi]ξs(i,j)2+νϵs(i,j)2(1−θ)2, s.t. ∑j∈[mi]ai,jwTϕ(xi,j)≥1−θ−ξi,∑j∈[mi]ai,jwTϕ(xi,j)≤1+θ+ϵi,∀i∈[p],−wTϕ(xi,j)≥1−θ−ξs(i,j),−wTϕ(xi,j)≤1+θ+ϵs(i,j),∀i∈[m]∖[p],∀j∈[mi]." role="presentation" style="position: relative;">minc∈C s.t. minw,ξi,ϵi12∥w∥2+λ1p∑pi=1ξ2i+νϵ2i(1−θ)2+λ2q∑mi=p+1∑j∈[mi]ξ2s(i,j)+νϵ2s(i,j)(1−θ)2,∑j∈[mi]ai,jwTϕ(xi,j)≥1−θ−ξi,∑j∈[mi]ai,jwTϕ(xi,j)≤1+θ+ϵi,∀i∈[p],−wTϕ(xi,j)≥1−θ−ξs(i,j),−wTϕ(xi,j)≤1+θ+ϵs(i,j),∀i∈[m]∖[p],∀j∈[mi].$$\begin{array}{ll}\underset{\mathit{c}\in \mathcal{C}}{min}& \underset{\mathit{w},{\xi }_i,{ϵ}_i}{min}\frac{1}{2}\Vert \mathit{w}{\Vert }^2+\frac{{\lambda }_1}{p}\sum _{i=1}^p\frac{{\xi }_i^2+\nu {ϵ}_i^2}{(1-\theta {)}^2}\\ & +\frac{{\lambda }_2}{q}\sum _{i=p+1}^m\sum _{j\in \left[m_i\right]}\frac{{\xi }_{s(i,j)}^2+\nu {ϵ}_{s(i,j)}^2}{(1-\theta {)}^2},\\ \text{ s.t. }& \sum _{j\in \left[m_i\right]}{a}_{i,j}{\mathit{w}}^T\varphi \left({\mathit{x}}_{i,j}\right)\ge 1-\theta -{\xi }_i,\\ & \sum _{j\in \left[m_i\right]}{a}_{i,j}{\mathit{w}}^T\varphi \left({\mathit{x}}_{i,j}\right)\le 1+\theta +{ϵ}_i,\mathrm{\forall }i\in [p],\\ & -{\mathit{w}}^T\varphi \left({\mathit{x}}_{i,j}\right)\ge 1-\theta -{\xi }_{s(i,j)},\\ & -{\mathit{w}}^T\varphi \left({\mathit{x}}_{i,j}\right)\le 1+\theta +{ϵ}_{s(i,j)},\\ & \mathrm{\forall }i\in [m]\mathrm{\setminus }[p],\mathrm{\forall }j\in \left[m_i\right].\end{array}$$

minc∈C​ s.t. ​minw,ξi​,ϵi​​21​∥w∥2+pλ1​​∑i=1p​(1−θ)2ξi2​+νϵi2​​+qλ2​​∑i=p+1m​∑j∈[mi​]​(1−θ)2ξs(i,j)2​+νϵs(i,j)2​​,∑j∈[mi​]​ai,j​wTϕ(xi,j​)≥1−θ−ξi​,∑j∈[mi​]​ai,j​wTϕ(xi,j​)≤1+θ+ϵi​,∀i∈[p],−wTϕ(xi,j​)≥1−θ−ξs(i,j)​,−wTϕ(xi,j​)≤1+θ+ϵs(i,j)​,∀i∈[m]\[p],∀j∈[mi​].​(4)作为核方法，由于潜在的无限维特征映射，通常通过对偶形式处理公式4的内部最小化。引入对偶变量$\mathbf{u}=\left[u_1;\dots ;u_2\left(J_m-J_p+p\right)\right]⪰0$，公式4的拉格朗日形式为：
min ⁡ c ∈ C max ⁡ u ∈ U − 1 2 u T [ K − K − K K ] u − ( 1 − θ ) 2 4 u T [ 1 λ 1 I 0 0 1 λ 2 ν I ] u − [ ( θ − 1 ) e ( θ + 1 ) e ] T u (5) \tag{5}

minc∈Cmaxu∈U−12uT[K−K−KK]u−(1−θ)24uT[1λ1I001λ2νI]u−[(θ−1)e(θ+1)e]Tu" role="presentation" style="position: relative;">minc∈Cmaxu∈U−12uT[K−K−KK]u−(1−θ)24uT[1λ1I001λ2νI]u−[(θ−1)e(θ+1)e]Tu$$\begin{array}{rl}& \underset{\mathit{c}\in \mathcal{C}}{min}\underset{\mathit{u}\in \mathcal{U}}{max}-\frac{1}{2}{\mathit{u}}^T\left[\begin{array}{cc}\mathbf{K}& -\mathbf{K}\\ -\mathbf{K}& \mathbf{K}\end{array}\right]\mathit{u}\\ & -\frac{(1-\theta {)}^2}{4}{\mathit{u}}^T\left[\begin{array}{cc}\frac{1}{{\lambda }_1}\mathbf{I}& \mathbf{0}\\ \mathbf{0}& \frac{1}{{\lambda }_2\nu }\mathbf{I}\end{array}\right]\mathit{u}-{\left[\begin{array}{c}(\theta -1)\mathit{e}\\ (\theta +1)\mathit{e}\end{array}\right]}^T\mathit{u}\end{array}$$

​c∈Cmin​u∈Umax​−21​uT[K−K​−KK​]u−4(1−θ)2​uT[λ1​1​I0​0λ2​ν1​I​]u−[(θ−1)e(θ+1)e​]Tu​(5)其中$\mathcal{U}$是非负象限，以及${\mathbf{K}}_{i,j}={\mathbf{\Psi }}_i^{\top }{\mathbf{\Psi }}_j\in {\mathbb{R}}^{q\times q}$是带有
Ψ i = { ∑ j ∈ [ m i ] a i , j ϕ ( x i , j ) i ∈ [ p ] , j ∈ [ m i ] − ϕ ( x i , j ) i ∈ [ m ] \ [ p ] , j ∈ [ m i ] \boldsymbol{\Psi}_i=

{∑j∈[mi]ai,jϕ(xi,j)i∈[p],j∈[mi]−ϕ(xi,j)i∈[m]∖[p],j∈[mi]" role="presentation" style="position: relative;">{∑j∈[mi]ai,jϕ(xi,j)−ϕ(xi,j)i∈[p],j∈[mi]i∈[m]∖[p],j∈[mi]$$\{\begin{array}{ll}\sum _{j\in \left[m_i\right]}{a}_{i,j}\varphi \left({\mathit{x}}_{i,j}\right)& i\in [p],j\in \left[m_i\right]\\ -\varphi \left({\mathit{x}}_{i,j}\right)& i\in [m]\mathrm{\setminus }[p],j\in \left[m_i\right]\end{array}$$

Ψi​={∑j∈[mi​]​ai,j​ϕ(xi,j​)−ϕ(xi,j​)​i∈[p],j∈[mi​]i∈[m]\[p],j∈[mi​]​的核矩阵。
为了克服混合整数规划的求解困难，一些凸松弛方法被使用，例如半正定规划松弛，以及最大松弛 (Minimax relaxation)。本文则使用后者。改变最大最小的顺序，有：
$$\underset{\mathbf{u}\in \mathcal{U}}{\max }\underset{\mathbf{c}\in \mathcal{C}}{\min }D(\mathbf{u},\mathbf{c}),$$其中$D(\mathbf{u},\mathbf{c})$是公式5中的优化目标。此外，通过重写内部优化，以上公式转换为：
$$\underset{\mathbf{u}\in \mathcal{U}}{\max }\underset{\mathbf{c}\in \mathcal{C}}{\min }d\text{s.t. }D(\mathbf{u},{\mathbf{c}}_k)\ge d,\forall {\mathbf{c}}_k\in \mathcal{C}.\text{\hspace{1em}(6)}$$进一步于内优化引入对偶变量$\mathbf{v}=\left[v_1;\dots ;v_{|\mathcal{C}|}\right]⪰0$，公式6的拉格朗日形式为：
$$\underset{\mathbf{v}⪰0}{\min }\underset{d}{\max }\left\{d+\sum _{k:{\mathbf{c}}_k\in \mathcal{C}}{v}_k\left(D\left(\mathbf{u},{\mathbf{c}}_k\right)-d\right)\right\}.$$设置$d$的derivative为$0$，有${\sum }_{k:c_k\in \mathcal{C}}{v}_k=1$，以及对偶问题转换为：
$$\underset{\mathbf{v}\in \mathcal{V}}{\min }\sum _{k:c_k\in \mathcal{C}}{v}_{k}D\left(\mathbf{u},{\mathbf{c}}_k\right),\text{\hspace{1em}(7)}$$其中$\mathcal{V}=\left\{\mathbf{v}\in {\mathbb{R}}_{+}^{|\mathcal{C}|}\mid e^{\top }\mathbf{v}=1\right\}$是${\mathbb{R}}^{|\mathcal{C}|}$上的单纯形 (Simplex)为了简洁，${\sum }_{k:{\mathbf{c}}_k\in \mathcal{C}}{v}_{k}D\left(\mathbf{u},{\mathbf{c}}_k\right)$表示为$G(\mathbf{u},\mathbf{v})$，代入公式7，有：
$$\underset{\mathbf{u}\in \mathcal{U}}{\max }\underset{\mathbf{v}\in \mathcal{V}}{\min }G(\mathbf{u},\mathbf{v}).$$$G(\mathbf{u},\mathbf{v})$是负正定象限函数的凸组合，因此$v$凸$u$凹，以及根据Siont最大理论，这里存在一个鞍点$\left({\mathbf{u}}^{\star },{\mathbf{v}}^{\star }\right)\in \mathcal{U}\times \mathcal{V}$使得：
min ⁡ v ∈ V max ⁡ u ∈ U G ( u , v ) ≤ max ⁡ u ∈ U G ( u , v ⋆ ) = G ( u ⋆ , v ⋆ ) = min ⁡ v ∈ V G ( u , v ⋆ ) ≤ max ⁡ u ∈ U min ⁡ v ∈ V G ( u , v ) . (8) \tag{8}

minv∈Vmaxu∈UG(u,v)≤maxu∈UG(u,v⋆)=G(u⋆,v⋆)=minv∈VG(u,v⋆)≤maxu∈Uminv∈VG(u,v)." role="presentation" style="position: relative;">minv∈Vmaxu∈UG(u,v)≤maxu∈UG(u,v⋆)=G(u⋆,v⋆)=minv∈VG(u,v⋆)≤maxu∈Uminv∈VG(u,v).$$\begin{array}{c}\underset{\mathit{v}\in \mathcal{V}}{min}\underset{\mathit{u}\in \mathcal{U}}{max}G(\mathit{u},\mathit{v})\le \underset{\mathit{u}\in \mathcal{U}}{max}G\left(\mathit{u},{\mathit{v}}^{\star }\right)=G\left({\mathit{u}}^{\star },{\mathit{v}}^{\star }\right)\\ =\underset{\mathit{v}\in \mathcal{V}}{min}G\left(\mathit{u},{\mathit{v}}^{\star }\right)\le \underset{\mathit{u}\in \mathcal{U}}{max}\underset{\mathit{v}\in \mathcal{V}}{min}G(\mathit{u},\mathit{v}).\end{array}$$

v∈Vmin​u∈Umax​G(u,v)≤u∈Umax​G(u,v⋆)=G(u⋆,v⋆)=v∈Vmin​G(u,v⋆)≤u∈Umax​v∈Vmin​G(u,v).​(8)结合最大不等式：
$$\underset{\mathbf{v}\in \mathcal{V}}{\min }\underset{\mathbf{u}\in \mathcal{U}}{\max }G(\mathbf{u},\mathbf{v})\le \underset{\mathbf{u}\in \mathcal{U}}{\max }\underset{\mathbf{v}\in \mathcal{V}}{\min }G(\mathbf{u},\mathbf{v}),$$因此MI-ODM制定为：
$$\underset{\mathbf{v}\in \mathcal{V}}{\min }\underset{\mathbf{u}\in \mathcal{U}}{\max }G(\mathbf{u},\mathbf{v}).\text{\hspace{1em}(9)}$$最优质为鞍点$\left({\mathbf{u}}^{\star },{\mathbf{v}}^{\star }\right)$。

4 优化

简要地介绍最大问题，并详述用于快速最优值求解的随机加速镜像近似方法。

4.1 最大问题

根据一阶凸性不等式，$G(\mathbf{u},\cdot )$和$G(\cdot ,\mathbf{v})$均为凸函数，对于任意的对$(\hat{\mathbf{u}},\hat{\mathbf{v}})\in \mathcal{U}\times \mathcal{V}$，有：
G ( u , v ^ ) − G ( u ^ , v ^ ) ≤ − ∂ u G ( u ^ , v ^ ) ⊤ ( u ^ − u ) , ∀ u ∈ U , G ( u ^ , v ^ ) − G ( u ^ , v ) ≤ ∂ v G ( u ^ , v ^ ) ⊤ ( v ^ − v ) , ∀ v ∈ V .

​G(u,v^)−G(u^,v^)≤−∂u​G(u^,v^)⊤(u^−u),∀u∈U,G(u^,v^)−G(u^,v)≤∂v​G(u^,v^)⊤(v^−v),∀v∈V.​叠加以上不等式，并增广$\mathbf{u}$和$\mathbf{v}$，有：
$$G(\mathbf{u},\hat{\mathbf{v}})-G(\hat{\mathbf{u}},\mathbf{v})\le g(\hat{\mathbf{w}}{)}^{\top }(\hat{\mathbf{w}}-\mathbf{w}),\forall \mathbf{u},\mathbf{v},\text{\hspace{1em}(10)}$$其中$\mathbf{w}=[\mathbf{u};\mathbf{v}]$，以及$g(\hat{\mathbf{w}})=\left[-{\partial }_{\mathbf{u}}G(\hat{\mathbf{w}});{\partial }_{\mathbf{v}}G(\hat{\mathbf{w}})\right]$。与一般的凸优化相比，$g(\hat{\mathbf{w}})$扮演着梯度的角色。因此对于任意的$\mathbf{u}$和$\mathbf{v}$，有：
$$\underset{\mathbf{u}\in \mathcal{U}}{\max }G(\mathbf{u},\hat{\mathbf{v}})-\underset{\mathbf{v}\in \mathcal{V}}{\min }G(\hat{\mathbf{u}},\mathbf{v})\le g(\hat{\mathbf{w}}{)}^{\top }(\hat{\mathbf{w}}-\mathbf{w}).\text{\hspace{1em}(11)}$$公式11的LHS可以进一步分解为当前点$G(\hat{\mathbf{u}},\hat{\mathbf{v}})$与鞍点$\left({\mathbf{u}}^{\star },{\mathbf{v}}^{\star }\right)$之间的间隔：
max ⁡ u ∈ U G ( u , v ^ ) − G ( u ⋆ , v ⋆ ) + G ( u ⋆ , v ⋆ ) − min ⁡ v ∈ V G ( u ^ , v ) = max ⁡ u ∈ U G ( u , v ^ ) − min ⁡ v ∈ V u ∈ U max ⁡ U G ( u , v ) ⏟ ≥ 0 + max ⁡ u ∈ U min ⁡ v ∈ V G ( u , v ) − min ⁡ v ∈ V G ( u ^ , v ) ⏟ ≥ 0 .

maxu∈UG(u,v^)−G(u⋆,v⋆)+G(u⋆,v⋆)−minv∈VG(u^,v)=maxu∈UG(u,v^)−minv∈Vu∈UmaxUG(u,v)⏟≥0+maxu∈Uminv∈VG(u,v)−minv∈VG(u^,v)⏟≥0." role="presentation">maxu∈UG(u,v^)−G(u⋆,v⋆)+G(u⋆,v⋆)−minv∈VG(u^,v)=maxu∈UG(u,v^)−minv∈Vu∈UmaxUG(u,v)≥0+maxu∈Uminv∈VG(u,v)−minv∈VG(u^,v)≥0.$$\begin{array}{rl}& \underset{\mathit{u}\in \mathcal{U}}{max}G(\mathit{u},\hat{\mathit{v}})-G\left({\mathit{u}}^{\star },{\mathit{v}}^{\star }\right)+G\left({\mathit{u}}^{\star },{\mathit{v}}^{\star }\right)-\underset{\mathit{v}\in \mathcal{V}}{min}G(\hat{\mathit{u}},\mathit{v})\\ & =\underset{\ge 0}{\underbrace{\underset{\mathit{u}\in \mathcal{U}}{max}G(\mathit{u},\hat{\mathit{v}})-\underset{\mathit{v}\in \mathcal{V}\mathit{u}\in \mathcal{U}}{min}\underset{\mathit{U}}{max}G(\mathit{u},\mathit{v})}}+\underset{\ge 0}{\underbrace{\underset{\mathit{u}\in \mathcal{U}}{max}\underset{\mathit{v}\in \mathcal{V}}{min}G(\mathit{u},\mathit{v})-\underset{\mathit{v}\in \mathcal{V}}{min}G(\hat{\mathit{u}},\mathit{v})}}.\end{array}$$

​u∈Umax​G(u,v^)−G(u⋆,v⋆)+G(u⋆,v⋆)−v∈Vmin​G(u^,v)=≥0 u∈Umax​G(u,v^)−v∈Vu∈Umin​Umax​G(u,v)​​+≥0 u∈Umax​v∈Vmin​G(u,v)−v∈Vmin​G(u^,v)​​.​两个间隔均非负，其值越小越接近鞍点。公式11的LHS可以看作是一般凸优化中的“对偶间隔”，并作为算法设计的停止标准。

4.2 随机加速镜像近似

$\mathbf{u}$和$\mathbf{v}$的可行域分别对应框约束和单纯形。镜像下降方法用于探索其结构信息。对于变量$\mathbf{u}$，欧式距离镜像图${\psi }_{\mathcal{U}}=\Vert \mathbf{u}{\Vert }_2^2/2$可以工作的很好，对于变量$\mathbf{v}$，负熵镜像图${\psi }_{\mathcal{V}}(\mathbf{v})={\sum }_k\log v_k$很适用，因为它可以使得时间复杂度与维度的依赖程度是对数的。
镜像下降方法在镜像映射引起的对偶空间中执行梯度下降。为了使得最大结构得以像一般优化问题那样容易处理，引入联合镜像图$\psi (\mathbf{w})=a{\psi }_{\mathcal{U}}(\mathbf{u})+b{\psi }_{\mathcal{V}}(\mathbf{v})$，其中$a=\sqrt{2}/\tau \sqrt{J_m-J_p+p}$，以及$b=1/\sqrt{\log |\mathcal{C}|}$。这表明$\nabla \psi \mathcal{U}(\mathbf{u})=\mathbf{u}$，以及$\nabla {\psi }_{\mathcal{V}}(\mathbf{v})=\log \mathbf{v}+\mathbf{e}$。结合在一起有$\nabla \psi (\mathbf{w})=[a\mathbf{u};b\log \mathbf{v}+b\mathbf{e}]$。
如图1所示，在第$t$次迭代中，首先将当前点${\mathbf{w}}_t=\left[{\mathbf{u}}_t;{\mathbf{v}}_t\right]$映射到对偶空间$\nabla \psi \left({\mathbf{w}}_t\right)=$ $\left[a{\mathbf{u}}_t;b\log {\mathbf{v}}_t+b\mathbf{e}\right]$并执行一次梯度下降
∇ ( w ^ t ) = ∇ ψ ( w t ) − η g ( w t ) = [ a u t + η ∂ u G ( u t , v t ) ; b log ⁡ v t + b e − η ∂ v G ( u t , v t ) ] ,

=​∇(w^t​)=∇ψ(wt​)−ηg(wt​)[aut​+η∂u​G(ut​,vt​);blogvt​+be−η∂v​G(ut​,vt​)],​其中$\eta$是步长大小，然后将$\nabla \psi \left({\hat{\mathbf{w}}}_t\right)$映射回最初的空间，即找到${\hat{\mathbf{w}}}_t=\left[{\hat{\mathbf{u}}}_t;{\hat{\mathbf{v}}}_t\right]$：
[ a u ^ t b log ⁡ v ^ t + b e ] = [ a u t + η ∂ u G ( u t , v t ) b log ⁡ v t + b e − η ∂ v G ( u t , v t ) ] , \left[

au^tblog⁡v^t+be" role="presentation" style="position: relative;">au^tblogv^t+be$$\begin{array}{c}a{\hat{\mathit{u}}}_t\\ b\log {\hat{\mathit{v}}}_t+b\mathit{e}\end{array}$$

\right]=\left[

aut+η∂uG(ut,vt)blog⁡vt+be−η∂vG(ut,vt)" role="presentation" style="position: relative;">aut+η∂uG(ut,vt)blogvt+be−η∂vG(ut,vt)$$\begin{array}{c}a{\mathit{u}}_t+\eta {\mathrm{\partial }}_{\mathit{u}}G\left({\mathit{u}}_t,{\mathit{v}}_t\right)\\ b\log {\mathit{v}}_t+b\mathit{e}-\eta {\mathrm{\partial }}_{\mathit{v}}G\left({\mathit{u}}_t,{\mathit{v}}_t\right)\end{array}$$

\right], [au^t​blogv^t​+be​]=[aut​+η∂u​G(ut​,vt​)blogvt​+be−η∂v​G(ut​,vt​)​],其表明${\hat{\mathbf{u}}}_t={\mathbf{u}}_t+\eta {\partial }_{\mathbf{u}}G\left({\mathbf{u}}_t,{\mathbf{v}}_t\right)/a$且${\hat{\mathbf{v}}}_t=$ ${\mathbf{v}}_t\exp \left(-\eta {\partial }_{\mathbf{v}}G\left({\mathbf{u}}_t,{\mathbf{v}}_t\right)/b\right)$。最后，基于镜像图中的Bregman距离执行映射$\left[{\hat{\mathbf{u}}}_t;{\hat{\mathbf{v}}}_t\right]$到$\mathcal{U}\times \mathcal{V}$。特别地，欧式距离镜像图使用常用的欧氏距离，负熵镜像图使用Kullback-Leible散度。这可以制定为以下子优化问题：
u t + 1 = arg min ⁡ u ∈ U ∥ u − u ^ t ∥ 2 2 , v t + 1 = arg min ⁡ v ∈ V v T log ⁡ v v ^ t .

ut+1=\argminu∈U‖u−u^t‖22,vt+1=\argminv∈VvTlog⁡vv^t." role="presentation" style="position: relative;">ut+1=vt+1=\argminu∈U∥u−u^t∥22,\argminv∈VvTlogvv^t.$$\begin{array}{rl}{\mathit{u}}_{t+1}=& {\text{argmin}}_{\mathit{u}\in \mathcal{U}}\Vert \mathit{u}-{\hat{\mathit{u}}}_t{\Vert }_2^2,\\ {\mathit{v}}_{t+1}=& {\text{argmin}}_{\mathit{v}\in \mathcal{V}}{\mathit{v}}^T\log \frac{\mathit{v}}{{\hat{\mathit{v}}}_t}.\end{array}$$

ut+1​=vt+1​=​u∈Uargmin​∥u−u^t​∥22​,v∈Vargmin​vTlogv^t​v​.​

图1：镜像下降的一个迭代

这两个子优化问题都有近似解，前者将${\hat{\mathbf{u}}}_t$映射到非负象限，因此 u t + 1 = max ⁡ { u ^ t , 0 } \boldsymbol{u}_{t+1}=\max\{\hat{u}_t,0\} ut+1​=max{u^t​,0}。后者中引入对偶变量$z$，则拉格朗日形式为：
$$\underset{z}{\max }\underset{\mathbf{v}}{\min }{\mathbf{v}}^T\log \left(\mathbf{v}/{\hat{v}}_t\right)+z\left({\mathbf{e}}^T\mathbf{v}-1\right).$$设置$v$的derivative为$0$，有$\log \left(\mathbf{v}/{\hat{\mathbf{v}}}_t\right)+\mathbf{e}+$ $z\mathbf{e}=0$，其表明${\mathbf{v}}_{t+1}={\hat{\mathbf{v}}}_t\exp (-1-z)$。注意${\mathbf{v}}_{t+1}$属于一个单纯形，因此$1={\mathbf{e}}^{\top }{\mathbf{v}}_{t+1}={\mathbf{e}}^{\top }{\hat{\mathbf{v}}}_t\exp (-1-z)={\Vert {\hat{\mathbf{v}}}_t\Vert }_1\exp (-1-z)$。代入到$\exp (-1-z)=1/{\Vert {\hat{v}}_t\Vert }_1$，得到近似解$v_{t+1}={\hat{v}}_t/{\Vert {\hat{v}}_t\Vert }_1$。

有了${\mathbf{y}}_{t+1}\triangleq \left[{\mathbf{u}}_{t+1};{\mathbf{v}}_{t+1}\right]$后，从${\mathbf{w}}_t$；当在对偶空间执行梯度下降时，使用${\mathbf{y}}_{t+1}$而非${\mathbf{w}}_t$。换言之，一个两步镜像下降方法在每次迭代中执行，其从同一点开始，但第二次使用的梯度在第一次的结束点进行评估。该过程已被证明有很好的收敛性。 图2展示了该方法的一次迭代。

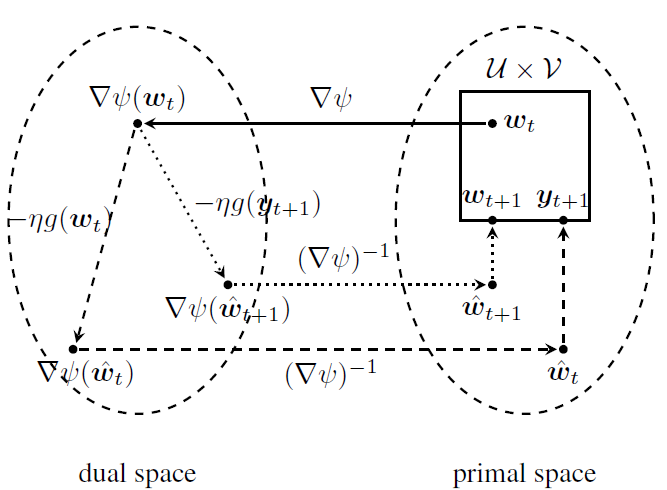
图2：镜像近似的一次迭代

镜像近似方法可以进一步通过Nesterov加速技术提速。方法是在 { w t } \left\{\boldsymbol{w}_t\right\} {wt​}和 { y t } \left\{\boldsymbol{y}_t\right\} {yt​}之外额外保留两个序列 { w ‾ t } \left\{\underline{\boldsymbol{w}}_t\right\} {w​t​}和 { w ‾ t } \left\{\overline{\boldsymbol{w}}_t\right\} {wt​}，其是 { w t } \left\{\boldsymbol{w}_t\right\} {wt​}和 { y t } \left\{\boldsymbol{y}_t\right\} {yt​}的结合。特别地，在第$t$次迭代中，首先更新${\underline{\mathbf{w}}}_t=\left(1-{\gamma }_t\right){\bar{\mathbf{w}}}_t+{\gamma }_t{\mathbf{y}}_t$，其中${\gamma }_t$是Nesterov加速系数，通常设置为$2/(t+1)$。随后，两部镜像近似基于${\underline{\mathbf{w}}}_t$来获得${\mathbf{y}}_{t+1}$和${\mathbf{w}}_{t+1}$。此外，为了使得数据集更好的适应大数据，该方法被扩展为一个随机版本，关键问题转换为找到无偏梯度${\partial }_{\mathbf{u}}\tilde{G}\left({\mathbf{u}}_t,{\mathbf{v}}_t\right)$和${\partial }_{\mathbf{v}}\tilde{G}\left({\mathbf{u}}_t,{\mathbf{v}}_t\right)$。注意$G(\mathbf{u},\mathbf{v})=$ ${\sum }_{k:c_k\in \mathcal{C}}{v}_{k}D\left(\mathbf{u},{\mathbf{c}}_k\right)$，则有
∂ u G ( u t , v t ) = [ ∂ u D ( u t , c 1 ) , … , ∂ u D ( u t , c ∣ C ∣ ) ] v t ∂ v G ( u t , v t ) = [ D ( u t , c 1 ) , … , D ( u t , c ∣ C ∣ ) ] .

​∂u​G(ut​,vt​)=[∂u​D(ut​,c1​),…,∂u​D(ut​,c∣C∣​)]vt​∂v​G(ut​,vt​)=[D(ut​,c1​),…,D(ut​,c∣C∣​)].​随机采样的索引$i_t$基于${\mathbf{v}}_t$在 { 1 , 2 , … , ∣ C ∣ } \{1,2, \ldots,|\mathcal{C}|\} {1,2,…,∣C∣}的分布获得，有${\partial }_{\mathbf{u}}\tilde{G}\left({\mathbf{u}}_t,{\mathbf{v}}_t,i_t\right)=$ ${\partial }_{\mathbf{u}}D\left({\mathbf{u}}_t,{\mathbf{c}}_{i_t}\right)$. 另一方面，均匀采样的索引$j_t$来自 { 1 , 2 , … , ∣ C ∣ } \{1,2, \ldots,|\mathcal{C}|\} {1,2,…,∣C∣}，有${\partial }_{\mathbf{v}}\tilde{G}\left({\mathbf{u}}_t,{\mathbf{v}}_t,j_t\right)=$ $\left[0,\dots ,|\mathcal{C}|D\left({\mathbf{u}}_t,{\mathbf{c}}_{j_t}\right)\dots ,0\right]$。这可以表示为：
E [ ∂ u G ~ ( u t , v t , i t ) ∣ u t , v t ] = ∂ u G ( u t , v t ) , E [ ∂ v G ~ ( u t , v t , j t ) ∣ u t , v t ] = ∂ v G ( u t , v t ) ,

E[∂uG~(ut,vt,it)∣ut,vt]=∂uG(ut,vt),E[∂vG~(ut,vt,jt)∣ut,vt]=∂vG(ut,vt)," role="presentation" style="position: relative;">E[∂uG˜(ut,vt,it)∣ut,vt]E[∂vG˜(ut,vt,jt)∣ut,vt]=∂uG(ut,vt),=∂vG(ut,vt),$$\begin{array}{rl}\mathbb{E}\left[{\mathrm{\partial }}_{\mathit{u}}\tilde{G}\left({\mathit{u}}_t,{\mathit{v}}_t,i_t\right)\mid {\mathit{u}}_t,{\mathit{v}}_t\right]& ={\mathrm{\partial }}_{\mathit{u}}G\left({\mathit{u}}_t,{\mathit{v}}_t\right),\\ \mathbb{E}\left[{\mathrm{\partial }}_{\mathit{v}}\tilde{G}\left({\mathit{u}}_t,{\mathit{v}}_t,j_t\right)\mid {\mathit{u}}_t,{\mathit{v}}_t\right]& ={\mathrm{\partial }}_{\mathit{v}}G\left({\mathit{u}}_t,{\mathit{v}}_t\right),\end{array}$$

E[∂u​G (ut​,vt​,it​)∣ut​,vt​]E[∂v​G (ut​,vt​,jt​)∣ut​,vt​]​=∂u​G(ut​,vt​),=∂v​G(ut​,vt​),​以及$\tilde{g}\left({\mathbf{w}}_t\right)=\left[-{\partial }_u\tilde{G}\left({\mathbf{u}}_t,{\mathbf{v}}_t,i_t\right);{\partial }_{\mathbf{v}}\tilde{G}\left({\mathbf{u}}_t,{\mathbf{v}}_t,j_t\right)\right]$是$g\left({\mathbf{w}}_t\right)$的期望无偏估计。
综合以上步骤，将获得随机加速镜像近似方法MI-ODM，如算法1。