吴恩达学习笔记（五）——优化算法

一、mini_batch梯度下降法

如果使用batch梯度下降法，mini-batch的大小为m，每个迭代需要处理大量的训练样本，弊端在于巡林样本巨大的时候，单次迭代耗时过长。

如果使用随机梯度下降法（mini-batch为1），只处理一个样本，通过减小学习率，噪声得到改善或者减小。缺点是失去向量化带来的加速，效率低下。且永远不会收敛，会一直在最小值附近波动，并不会达到最小值并停留在此。

所以实践中，通常选择不大不小的mini-batch尺寸。一方面，得到了大量向量化，比一次性处理多个样本快得多。另一方面，不需要等待整个训练集被处理完就可以开始后续工作。mini-batch梯度下降法不会总朝向最小值靠近，但比随机梯度下降更持续的靠近最小值的方向，也不一定在很小的范围内收敛或波动，如果出现这个问题，可以慢慢减少学习率。

mini-batch的选取指导原则：

如果训练集较小，直接使用batch梯度下降法，比如少于2000个样本；
样本数目较大的话，一般的mini-batch大小设置为64到512。考虑到电脑内存设置和使用的方式，mini-batch大小为2的n次方，代码运行的会快一些。

二、指数加权平均数

指数加权移动平均(Exponentially Weighted Moving Average)，他是一种常用的序列处理方式。在 $t$ 时刻，他的移动平均值公式是： $V_{t}=\beta V_{t-1}+(1-\beta) \theta_{t}$ ， $t = 1, 2, 3, ... n$ ，其中 $V_{t}$ 是 $t$ 时刻的移动平均预测值； $\theta_{t}$ 为 $t$ 时刻的真实值； $\beta$ 是权重；

以下该链接有β与平均多少天之间的关系：
参考链接

偏差修正：

在估测初期，不用 $v_{t}$ ，而是用 $\frac{v_{t}}{1-\beta _{t}}$

但在机器学习中，大部分时候并不在乎执行偏差修正，熬过初始时期，继续计算。

三、动量梯度下降法（momentum)

在这里插入图片描述

对于梯度下降法，很可能会出现上图那样的情况，需要很多的计算步骤。这种上下的波动会减慢梯度下降法的速度，无法使用更大的学习率（否则摆动较大，紫色箭头)，就只能使用较小的学习率。但从横轴来说，希望加快学习，能够快速从左到右，移动到最小值。

动量梯度下降法的实现:
在这里插入图片描述

在这里插入图片描述
注：
1. $\beta$ 最常用的值是0.9，是很棒的鲁棒数。
2.关于偏差校正，一般也不会进行。因为10次迭代后，移动平均已经过了初始阶段。
3. $v_{dw}$ 是维数和 $d w$ , w相同的零矩阵。
4.有的资料会把后面的项 $1-\beta$ 删除，这导致的结果是：学习率 $\alpha$ 要根据 $\frac{1}{1-\beta}$ 相应变化。

四、RMSprop

RMSprop也可以加速梯度下降。

假设纵轴是b，横轴是W，虽然横轴方向在缓慢推进，但纵轴方向会有大幅度地摆动。RMSprop就能减缓b方向的学习，加快横轴的学习。

在这里插入图片描述

简单解释一下就是：db大，所以算得的Sab也大，b的更新式除以了一个较大的数，所以减缓了b的摆动。蓝色的前进曲线被压缩为绿色的：
在这里插入图片描述
注：如果 $S_{dw}$ 的平方根趋近于0，要确保算法不会除以0，所以就要在分母上加上一个很小很小的数 $\epsilon$ ，比如 $10^{-8}$ ，保证数值稳定。

五、Adam优化算法

结合了Momentum和RMSprop

在这里插入图片描述

超参数的选择（常用）：

$\beta _{1}$ ：0.9
$\beta _{2}$ ：0.999
$\epsilon$ ： $10^{-8}$

六、学习率衰减

加快学习算法的一个办法就是：随时间慢慢减少学习率。

蓝色线：使用mini-batch梯度下降法，在迭代过程中，存在着噪音，下降朝向最小值，但不会精确收敛，在附近摆动。这是因为用的 $\alpha$ 是固定值。

绿色线：但如果随着 $\alpha$ 变小，步伐也会变小，最后曲线会在最小值附近很小的一块区域内摆动。

在这里插入图片描述
拆分成不同的mini-batch，第一次遍历训练集叫做第一代。

其他的一些衰减方式：

1. $\alpha=0.95^{epoch-num}\alpha_{0}$
2. $\alpha=\frac{k}{\sqrt {epoch-num}} \alpha_{0}$ 或者 $\alpha=\frac{k}{\sqrt {t} }\alpha_{0}$ （t为mini-batch 的数字）
3.离散下降，一次减少一半。

七、局部最优的问题

通常梯度为0的点并不是图1中的局部最优点，实际上，成本函数的零梯度点，通常是鞍点。

在这里插入图片描述
图1

在这里插入图片描述
图2

即一个具有高维度空间的函数，如果梯度为0，在每个方向，它可能是凸函数，也可能是凹函数。因此吗，更可能碰到鞍点。

但平稳段是一个问题，这会使得学习十分缓慢，所以Mmomentum或者RMSprop、Adam才要加速学习算法。

八、编程作业

参考链接

opt_utils.py

import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets

def sigmoid(x):
    """
    Compute the sigmoid of x
 
    Arguments:
    x -- A scalar or numpy array of any size.
 
    Return:
    s -- sigmoid(x)
    """
    s = 1/(1+np.exp(-x))
    return s
 
def relu(x):
    """
    Compute the relu of x
 
    Arguments:
    x -- A scalar or numpy array of any size.
 
    Return:
    s -- relu(x)
    """
    s = np.maximum(0,x)
    
    return s


def load_params_and_grads(seed=1):
    np.random.seed(seed)
    W1 = np.random.randn(2,3)
    b1 = np.random.randn(2,1)
    W2 = np.random.randn(3,3)
    b2 = np.random.randn(3,1)
 
    dW1 = np.random.randn(2,3)
    db1 = np.random.randn(2,1)
    dW2 = np.random.randn(3,3)
    db2 = np.random.randn(3,1)
    
    return W1, b1, W2, b2, dW1, db1, dW2, db2
    
def initialize_parameters(layer_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the dimensions of each layer in our network
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
                    b1 -- bias vector of shape (layer_dims[l], 1)
                    Wl -- weight matrix of shape (layer_dims[l-1], layer_dims[l])
                    bl -- bias vector of shape (1, layer_dims[l])
                    
    Tips:
    - For example: the layer_dims for the "Planar Data classification model" would have been [2,2,1]. 
    This means W1's shape was (2,2), b1 was (1,2), W2 was (2,1) and b2 was (1,1). Now you have to generalize it!
    - In the for loop, use parameters['W' + str(l)] to access Wl, where l is the iterative integer.
    """
    
    np.random.seed(3)
    parameters = {}
    L = len(layer_dims) # number of layers in the network
 
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])*  np.sqrt(2 / layer_dims[l-1])
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
        
        assert(parameters['W' + str(l)].shape == layer_dims[l], layer_dims[l-1])
        assert(parameters['W' + str(l)].shape == layer_dims[l], 1)
        
    return parameters
    
def forward_propagation(X, parameters):
    """
    Implements the forward propagation (and computes the loss) presented in Figure 2.
    
    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
                    W1 -- weight matrix of shape ()
                    b1 -- bias vector of shape ()
                    W2 -- weight matrix of shape ()
                    b2 -- bias vector of shape ()
                    W3 -- weight matrix of shape ()
                    b3 -- bias vector of shape ()
    
    Returns:
    loss -- the loss function (vanilla logistic loss)
    """
    
    # retrieve parameters
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
    
    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    z1 = np.dot(W1, X) + b1
    a1 = relu(z1)
    z2 = np.dot(W2, a1) + b2
    a2 = relu(z2)
    z3 = np.dot(W3, a2) + b3
    a3 = sigmoid(z3)
    
    cache = (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3)
    
    return a3, cache
 
def backward_propagation(X, Y, cache):
    """
    Implement the backward propagation presented in figure 2.
    
    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat)
    cache -- cache output from forward_propagation()
    
    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """
    m = X.shape[1]
    (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3) = cache
    
    dz3 = 1./m * (a3 - Y)
    dW3 = np.dot(dz3, a2.T)
    db3 = np.sum(dz3, axis=1, keepdims = True)
    
    da2 = np.dot(W3.T, dz3)
    dz2 = np.multiply(da2, np.int64(a2 > 0))
    dW2 = np.dot(dz2, a1.T)
    db2 = np.sum(dz2, axis=1, keepdims = True)
    
    da1 = np.dot(W2.T, dz2)
    dz1 = np.multiply(da1, np.int64(a1 > 0))
    dW1 = np.dot(dz1, X.T)
    db1 = np.sum(dz1, axis=1, keepdims = True)
    
    gradients = {"dz3": dz3, "dW3": dW3, "db3": db3,
                 "da2": da2, "dz2": dz2, "dW2": dW2, "db2": db2,
                 "da1": da1, "dz1": dz1, "dW1": dW1, "db1": db1}
    
    return gradients
 
def compute_cost(a3, Y):
    
    """
    Implement the cost function
    
    Arguments:
    a3 -- post-activation, output of forward propagation
    Y -- "true" labels vector, same shape as a3
    
    Returns:
    cost - value of the cost function
    """
    m = Y.shape[1]
    
    logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
    cost = 1./m * np.sum(logprobs)
    
    return cost
 
def predict(X, y, parameters):
    """
    This function is used to predict the results of a  n-layer neural network.
    
    Arguments:
    X -- data set of examples you would like to label
    parameters -- parameters of the trained model
    
    Returns:
    p -- predictions for the given dataset X
    """
    
    m = X.shape[1]
    p = np.zeros((1,m), dtype = np.int)
    
    # Forward propagation
    a3, caches = forward_propagation(X, parameters)
    
    # convert probas to 0/1 predictions
    for i in range(0, a3.shape[1]):
        if a3[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0
 
    # print results
 
    #print ("predictions: " + str(p[0,:]))
    #print ("true labels: " + str(y[0,:]))
    print("Accuracy: "  + str(np.mean((p[0,:] == y[0,:]))))
    
    return p
 
def predict_dec(parameters, X):
    """
    Used for plotting decision boundary.
    
    Arguments:
    parameters -- python dictionary containing your parameters 
    X -- input data of size (m, K)
    
    Returns
    predictions -- vector of predictions of our model (red: 0 / blue: 1)
    """
    
    # Predict using forward propagation and a classification threshold of 0.5
    a3, cache = forward_propagation(X, parameters)
    predictions = (a3 > 0.5)
    return predictions
 
def plot_decision_boundary(model, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
    y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
    plt.show()
 
def load_dataset(is_plot = True):
    np.random.seed(3)
    train_X, train_Y = sklearn.datasets.make_moons(n_samples=300, noise=.2) #300 #0.2 
    # Visualize the data
    if is_plot:
        plt.scatter(train_X[:, 0], train_X[:, 1], c=train_Y, s=40, cmap=plt.cm.Spectral)
        plt.show()
    train_X = train_X.T
    train_Y = train_Y.reshape((1, train_Y.shape[0]))
    
    return train_X, train_Y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248

实现代码：

import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets

import opt_utils
import testCase

plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

# 梯度下降
def update_parameters_with_gd(parameters, grads, learning_rate):

    L = len(parameters) // 2

    for l in range(L):

        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]

    return parameters

# 实现mini-batch
def random_mini_batches(X, Y, mini_batch_size=64, seed=0):

    np.random.seed(seed)
    m = X.shape[1]
    mini_batches = []

    # 先打乱顺序
    permutation = list(np.random.permutation(m)) # #它会返回一个长度为m的随机数组，且里面的数是0到m-1;这里不用list也行
    shuffle_X = X[:, permutation]
    shuffle_Y = Y[:, permutation].reshape((1, m))

    # 分割
    num_complete_minibatches = math.floor(m / mini_batch_size) # 向下取整,一共分成了多少份

    for k in range(0, num_complete_minibatches):

        mini_batch_X = shuffle_X[:, k*mini_batch_size:(k+1) * mini_batch_size]
        mini_batch_Y = shuffle_Y[:, k * mini_batch_size:(k + 1) * mini_batch_size]

        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    # 处理没有被平分的剩余部分
    if m % mini_batch_size != 0:

        mini_batch_X = shuffle_X[:, num_complete_minibatches * mini_batch_size:]
        mini_batch_Y = shuffle_Y[:, num_complete_minibatches * mini_batch_size:]

        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    return mini_batches

# 初始化，包含动量的梯度下降,建立一个和dW、db相同结构的变量来影响他们
def initialize_velocity(parameters):

    L = len(parameters) // 2
    v = {}

    for l in range(L):

        v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])

    return v

# 实现动量梯度下降
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):

    L = len(parameters) // 2

    for l in range(L):

        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads["dW" + str(l + 1)]
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]

        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads["db" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]

    return parameters, v

# 初始化，Adam算法
def initialize_adam(parameters):

    L = len(parameters) // 2
    v = {}
    s = {}

    for l in range(L):

        v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])

        s["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        s["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])

    return (v, s)

# 实现Adam算法
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate=0.1, beta1=0.9, beta2=0.999, epsilon=1e-8):

    L = len(parameters) // 2
    v_corrected = {}
    s_corrected = {}

    for l in range(L):

        v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * grads["dW" + str(l + 1)]
        v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - np.power(beta1, t))
        s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * np.square(grads["dW" + str(l + 1)])
        s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2, t))
        # parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v_corrected["dW" + str(l + 1)] / (np.sqrt(s_corrected["dW" + str(l + 1)]) + epsilon)
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * (v_corrected["dW" + str(l + 1)] /
                    np.sqrt(s_corrected["dW" + str(l + 1)] + epsilon)) # 将epsilon写在根号里面

        v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads["db" + str(l + 1)]
        v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1, t))
        s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.square(grads["db" + str(l + 1)])
        s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2, t))
        # parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v_corrected["db" + str(l + 1)] / (np.sqrt(s_corrected["db" + str(l + 1)]) + epsilon)
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * (v_corrected["db" + str(l + 1)] /
            np.sqrt(s_corrected["db" + str(l + 1)] + epsilon))

    return (parameters, v, s)


# 测试
# 加载数据集
train_X, train_Y = opt_utils.load_dataset(is_plot=True)

# 定义模型
def model(X, Y, layers_dims, optimizer, learning_rate=0.0007, mini_batch_size=64, beta1=0.9, beta2=0.999, epsilon=1e-8, num_epochs=10000, print_cost=True, is_plot=True):

    L = len(layers_dims)
    costs = []
    t = 0 # 每学习一个mini-batch,t就加一
    seed = 10

    parameters = opt_utils.initialize_parameters(layers_dims)

    # 选择优化器
    if optimizer == "gd":
        pass
    elif optimizer == "momentum":
        v = initialize_velocity(parameters)
    elif optimizer == "adam":
        v, s = initialize_adam(parameters)
    else:
        print("optimizer参数错误，程序退出。")
        exit(1)

    for i in range(num_epochs):

        seed = seed + 1 # 每次遍历完数据集后，重新排列数据集
        minibatches = random_mini_batches(X, Y, mini_batch_size, seed)

        for minibatch in minibatches:

            (minibatch_X, minibatch_Y) = minibatch

            A3, cache = opt_utils.forward_propagation(minibatch_X, parameters)

            cost = opt_utils.compute_cost(A3, minibatch_Y)

            grads = opt_utils.backward_propagation(minibatch_X, minibatch_Y, cache)

            # 更新参数
            if optimizer == "gd":
                parameters = update_parameters_with_gd(parameters, grads, learning_rate)
            elif optimizer == "momentum":
                parameters, v = update_parameters_with_momentum(parameters, grads, v, beta1, learning_rate)
            elif optimizer == "adam":
                t = t + 1
                parameters, v, s = update_parameters_with_adam(parameters, grads, v, s, t, learning_rate, beta1, beta2, epsilon)

        if i % 100 == 0:
            costs.append(cost)
            if print_cost and i % 1000 == 0:
                print("第" + str(i) + "次遍历整个数据集，当前误差值：" + str(cost))

    if is_plot:
        plt.plot(costs)
        plt.ylabel('cost')
        plt.xlabel('epochs (per 100)')
        plt.title("Learning rate = " + str(learning_rate))
        plt.show()

    return parameters


layers_dims = [train_X.shape[0], 5, 2, 1]
# 使用普通的梯度下降
#parameters = model(train_X, train_Y, layers_dims, optimizer="gd",is_plot=True)
#使用动量的梯度下降
#parameters = model(train_X, train_Y, layers_dims, beta1=0.9, optimizer="momentum", is_plot=True)
#使用Adam优化的梯度下降
parameters = model(train_X, train_Y, layers_dims, optimizer="adam", is_plot=True)

#预测
preditions = opt_utils.predict(train_X,train_Y,parameters)

#绘制分类图
#plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214

8.1. 使用普通的梯度下降

在这里插入图片描述

震荡原因：每个子训练集收敛的方向不一定和总训练集收敛方向相同（有时候甚至相反），所以会震荡。但是因为训练总是遍历了总训练集，所以虽然震荡但还是向cost小的方向收敛

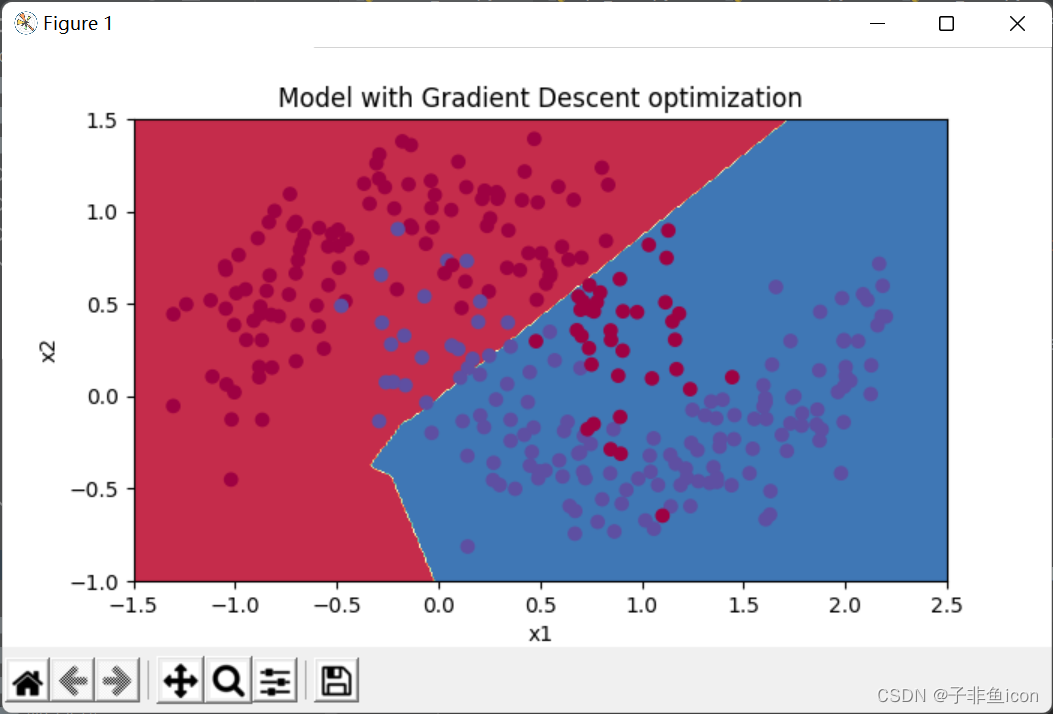
第0次遍历整个数据集，当前误差值：0.690735512291113
第1000次遍历整个数据集，当前误差值：0.6852725328458241
第2000次遍历整个数据集，当前误差值：0.6470722240719003
第3000次遍历整个数据集，当前误差值：0.6195245549970402
第4000次遍历整个数据集，当前误差值：0.5765844355950945
第5000次遍历整个数据集，当前误差值：0.6072426395968576
第6000次遍历整个数据集，当前误差值：0.5294033317684576
第7000次遍历整个数据集，当前误差值：0.46076823985930115
第8000次遍历整个数据集，当前误差值：0.465586082399045
第9000次遍历整个数据集，当前误差值：0.4645179722167684
Accuracy: 0.7966666666666666
1
2
3
4
5
6
7
8
9
10
11

8.2. 使用动量的梯度下降
在这里插入图片描述

第0次遍历整个数据集，当前误差值：0.6907412988351506
第1000次遍历整个数据集，当前误差值：0.6853405261267578
第2000次遍历整个数据集，当前误差值：0.6471448370095255
第3000次遍历整个数据集，当前误差值：0.6195943032076022
第4000次遍历整个数据集，当前误差值：0.5766650344073023
第5000次遍历整个数据集，当前误差值：0.607323821900647
第6000次遍历整个数据集，当前误差值：0.5294761758786997
第7000次遍历整个数据集，当前误差值：0.46093619004872366
第8000次遍历整个数据集，当前误差值：0.465780093701272
第9000次遍历整个数据集，当前误差值：0.4647395967922748
Accuracy: 0.7966666666666666
1
2
3
4
5
6
7
8
9
10
11

因为这个例子比较简单，使用动量效果很小，但对于更复杂的问题，会有更好的效果。

8.3. 使用Adam的梯度下降

在这里插入图片描述

第0次遍历整个数据集，当前误差值：0.6905522446113365
第1000次遍历整个数据集，当前误差值：0.18550136438550574
第2000次遍历整个数据集，当前误差值：0.15083046575253212
第3000次遍历整个数据集，当前误差值：0.07445438570997179
第4000次遍历整个数据集，当前误差值：0.1259591565133716
第5000次遍历整个数据集，当前误差值：0.10434443534245479
第6000次遍历整个数据集，当前误差值：0.10067637504120656
第7000次遍历整个数据集，当前误差值：0.0316520301351156
第8000次遍历整个数据集，当前误差值：0.11197273131244208
第9000次遍历整个数据集，当前误差值：0.19794007152465498
Accuracy: 0.94
1
2
3
4
5
6
7
8
9
10
11

在这里插入图片描述

具有动量的梯度下降通常可以有很好的效果，但由于小的学习速率和简单的数据集所以它的影响几乎是轻微的。另一方面，Adam明显优于小批量梯度下降和具有动量的梯度下降，如果在这个简单的模型上运行更多时间的数据集，这三种方法都会产生非常好的结果，然而，我们已经看到Adam收敛得更快。

np.random.permutation()函数

相关阅读:
计算机毕业设计SSM大学体育馆预约系统【附源码数据库】
高并发，不怕不怕「限流算法第一把法器：计数器法」
面试被吊打！正确打开Redis分布式锁的七种方案，涨见识了
pandas notes 25
elasticsearch的docker安装与使用
多叉树+图实现简单业务流程
Springboot建筑造价师资格考试应试网站毕业设计源码260839
小程序弹窗
gunicorn 支持如下4种工作模式，Gunicorn“绿色独角兽”
(免费分享)基于springboot健康运动-带论文

原文地址：https://blog.csdn.net/weixin_45719141/article/details/126686893