-
决策树笔记1
1.信息熵 熵越小集合纯度越高

样本集合中第K类样本所占比例
2.信息增益#ID3决策树的算法#加权

Dv:存在一特征a,取值集合为{a1,a2,a3,…aV};
存在一样本集合D;
用特征a对样本D进行划分,Dv就表示D样本中所有包含av特征的样本;
信息增益理解为整体样本的信息熵减去根据某一特征划分后对整体样本的信息熵。#理解为划分后的信息熵加上增益就是总体信息熵;如果划分后的信息熵越小#即信息增益越大,那么说明划分的效果纯度高,划分效果好。
3.增益率#C4.5决策树算法
argmax信息增益率存在一个问题,为了使划分属性的加权信息熵最小,推广至极端那么对每一个样本做一个分类纯度不就最大了,因此信息增益率最大化会偏向于那些划分属性多的特征。也就意味这泛化能力差#难以跑新样本。

C4.5使用信息增益率来解决上述问题,IV(属性a的intrinsic value),和划分特征的加权信息熵一个意思,gain_ratio = (ENT-IV)/IV;
C4.5算法从划分属性中找到信息增益高于平均水平的属性再选择增益率最高的。
4.基尼系数gini index#CART(classification and regression tree)
数据集合的GINI

从数据集中任选两个样本,样本类别不一致的概率,GINI越小,纯度越高。
特征a的GINI

剪枝(#处理过拟合)#Pruning
过拟合,决策树过度划分节点,以至于将数据样本的特点定性为整体数据的特点,表现为训练集效果好,测试集效果差。
剪枝分为:
预剪枝#prepruning
在划分节点前进行估计,评价这个节点带来的泛化性能提升,如果不达标就不划分,将这个节点编程叶子节点。
后剪枝#postpruning
跑完整个训练集后,从根节点开始,对每个节点下面一层的分支考虑如果这些分支变成叶子节点会不会是泛化性能提升,如果会就换成叶子节点。#泛化指标是测试集合上的误差#近似于泛化误差这里引出性能评估的方法 1.hold-out留出法#划分出两个互斥集合 2.交叉验证(cross validation)#数据集合划分为K个子集#尽量保证独立同分布,每次训练k-1个子集然后对哪一个子集测试,总共可以训练k次,结果使用K次训练结果均值。 3.自助法#bootstrap#考虑到切分样本带来的估计偏差#设数据集D有n个样本,放回抽样m次构成有m个样本的数据集D1;对一个样本来说,它被采集到的概率是1/m,所以样本在m次采样中始终不被采集到的概率是: 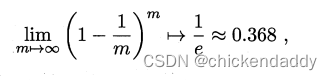 所以总体样本中有36.8%样本不被采集到,因此D1可以作为训练集,D作为测试集。#测试结果称为out-of-bag 4.调参 5.性能度量performance measure 均方误差 mean squared error# for regression problem 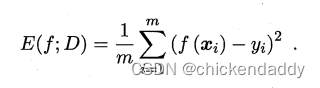 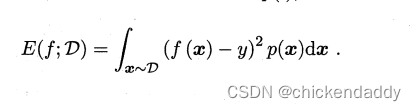 错误率 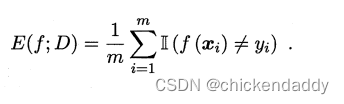 精度 accuracy 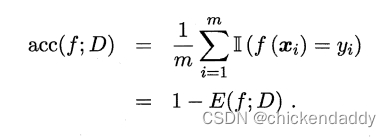 查准率precision  查全率 recall 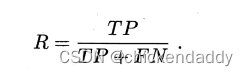 F1&Fb  ROC&AUC 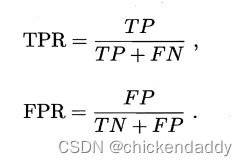 ROC的yaxis是TPR,xaxis是FPR- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
-
相关阅读:
小试从Intel MediaSDK迁移到OneVPL
【SpringBoot】自动装配原理
3D 生成重建007-Fantasia3D和Magic3d两阶段玩转文生3D
opencv项目9---利用YOLOv3实现对物体的实时检测
【数字图像处理】Gamma 变换
多层板交期怎么才能有效把控?
万字长文详解Webpack5高级优化
添加环境变量
mindspore-使用net(input)或者model.predict获取对应预测值,forward获取一次结果较慢
conda config包含无效channel解决办法
- 原文地址:https://blog.csdn.net/chickendaddy/article/details/126723183
