【题解笔记】PTA基础6-10：阶乘计算升级版

题目地址：https://pintia.cn/problem-sets/14/problems/742

前言#

咱目前还只能说是个小白，写题解是为了后面自己能够回顾。如果有哪些写错的/能优化的地方，也请各位多指教。( •̀ ω •́ )

题目描述#

本题要求实现一个打印非负整数阶乘的函数，要求能处理一定大数值的阶乘。

展开查看详情

函数接口定义#

void Print_Factorial ( const int N );

其中N是用户传入的参数，其值不超过1000。如果N是非负整数，则该函数必须在一行中打印出N!的值，否则打印"Invalid input"。

裁判测试程序样例#

#include 

void Print_Factorial ( const int N );

int main()
{
    int N;
    
    scanf("%d", &N);
    Print_Factorial(N);
    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例#

15

输出样例#

1307674368000

限制#

限制内容	限制条件
代码长度限制	16 KB
时间限制	400 ms
空间限制	64 MB

想法#

怎么储存如此之大的阶乘结果#

不看不知道，细看吓一跳，题目中对N的限制是0<=N<=1000，得想个办法让程序储存1000!这么大的一个数。

扫视了一圈C语言的基本数据类型，就连unsigned long long类型也远存不下1000的阶乘。

转换一下思路。数字每一位之间都是紧挨在一起的，我们其实可以采用一种连续的数据结构来储存这个结果，比如....数组！

设数组第一个元素表示个位，第二个元素表示十位...以此类推。这样一来，我们就可以用数组以数位升序来储存这个大数了。最后只需将数组中的每个元素(int)打印到屏幕上即可。

给数组分配多少个元素#

题目的裁判测试程序并没有引入stdlib.h头文件，因此我没法使用动态内存分配/回收函数。而1000!的结果到底有多少位，我一时半会儿也是不知道的。

其实可以用最简单粗暴的方式估计一下：1000个1000相乘

1×103×103⋯×103=1×103×1000" role="presentation">1×103×103⋯×103=1×103×1000$$1\times {10}^3\times {10}^3\cdots \times {10}^3=1\times {10}^{3\times 1000}$$

这样算出来的结果有3001位。如果是运算1000!的话，是怎么也不会算出3001个数位的数字的，所以分配3000个元素一定能保证数组能装得下结果的所有数位。

注：有一种可以用来计算阶乘近似值的公式——斯特林公式

实现乘法时关注的对象#

阶乘运算的基础是乘法运算，只要把正确的乘法算法写出来，这道题咱们就几乎能解决了！

关于乘法算法，我觉得要关注以下三种情况：

1. 无需进行进位操作

   

   每一位数字乘上因数后均未超过9，无需进位。

2. 需要进行进位操作

   

   假设当前处理的是十位，十位数字乘上因数后为12，超过了9。将12“拆成”1和2，将最低位2保留下来，其余的数位1进入高位。

3. 需要进行进位操作，而且进了一位后的数位又可以再进一位

   

   假设当前处理的是百位，百位数字乘上因数后为49，超过了9。将49“拆成”4和9，将最低位9保留下来，其余的数位4进入高位。

   然而此时发现，之前在处理十位时，十位上的数字被拆分为1和4，其中1进入到百位，而百位现在的数字是9，9+1又可以向后进一位。

   9+1=10，因此将0保留下来，而1进入高位，加上之前进入高位的数字4，现在进入高位的数字是4+1=5。

   注：这是很容易被忽略的一种情况。

根据以上描述，可以发现在每次迭代中，我关注的是：

1. 当前处理的数位
2. 进入到下一位的数值

处理乘法中的进位#

上面给出的演示中，进入高位的数字都没有超过9，那么如果要进入高位的数字超过了9怎么办呢？

实际上这里和上面的处理方法是差不多的。

每次迭代中处理进到当前数位的数值时，将待进位的数值中的最低位进到当前的数位，在去除待进位的数值中的最低位后，剩余的数值留到后面处理更高位的进位。

咱做了一个动图来直观地演示一下这个过程：

代码实现乘法部分#

这里只截取了乘法部分，完整代码可以看下方题解代码

// arr是按数位储存结果的数组
// arrLen是上述数组的长度，也代表了结果数值的位数
// factor是每次迭代中要乘上的因数

// 将数组每一位都乘i，并进行进位处理(超过9的数字往高处进)
int j;
int carry = 0; // 要进到高位的数字
int multiplied; // 用于临时储存数组中每一位数字乘了因数之后的值
int calcDigit; // 用于临时储存新计算出来的某一个数位
for (j = 0; j < arrLen; j++) {
    multiplied = arr[j] * factor; // 每一位都乘i
    // multiplied % 10 取 <当前数位×因数> 的最低位，比如6*3=18>9，这个时候取出8，而1要进到高位
    // carry % 10 将 <上一次迭代留给本次迭代进位的数值> 的最低位取出，这一位是进到 <当前正在处理的数位> 的
    calcDigit = multiplied % 10 + carry % 10;
    // 运算留给 <下一次迭代> 进位的数值(carry)
    // 将 <进到当前数位的值> 去掉最低位(因为最低位在上面已经进到当前数位了)，加上multiplied要进到高位的数字
    carry = carry / 10 + multiplied / 10; 
    // 一种很容易错的情况，虽然multiplied % 10和carry % 10分别不会>=10，但是他们加起来是可能>=10的！
    // 也就是说，当前处理的数位在进位后可能>=10，需要再处理一道
    // 这种时候还要再进一次位
    if (calcDigit >= 10) {
        // 将除最低位外的数位加到 <下一次迭代> 进位的数值(carry)上
        carry += calcDigit / 10; 
        // 当前数位只保留最低位
        calcDigit %= 10;
    }
    // 存入最终运算出来的当前数位的值
    arr[j] = calcDigit;
    // j到数组边界了，但是还有要进到高位的数值，这说明位数不够了，那么就增加位数（增加数组元素）
    if (j >= arrLen - 1 && carry > 0) 
        arrLen++;
}

题解代码#

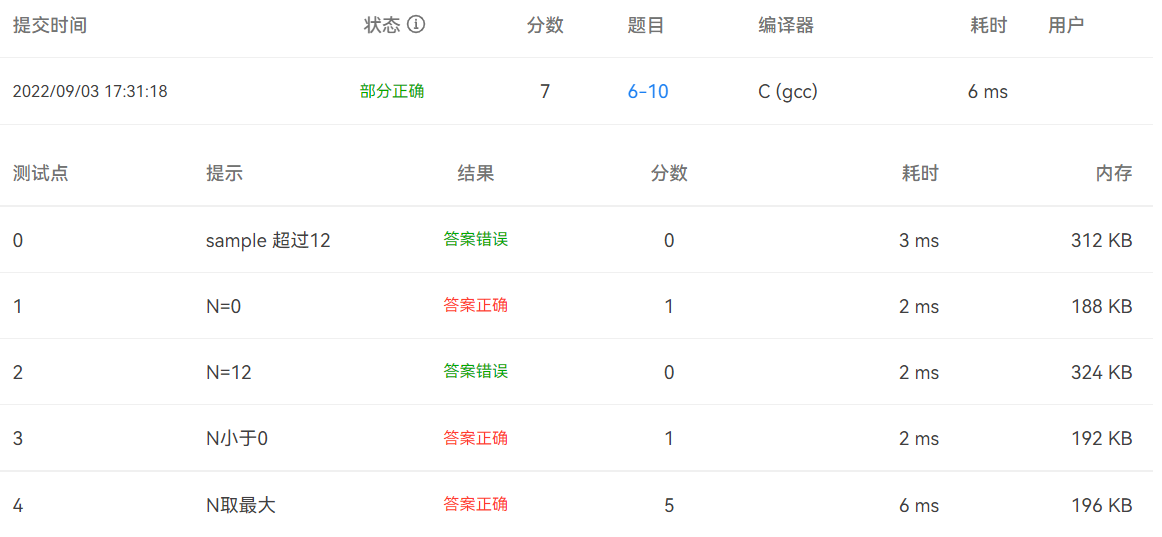
部分正确#

这部分正确的代码错就错在忽略了当前数位的二次进位问题。

展开查看详情

void Print_Factorial(const int N) {
    if (N < 0) {
        printf("Invalid input");
        return;
    }
    int arr[3000] = {}; 
    arr[0] = 1; 
    int arrLen = 1; 
    int factor = 2; 
    for (; factor <= N; factor++) {
        int j;
        int carry = 0; 
        int multiplied; 
        for (j = 0; j < arrLen; j++) {
            multiplied = arr[j] * factor; 
            arr[j] = multiplied % 10 + carry % 10;
            carry = carry / 10 + multiplied / 10; 
            // 这里少考虑了一种情况
            if (j >= arrLen - 1 && carry > 0) 
                arrLen++;
        }
    }
    int i;
    for (i = arrLen - 1; i >= 0; i--) {
        printf("%d", arr[i]);
    }
}

Accepted的代码#

void Print_Factorial(const int N) {
    if (N < 0 || N > 1000) {
        printf("Invalid input");
        return;
    }
    /*
        如果阶乘结果大到C语言中任意一种基本数据类型都无法表达，
        不妨考虑一下能不能用某种数据结构来解决问题
        这里采用数组
    */
    /* 1000个1000相乘：1*(10^(3*1000))=1e+3000,
        结果是1000000000....(3000个零)
        而本题N不超过1000，阶乘结果肯定也达不到1e+3000,
        这里就给数组分配3000个元素
    */
    // 从数组第一个元素为个位开始，往后数位升高
    int arr[3000] = {}; // 全初始化为0
    arr[0] = 1; // 个位为1
    int arrLen = 1; // 标记数组目前元素个数(结果位数)
    int factor = 2; // 从2开始乘，因为arr[0]=1
    for (; factor <= N; factor++) {
        int j;
        int carry = 0; 
        int multiplied; 
        int calcDigit; 
        for (j = 0; j < arrLen; j++) {
            multiplied = arr[j] * factor; 
            calcDigit = multiplied % 10 + carry % 10;
            carry = carry / 10 + multiplied / 10; 
            if (calcDigit >= 10) {
                carry += calcDigit / 10;
                calcDigit %= 10;
            }
            arr[j] = calcDigit;
            if (j >= arrLen - 1 && carry > 0) 
                arrLen++;
        }
    }
    // 打印结果数字
    int i;
    // 因为随着下标增加，数位升高，要打印出来正常的数值就得倒着遍历数组
    for (i = arrLen - 1; i >= 0; i--) {
        printf("%d", arr[i]);
    }
}

C++代码实现#

#include 
#include 

using namespace std;

int main()
{
    int n;
    cin >> n;                                   // 注意题目中说n为正整数，不用考虑0!的情况了
    vector<short> result{1};                    // 用一个vector容器按**从低位到高位**的顺序储存结果每一位数字
    int digitsNum = 1;                          // 储存位数，而不是老是用vector的size方法
    for (int factor = 2; factor <= n; factor++) // 从2开始乘
    {
        int carry = 0;     // 进位数
        int currDigit = 0; // 当前处理到的位数
        do
        {
            int mulDigit = 0;
            if (currDigit < digitsNum) // 不需要新增数位
            {
                mulDigit = result[currDigit] * factor; // 算出当前位乘上因子的结果
            }
            else
            { // 新增一位（在进位的时候会发生这种情况）
                result.push_back(0);
                digitsNum++;
            }
            int newDigit = mulDigit % 10 + carry % 10; // 将carry的最低位加上上面结果(mulDigit)的最低位，得到当前位的新值
            carry = carry / 10 + mulDigit / 10;        // 更新carry，除去最低位，并加上(multDigit)除最低位外的数
            if (newDigit > 9)
            {
                // 进位后，新的一位又>9了，需要再进到高位
                carry += newDigit / 10;
                newDigit = newDigit % 10;
            }
            result[currDigit] = (short)newDigit;       // 更新当前位
            currDigit++;                               // 处理下一位
        } while (currDigit < digitsNum || carry != 0); // 位数没处理完，或者还有进位，循环就要继续
    }
    for (int i = digitsNum - 1; i >= 0; i--)
    {
        cout << result[i];
    }
    return 0;
}

提交结果截图#

• WA

  

• AC