常用排序算法总结对比

常用排序算法总结对比

---

每博一文案

有许多人告诉我们，前方有美丽的风景，却没有一个人能代替我们走过
这茫茫的夜路。在这个光怪陆离的人间，没有谁可以将日子过得行云流水，
那些历经劫数，尝遍百味的人都明白一个道理：不期盼别人，踏实而务实
让自己的生活简单而真实，我们遇到的所有难题都是为了让我们变得更加强大。
风雨过后，终会迎来彩虹，当那时，万物终将明朗，一切皆如你意。
                                    ——————   一禅心灵庙语
1
2
3
4
5
6

---

---

各大排序的比较

---

相关术语解释：

• 稳定： 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，则为 稳定 ，如：如果 a 原本在序列中 b 的前面，而当 a = b ，排序后，a 仍然在 b 的前面，则表示稳定 ； 如果排序后，a 不在 b 的前面了，则表示 不稳定 。注意: 这里所谓的 前面：指的是，只需要在前面就可以了，不需要前面多少位。
• 不稳定: 如上述 稳定的描述，不满足稳定的定义。

---

排序的稳定性有什么有呢 ？？ ？

假设我们有这样一个场景：面试：10 个人笔试编程题，其中有两个人的分数都是 100 分 分别是 小华，小红的，但是，我们只能录用一个人。其中小华 比 小红 提前了 半个小时，先提交的答案。这时显而易见，我们是录用先提交的 小华了。而不稳定的排序算法，是无法保证提前交答案的小华，是排序在小红的前面的，因为数值都是 100，而 我们的稳定的排序算法是可以保证，提前交答案的小华一定是在小红的前面的。这里就体现了，排序算法中稳定性的价值所在。

---

• 内排序(In-place) : 在排序的整个过程中，待排序的所有记录和操作都在内存中完成的。不可在磁盘中操作
• 外排序(Out-place): 由于排序的数据量太大，主要存放在磁盘中，因此不能将全部数据放入到内存中，而是将一部分的数据从磁盘中读入到内存中，而整个排序过程需要通过磁盘和内存之间数据传输才能进行。该部分内容在 🔜🔜🔜 动静图结合详解: 归并排序 ，计数排序（归并排序思想扩展)那一块，会讲解的比较详细。大家可以移步，看看。
• 时间复杂度： 一个算法执行时所耗费的时间，一般主要是指：最坏情况下执行的所耗费的时间
• 空间复杂度: 运行完一个程序所需的内存大小，同样一般主要是指：最坏情况下的所耗费的空间
• n : 数据量（数据规模)
• k : 数据的个数
• In-place: 不占用额外内存，内排序
• Out-place: 占用额外的内存，外排序

---

详细说明各大排序的稳定

我个人不希望大家，是单单的记住死记硬背，而是可以理解其中的缘由，而排序的稳定性比较好讲解，有比较重要，所以多唠唠。

• 冒泡排序: 两两比较相邻记录的关键字，如果反序，则交换，直到没有反序的记录为止。更详细的内容大家可以移步到 ：🔜🔜🔜 动静图结合——冒泡排序_ChinaRainbowSea的博客-CSDN博客

冒泡排序是 稳定的 ，因为：我们两两比较时，我们可以通过修改算法，当数值相同时，不交换，这样，前面出现的相同的数值就不会出现在后面同样的是数值后面了。如下图所示:

---

• 选择排序： 通过查找 n-1 次数值间的比较，从 n -i+1 个数据中选出序列中最小的数值，并和 第 i ( 1<= i <= n)个数值交换。更详细的内容大家可以移步到 ：🔜🔜🔜 数据结构：静动图结合,活灵活现 讲解—— 堆排序, 直接选择排序_ChinaRainbowSea的博客-CSDN博客

选择排序是：不稳定的，可能存在，经过排序后，会改变相同数值的顺序。这时通过算法无法改变的。

---

• 插入排序: 将一个数值插入到已经排好序的有序表中，从而得到一个新的，记录新增 1 的有序表；更详细的内容大家可以移步到 ：🔜🔜🔜 图文并茂 —— 插入排序，希尔排序_ChinaRainbowSea的博客-CSDN博客

插入排序是 稳定的 ，我们可以通过算法，将相同的数值，不改变其顺序，如下图:

---

• 希尔排序： 将相距某个”gap 分组“的记录组成一个子序列，进行预排序，这样才能保证子序列内分别进行直接插入排序后，得到的结果基本游学而不是局部有序。更详细的内容大家可以移步到 ：🔜🔜🔜 图文并茂 —— 插入排序，希尔排序_ChinaRainbowSea的博客-CSDN博客

希尔排序是 不稳定 的，因为预排序会打乱相同数值原本的顺序，相同的数值可能会分到不同的组中，进行排序，该现象无法通过算法改变。如下图：

---

• 堆排序: 将待排序的序列构造成一个 大顶堆 ，此时，整个序列的最大值就是堆顶的根节点，将它移走（其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值），然后将剩余的 n-1 个序列重新构造一个堆，这样就会得到 n 个元素中的次大值。更详细的内容大家可以移步到 ：🔜🔜🔜 数据结构：静动图结合,活灵活现 讲解—— 堆排序, 直接选择排序_ChinaRainbowSea的博客-CSDN博客

堆排序是 不稳定 的，因为在堆排序中，升序，建大顶堆，后交换末尾元素 与 堆顶最大值，又重新建堆，这样的操作，改变了相同数值之间原来的前后顺序。如下图:

---

• 归并排序: 假设初始序列有 n 个记录，则可以看成是 n 个有序的子序列，每个子序列的长度为 1 ,然后两两归并，得到 [n/2] (x 表示不小于 x 的最小整数) 个长度为 2 或 1 的有序子序列；再两两归并，…,如此重复，直至得到一个长度为 n 的有序序列为止。更详细的内容大家可以移步到 ：🔜🔜🔜 动静图结合详解: 归并排序 ，计数排序_ChinaRainbowSea的博客-CSDN博客

归并排序是 稳定 的，可以通过算法到达，相同数值之间原来的顺序不发生改变。如下图所示:

---

• 快速排序: 通过一趟排序将待排序记录分割成独立的两部分，其中一部分记录的数值均比另一部分数值的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序的目的。更详细的内容大家可以移步到 ：🔜🔜🔜 “一万字”动静图生动结合详解:快速排序_ChinaRainbowSea的博客-CSDN博客

快速排序是 不稳定 的，取分界值，用于分界时，可能会改变相同数值之间原来的前后顺序。如下图:

---

• 计数排序: 通过统计序列中所有数值出现的个数，最后按照统计的个数一一映射到对应的下标位置上，实现排序，计数排序，并没有经过比较判断数值的大小的一种排序。更详细的内容大家可以移步到 ：🔜🔜🔜 动静图结合详解: 归并排序 ，计数排序_ChinaRainbowSea的博客-CSDN博客

计数排序是 稳定 的，通过依次统计序列出现的个数，原本顺序是如何就是，如何，相同的数值之间的顺序前后，不会发生改变。具体如下图：

---

• 基数排序: 依次分别取它们的 个位 ，十位 ，百位 ，千位 ，万位 … 排序好

具体如下：动图如下：

---

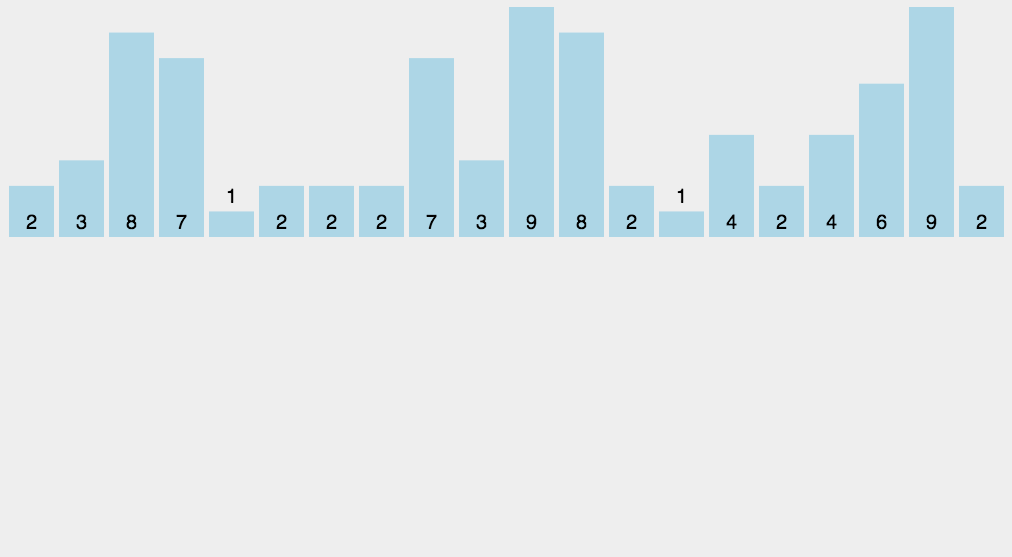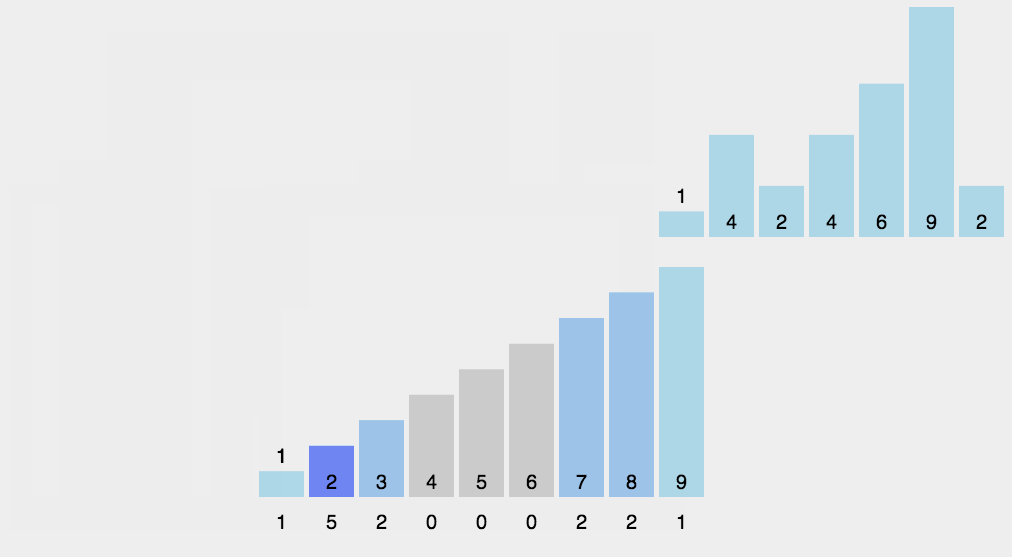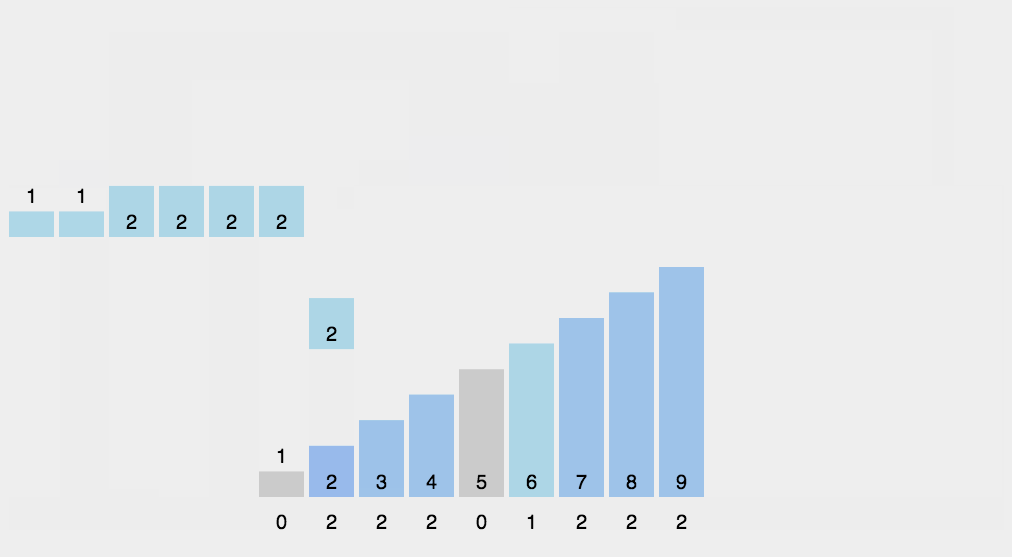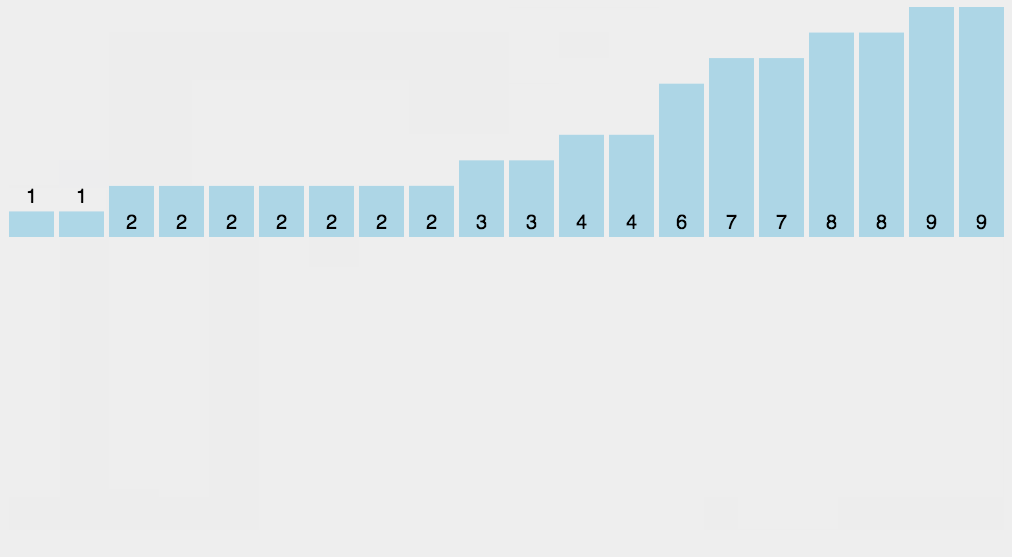
1. 我们需要一个无序的序列，如下图：

2. 比较序列中 个位 上的数值排序，

3. 再根据排序好的个位 上的顺序，进行 十位 上的数值排序，数位上较短的数 前面补零

4. 最后基于上述的十位 排序好的顺序，再进行 百位 上的数值排序，因为该序列最高数值直到了百位，所以我们只需要排序到 百位 就整体有序了。数位上较短的数 前面补零
   

---

• 基数排序是对 传统桶排序 的扩展，速度很快
• 是经典的空间换时间的方式，占用内存空间很大

当数据量太大的时候，所耗费的额外空间较大，是原始数据的 10 倍空间

• 基数排序是稳定的，相同的数，排序之后，他们的先后顺序没有发生变化。
• 基数排序，无法对负数以及小数进行排序。

---

最后:

限于自身水平，其中存在的错误，希望大家给予指教，韩信点兵——多多益善，谢谢大家，后会有期，江湖再见 !!!

---