第四章 神经网络的学习——数据&损失函数&数值微分&神经网络的梯度&学习算法的实现

1.数据

*机器学习中，一般将数据分为训练数据和测试数据两部分，首先使用训练数据进行学习，寻找最优的参数，然后使用测试数据评价训练的到的模型的实际能力。获得泛化能力是机器学习的最终目标

2.损失函数

*神经网络的学习通过某个指标表示现在的状态，然后以这个指标为基准，寻找最优权重参数，神经网络的学习中所用的指标称为损失函数，这个损失函数可以使用任意函数，但一般用均方误差和交叉熵误差等。

*损失函数是表示神经网络性能的“恶劣程度”的指标

*在神经网络的学习中，寻找最优参数（权重和偏置）时，要寻找使损失函数的值尽可能小的参数，因此需要计算参数的导数，然后以这个导数为指引，逐步更新参数的值

（1）均方误差

yk表示神经网络的输出， tk表示正确解， k表示数据的维度

 2）交叉熵误差

（3）mini-batch交叉熵误差

   计算损失函数时，必须将所有的训练数据作为对象

 

np.random.choice()可以从指定的数字中随机选择想要的数字，比如np.random.choice(60000,10)会从0到59999之间随机选择10个数字

3.数值微分

（1）导数

   表示某个瞬间的变化量

（2）偏导数

（3）梯度

   由全部变量的偏导数汇总而成的向量称为梯度，例如

 

梯度指示的方向是各点处的函数值减小最多的方向

   虽然梯度的方向并不一定指向最小值，但沿着它的方向能够最大限度地减小函数的值，因此，在寻找函数的最小值的位置时，要以梯度的信息为线索，决定前进的方向

（4）梯度法

函数的取值从当前位置沿着梯度的方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度的方向前进，如此反复，不断沿梯度方向前进

 用数学式表示梯度法：

η表示更新量，在神经网络的学习中称为学习率，学习率决定再一次学习中，应该学习多少，以及在多大程度上更新参数，学习率需要实现确定为某个值，比如0.01或0.001，一般而言，这个值过大或过小都无法“到达最优位置”。

 

像学习率这样的参数称为超参数，一般来说，超参数需要尝试多个值，以便找到一种可以使学习顺利进行的设定

4.神经网络的梯度

*是指损失函数关于权重参数的梯度，例如有一个形状为2*3的权重W的神经网络，L表示损失函数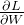， 表示梯度：

元素 表示当w11 稍微变化时，损失函数L会发生多大变化

*求梯度的代码如下：

 *使用求梯度的类：

5.学习算法的实现

*神经网络的学习步骤：

   （1）前提：神经网络存在合适的权重和偏置，调整权重和偏置以便拟合训练数据的过程称为学习

   （2）步骤一（mini-batch）：从训练数据中随机选出一部分数据，这部分数据称为mini-batch，目标是减小mini-batch损失函数的值

   （3）步骤二（计算梯度）：为了减小mini-batch的损失函数的值，需要求出各个权重参数的梯度，梯度表示损失函数的值减小最多的方向

   （4）步骤三（更新参数）：将权重参数沿梯度方向进行微小更新

   （5）步骤四（重复）：重复步骤一、步骤二、步骤三

*以2层神经网络为对象，使用MNIST数据集进行学习

   将这个2层神经网络实现为一个名为TowLayerNet的类

\ch04\two_layer_net.py

   使用MNIST进行学习

\ch04\train_neuralnet.py

链接：https://pan.baidu.com/s/15DiwneQN-pI73il5pif-vA?pwd=1212 
提取码：1212