• 2022_08_13__106期__排序

    目录

    希尔排序：

    直接选择排序：

    冒泡排序：

    快速排序：

    希尔排序：

    希尔排序本质上是插入排序的升级。

    希尔排序的第一个步骤是预排序：预排序的目的是大体的把数组的元素的左边分成较小的数，数组的元素的右边分成较大的数。

    我们用图像进行演示：

    预排序：间隔为gap的数据分为一组，插入排序。

     假如我们的gap为3

     我们可以把这部分元素分成三组。

     我们对间隔为gap的元素进行插入排序

     对应的新数组为

     可以发现，右侧的数据是偏大的。

    我们先写一个单趟排序：

    1. void ShellSort(int *a, int n)
    2. {
    3. 	int gap;
    4. 	int end;
    5. 	int tmp = a[end + gap];
    6. 	while (end >= 0)
    7. 	{
    8. 		if (a[end] > tmp)
    9. 		{
    10. 			a[end + gap] = a[end];
    11. 			end -= gap;
    12. 		}
    13. 		else
    14. 		{
    15. 			break;
    16. 		}
    17. 	}
    18. 	a[end + gap] = tmp;
    19. }

    我们对代码进行分析：

    gap表示我们的间距，end表示我们末尾的数据，tmp表示与末尾数据相隔gap的下一个数据，也就是我们要插入的数据。

    我们调用while循环，当end>=0，进入循环。我们要把数据排列成从小到大的顺序，当前一位的数据大于新插入的数据，我们把原数据放到其下一位，然后end-=gap。当前面所有的数据都大于新插入的数据时，这时候，end=-3，我们需要把新数据插入到数组头部，也就是a[0]的位置

    当前一位的数据始终小于新插入的数据，就满足我们的从小到大的顺序，我们就把新的数据放到数组的末尾。

    下面表示我们对组进行排序：

    1. void ShellSort(int*a, int n)
    2. {
    3. 	int gap;
    4. 	for (int i = 0; i<n; i += gap)
    5. 	{
    6. 		int end = i;
    7. 		int tmp = a[end + gap];
    8. 		while (end >= 0)
    9. 		{
    10. 			if (a[end] > tmp)
    11. 			{
    12. 				a[end + gap] = a[end];
    13. 				end -= gap;
    14. 			}
    15. 			else
    16. 			{
    17. 				break;
    18. 			}
    19. 		}
    20. 		a[end + gap] = tmp;
    21. 	}
    22. }

    我们创建一个for循环，用变量i来限制end的大小。

    但是这里的for循环的限制条件写错了，i

    所以我们要把这里的i 

    1. void ShellSort(int*a, int n)
    2. {
    3. 	int gap;
    4. 	for (int i = 0; i<n-gap; i += gap)
    5. 	{
    6. 		int end = i;
    7. 		int tmp = a[end + gap];
    8. 		while (end >= 0)
    9. 		{
    10. 			if (a[end] > tmp)
    11. 			{
    12. 				a[end + gap] = a[end];
    13. 				end -= gap;
    14. 			}
    15. 			else
    16. 			{
    17. 				break;
    18. 			}
    19. 		}
    20. 		a[end + gap] = tmp;
    21. 	}
    22. }

    上面的只是表示我们只排序了一组数据，还有两组数据需要排序。

    1. void ShellSort(int*a, int n)
    2. {
    3. 	int gap = 3;
    4. 	for (int j = 0; j < gap; ++j)
    5. 	{
    6. 		for (int i = j; i < n - gap; i += gap)
    7. 		{
    8. 			int end = i;
    9. 			int tmp = a[end + gap];
    10. 			while (end >= 0)
    11. 			{
    12. 				if (a[end]>tmp)
    13. 				{
    14. 					a[end + tmp] = a[end];
    15. 					end -= gap;
    16. 				}
    17. 				else
    18. 				{
    19. 					break;
    20. 				}
    21. 			}
    22. 			a[end + gap] = tmp;
    23. 		}
    24. 	}
    25. }

    我们再使用一次for循环，因为我们的排序的组数最多只有gap组，所以我们让j小于gap

    我们让j来限制i从而达到排序三组。

    我们可以对代码进行简化：

    1. void ShellSort(int*a, int n)
    2. {
    3. 	int gap = 3;
    4. 		for (int i = 0; i < n - gap; i ++)
    5. 		{
    6. 			int end = i;
    7. 			int tmp = a[end + gap];
    8. 			while (end >= 0)
    9. 			{
    10. 				if (a[end]>tmp)
    11. 				{
    12. 					a[end + tmp] = a[end];
    13. 					end -= gap;
    14. 				}
    15. 				else
    16. 				{
    17. 					break;
    18. 				}
    19. 			}
    20. 			a[end + gap] = tmp;
    21. 		}
    22. }

     前面的写法是一组一组的处理，这里的方法是一个一个的处理。

    gap越大，大的数据越快跳到后面。

    小的数据越快跳到前面

    gap越小，大的数据越慢跳到后面

    小的数据越满跳到前面

    gap越小，数组的元素越接近有序。

    实现希尔排序：

    1. void ShellSort(int*a, int n)
    2. {
    3. 	int gap = n;
    4. 	while (gap > 1)
    5. 	{
    6. 		gap = gap / 3 + 1;
    7. 		for (int i = 0; i < n - gap; i++)
    8. 		{
    9. 			int end = i;
    10. 			int tmp = a[end + gap];
    11. 			while (end >= 0)
    12. 			{
    13. 				if (a[end]>tmp)
    14. 				{
    15. 					a[end + gap] = a[end];
    16. 					end -= gap;
    17. 				}
    18. 				else
    19. 				{
    20. 					break;
    21. 				}
    22. 			}
    23. 			a[end + gap] = tmp;
    24. 		}
    25. 	}
    26. }
    1. int gap = n;
    2. 	while (gap > 1)
    3. 	{
    4. 		gap = gap / 3 + 1;

    当gap>1时，始终是预排序，当gap=1时，是插入排序。

    gap=gap/3+1能够保证gap最终的结果肯定为1。

    总结：希尔排序我们可以这样理解：我们通过初始值较大的gap逐步的把数组元素变成有序，最终的gap为1，相当于我们直接使用插入排序，因为前面的预处理，导致这时候的数组已经接近有序，所以我们的插入排序的时间复杂度就会很小，从而达到缩短运行时间的目的。

    希尔排序的时间复杂度大概为O(N^1.3).

    直接选择排序：

    直接选择排序的过程是在一个数组中首先把最小的数据找出来，放在第一位，再找最小的，放在第二位，再找最小的，放在第三位。

    所以这种算法的时间复杂度为O(N^2)

    1. void SelectSort(int*a, int n)
    2. {
    3. 	int begin = 0, end = n - 1;
    4. 	while (begin < end)
    5. 	{
    6. 		int mini = begin, maxi = begin;
    7. 		for (int i = begin + 1; i <= end; ++i)
    8. 		{
    9. 			if (a[i]>a[maxi])
    10. 			{
    11. 				maxi = i;
    12. 			}
    13. 			if (a[i] < a[mini])
    14. 			{
    15. 				mini = i;
    16. 			}
    17. 		}
    18. 		Swap(&a[begin], &a[mini]);
    19. 		if (maxi == begin)
    20. 		{
    21. 			maxi = mini;
    22. 		}
    23. 		Swap(&a[end], &a[maxi]);
    24. 		++begin;
    25. 		--end;
    26. 	}
    27. }

    我们的思路是这样的：首先，我们遍历整个数组，找到最小的元素和最大的元素，把最小的元素放在数组头，把最大的元素放到数组尾，再进行遍历其余的元素，把最小的元素放到第二位，把最大的元素放到倒数第二位等等。

    我们对代码进行分析：

    int begin = 0, end = n - 1;

    begin和end分别代表数组头和数组尾的下标。

    int mini = begin, maxi = begin;

    这里表示我们从头开始遍历。

    1. for (int i = begin + 1; i <= end; ++i)
    2. 		{
    3. 			if (a[i]>a[maxi])
    4. 			{
    5. 				maxi = i;
    6. 			}
    7. 			if (a[i] < a[mini])
    8. 			{
    9. 				mini = i;
    10. 			}
    11. 		}

    这里表示我们从数组的第一位开始到最后一位，让他们与a【maix】进行比较，把其中较大的小标赋给maxi，把其中较小的下标赋给mini。这里我们就找到了最大的数据和最小的数据对应的下标，然后根据下标把最大的数据放在后面，把最小的数据放在前面，但是注意：当我们的起始位置对应的元素为最大的元素时，我们把最小的数据和起始位置进行交换，那么起始位置对应的数据就变成了最小的数据，我们再进行交换时就会发生错误，所以我们这里要进行判断：加入maxi和begin相等时，因为我们把最小的值和起始位置的值已经完成了交换，所以我们最小值对应的下标就是最大值对应的下标，所以我们把最小值对应的下标赋给最大值对应的下标。

    直接选择排序的时间复杂度为O(N)

    冒泡排序：

    单躺排序：

    1. void BubbleSort(int*a, int n)
    2. {
    3. 	for (int i = 0; i < n-1 ; ++i)
    4. 	{
    5. 		if (a[i]>a[i+1])
    6. 		{
    7. 			Swap(&a[i], &a[i+1]);
    8. 		}
    9. 	}
    10. }

    我们画图进行解释：

     加入对于这样的一个数组，我们要进行冒泡排序：我们的数组的元素个数为6，n=6

    经过遍历，得到的结果为

     我们只是把最大的数字移到了左侧，接下来，我们要找出前五个数字的最大数据，我们继续套用循环。

    1. void BubbleSort(int*a, int n)
    2. {
    3. 	for (int j = 0; j < n-1, ++j)
    4. 	{
    5. 		for (int i = 0; i < n-1-j; ++i)
    6. 		{
    7. 			if (a[i ]>a[i+1])
    8. 			{
    9. 				Swap(&a[i], &a[i+1]);
    10. 			}
    11. 		}
    12. 	}
    13. }

    这个是没有经过优化的冒泡排序。

    优化的冒泡排序：

    1. void BubbleSort(int*a, int n)
    2. {
    3. 	for (int j = 0; j < n - 1, ++j)
    4. 	{
    5. 		int exchange = 0;
    6. 		for (int i = 0; i < n - 1 - j; ++i)
    7. 		{
    8. 			if (a[i]>a[i + 1])
    9. 			{
    10. 				Swap(&a[i], &a[i + 1]);
    11. 				exchange = 1;
    12. 			}
    13. 		}
    14. 		if (exchange == 0)
    15. 		{
    16. 			break;
    17. 		}
    18. 	}
    19. }

    第一层循环中，我们置exchange为0，当两数有完成交换的时候，我们把exchange置为1，之后，加入exchange为0的时候，表示我们数组中的元素已经是有序的了，那我们就退出函数。

    冒泡排序的时间复杂度最坏情况下为O(N^2)

    冒泡排序的时间复杂度最好情况下O(N).

    快速排序：

     如图像所示：我们可以先确定key，key可以是数组头的数据，也可以是数组尾的数据。

    当key为数组头为6时，我们先让R走，右侧的R找的是比key更小的值，左测的L找的是比KEY更大的值

     这时候，让L和R对应的值进行交换

     R继续找小，L找大

     再进行交换。

     R继续找小

     然后L找大，L和R相遇，相遇到3，我们把相遇的节点对应的值和key进行交换。

     所以数组对应的数据为3 1 2 5 4 6 9 7 10 8

    我们单次排序的结果就是找到key对应的下标

    对应的代码：

    1. void PartSort(int*a, int left, int right)
    2. {
    3. 	int keyi = int left;
    4. 	while (left < right)
    5. 	{
    6. 		while (a[right] >= a[keyi])
    7. 		{
    8. 			--right;
    9. 		}
    10. 		while (a[left] <= a[keyi])
    11. 		{
    12. 			++left;
    13. 		}
    14.         if (left<right)
    15. 		Swap(&a[left], &a[right]);
    16. 	}
    17. 	Swap(&a[left], &a[keyi]);
    18. }
    19.

    我们对代码进行分析：

    我们首先把keyi设置为数组头元素。

    当left小于right的时候，我们开始进行遍历：我们在右侧找小，当右侧对应的元素大于keyi对应的元素的时候，我们继续让right--，当右侧元素小于或等于keyi对应的元素时，我们停止。

    注意：这里也要包括等于，如图所示：

    我们进行遍历：

     这时候，L和R停止，我们发生交换，交换后L和R还会停止，我们再发生交换，一直持续下去就会导致死循环的问题。

    但是这里的判断条件还是有问题的：可能会导致错过的情况。

     R先走，找小。

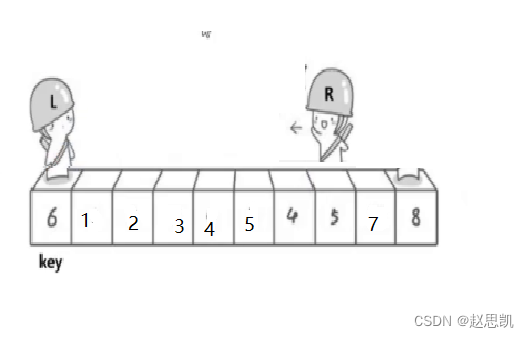
    然后L找大，

     

     

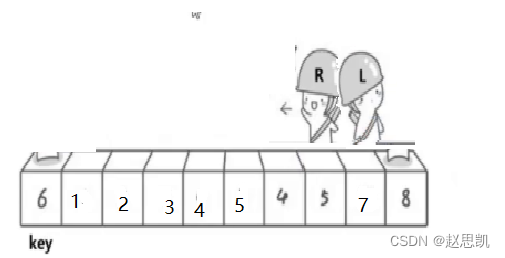
    这时候就会产生错过的情况，所以我们要这样写代码：

    1. void PartSort(int*a, int left, int right)
    2. {
    3. 	int keyi = int left;
    4. 	while (left < right)
    5. 	{
    6. 		while (left < right&&a[right] >= a[keyi])
    7. 		{
    8. 			--right;
    9. 		}
    10. 		while (left < right&&a[left] <= a[keyi])
    11. 		{
    12. 			++left;
    13. 		}
    14. 		if (left<right)
    15. 		Swap(&a[left], &a[right]);
    16. 	}
    17. 	Swap(&a[left], &a[keyi]);
    18. }

    当既找到小，又找到大的时候，并且左小于右的时候，我们把小和大的进行交换。

    当left=right时，表示左右指针已经重合，这时候，我们把keyi和left下标对应的元素进行交换完成了。

    这时候，对应的元素被我们分成两段：

     分别是3 1 2 5 4和9 7 10 8

    然后我们再次对他们两个进行单趟排序，我们首先对前面的5个进行排序：

     最后实现的结果是：

     又分割成两个，我们再对前一个进行排序：

    1比2小，然后L走

     然后我们实现交换。

     我们再进行分割：

    我们分割的区间是[begin,keyi-1] keyi[keyi+1,right]

    begin为0，keyi-1的结果为0，keyi+1的结果为[2,1]，不符合条件，所以不能再分割。

    1. int PartSort(int*a, int left, int right)
    2. {
    3. 	int keyi = a[left];
    4. 	while (left < right)
    5. 	{
    6. 		while (left < right&&a[right] >= a[keyi])
    7. 		{
    8. 			right--;
    9. 		}
    10. 		while (left < right&&a[left] <= a[keyi])
    11. 		{
    12. 			left++;
    13. 		}
    14. 		if (left < right)
    15. 		{
    16. 			Swap(&a[left], &a[right]);
    17. 		}
    18. 	}
    19. 	int meeti = left;
    20. 	Swap(&a[metti], &a[keyi]);
    21. 	return meeti;
    22. }

  • 相关阅读:
    [2022-11-28]神经网络与深度学习 hw10 - LSTM和GRU
    vue中wtach和computed的区别与联系
    操作系统：进程退出，进程等待，进程替换，简单的shell命令行解释器
    【ES6】
    我用ChatGPT做WebRTC音视频性能优化，主打一个高效
    使用Android原生制作毛玻璃效果图片
    JavaScript之正则表达式的使用方法详细介绍
    【JavaEE】_Spring MVC项目之使用对象传参
    数据结构篇：链表和树结构的操作方法
    线性代数的本质(十一)——复数矩阵
  • 原文地址：https://blog.csdn.net/qq_66581313/article/details/126658486