-
神经网络(十二)卷积神经网络DLC
卷积神经网络的本质是将全连接神经网络的全连接层替换为卷积层,所以下面我们从全连接神经网络开始。
一、全连接神经网络
1.神经元
单个神经元由输入;权重;激活函数;输出组成
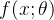
其中涉及计算的部件为:权重&激活函数
①权重

结合图例可以得,z为所有输入量的加权和,算式中的w为权重向量,b为偏置
②激活函数
名称 原型函数 变体 变体函数 Logistic函数 
Hard-Logistic函数 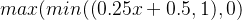
Tanh函数 
Hard-Tanh函数 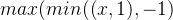
ReLU函数 
带泄露的ReLU 
带参数的ReLU 
ELU函数 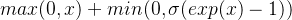
Softplus函数 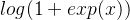
Swish函数 
GELU函数 
Tanh近似 
Logistic近似 
MaxOut单元 ![\underset{k\in [1,K]}{max}(z_k)](https://1000bd.com/contentImg/2023/10/30/232845674.png)
详细原型以及性质参见 激活函数DLC
2.网络结构
前馈神经网络由输入层、隐藏层、输出层组成

其信息通过不断迭代下列公式进行传递,以第
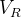 层为例
层为例净输入(净活性值):
 权重×上一层的输出+偏置
权重×上一层的输出+偏置输出(活性值):
 对净输入取激活函数
对净输入取激活函数可以合并为:
 或
或 
将整个网络视为复合函数
 ,可得信号的传播如下
,可得信号的传播如下
!!!通用近似定理:常见的连续非线性函数均可以前馈神经网络拟合(万能公式)
可以将输出以如下形式表示

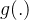 为分类器,即最后一层的激活函数
为分类器,即最后一层的激活函数3.参数学习
前馈神经网络的参数迭代方向与数据流动方向相反,其因此得名。
对样本(x,y)采用交叉熵损失函数

!交叉熵损失函数:
 p为正确答案,q为预测值
p为正确答案,q为预测值对给定的训练集D=(
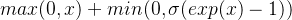 ),其结构化风险函数为:
),其结构化风险函数为:
其中
 为模型的复杂度,
为模型的复杂度,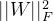 一般为正则化项,使用Frobenius范式
一般为正则化项,使用Frobenius范式 仅含权重
仅含权重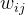 ,不含偏置b
,不含偏置b通过计算
 和
和 来获得需更新的参数,可以通过链式法则/反向传播算法来计算,但是一般用反向传播算法(链式法则算到死)
来获得需更新的参数,可以通过链式法则/反向传播算法来计算,但是一般用反向传播算法(链式法则算到死)链式法则:就是分步求导
4.梯度计算
对第
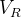 层而言
层而言权重
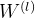 的梯度为:
的梯度为:
偏置
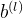 的梯度为:
的梯度为: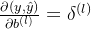
①反向传播计算
大致分为如下3步
step1.前馈计算每一层的净输入
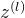 和激活值
和激活值 ,直至最后一层
,直至最后一层step2.反向传播计算每层的误差

step3.计算每一层参数的偏导,并更新相关参数

②自动梯度计算
以代码实现链式法则的迭代梯度计算(可以优先使用)
有以下实现方式:
Cat1.数值微分(导数定义)

Cat2.符号微分
Cat3.自动微分
令复合函数
 ,得出计算图;再将每一步对应的函数的和导数记录,需要计算时候,由链式法则连乘即可。如下
,得出计算图;再将每一步对应的函数的和导数记录,需要计算时候,由链式法则连乘即可。如下

自动微分有以下模式:
1.前向模式:计算方向与信息传播的方向一致(前进时求导)
2.反向模式:等同于反向传播算法
3.静态图模式:编译时构建,程序运行时不再改变
优点:构建时可以进行优化,并行能力强
缺点:灵活性较差
4.动态图模式:程序运行时动态构建
优点:灵活性高
缺点:不易优化,难以并行计算

5.优化问题
①非突优化问题
②梯度消失问题
经过逐层递减,会使得网络越来越难以训练。简单的方法是使用导数较大的激活函数,如ReLU
更多细节详见神经网络(七)优化与正则化
二、卷积神经网络
CNN,是一种具备局部连接、权重共享的深层前馈神经网络。
解决了全连接神经网络的两个问题:
①参数太多:难以训练,且易过拟合
②局部特征不变:难以提取缩放、平移、旋转等不改变语义的信息
CNN具备三个特性:①局部连接 ②权重共享 ③汇聚
1.卷积
当前时刻产生的信息与之前时刻的延迟信息的叠加
一维卷积:

二维卷积:

变种卷积:
名称 特征 空洞卷积 作用:增加输出单元的感受野
在卷积核中插入空洞,变相的增加卷积核的大小(投射的时候增加空位)
转置/微步卷积 低维特征映射到高维特征(放大)
减小步长,在输入上插入空洞(S=1/2)
详见 卷积运算DLC
2.卷积层和汇聚层
使用卷积层替代全连接层:
 ->
-> 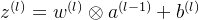


卷积层具备两个重要特征:
局部连接:减少连接数量,由
 变为
变为 (K为卷积核大小)
(K为卷积核大小)权重共享:可理解为卷积核仅捕捉输入数据中的一种特定局部特征(若要捕获多个则需要多个卷积核),由于这种性质,卷积层仅有 K维权重
 和一维偏置
和一维偏置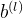 ,与参与运算的神经元数量无关。
,与参与运算的神经元数量无关。①卷积层
一般卷积层由以下部件组成:输入特征映射组 + 输出特征映射组 + 卷积核

使用卷积核
 ...
... 分别对输入特征映射
分别对输入特征映射 ...
... 进行卷积,再加上偏置b得到净输入
进行卷积,再加上偏置b得到净输入 ,再过激活函数后得到输出特征映射
,再过激活函数后得到输出特征映射
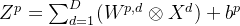

虽然卷积的连接方式为单连接,但输入和输出之间可以等效为全连接。
计算过程如图所示

②汇聚层
又称子采样层,用于进行特征选择,降低特征数量,从而减少超参数数量。常见的汇聚有以下几种:(对于区域
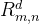 )
)1.最大汇聚:
 (选取区域内活性的最大值)
(选取区域内活性的最大值)
2.平均汇聚:
 (选取区域内活性平均值)
(选取区域内活性平均值)主流神经网络中,汇聚层仅包含下采样操作;但早期神经网络中,还包含了非线性激活函数。
3.整体结构
一个经典CNN由卷积层、汇聚层、全连接层交叠而成,卷积层包含了卷积和激活函数

最后需要全连接层进行分类
现代卷积网络倾向于使用较小的卷积核(如3x3和1x1)并增加深度,且汇聚层的比例逐渐降低。
4.参数学习
CNN结构上类似于前馈神经网络,亦可通过反向传播算法来进行参数学习。仅需计算卷积核中参数的梯度即可
其损失函数
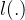 关于第
关于第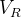 层可得偏导
层可得偏导
![\frac{\partial l}{\partial b^{(l,p)}}=\sum_{i,j}[\delta^{(l,p)}]_{i,j}](https://1000bd.com/contentImg/2023/10/30/232845033.png)
反向传播算法(第
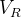 层的第p个特征映射的误差项
层的第p个特征映射的误差项 为)
为)汇聚层:
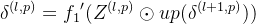
卷积层:

5.几种经典CNN
①LeNet-5

②AlexNet

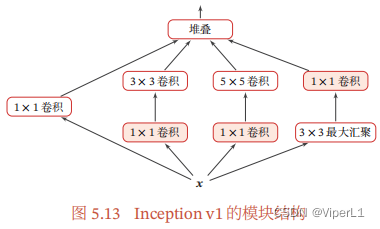
③Inception网络
由大量Inception v1模块堆叠而成
④残差网络
残差单元通过为非线性的卷积层增加直连边的方式提高信息传播效率,残差网络是将大量残差单元串联而成
目标函数h(x)由两部分组成:恒等函数
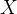 和残差函数
和残差函数 

以非线性单元
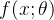 逼近残差函数
逼近残差函数  ,可得
,可得
典型残差单元结构

三、卷积神经网络的图解以及应用
1.图解CNN的运行
一般的卷积模块由:卷积、汇聚、激活组成,通过叠加可以构成卷积神经网络。
①卷积
卷积核一般以矩阵的形式表达,用以捕获某种特征;
例如下面三个矩阵分别可以识别左斜线、交叉和右斜线
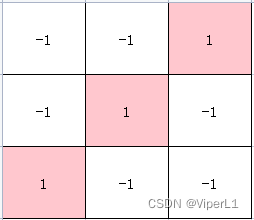

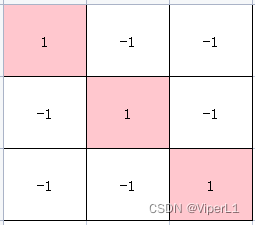
通过卷积核与原图(一般会切分为小块)的计算(可以视为于相似度)

 的结果为3,再通过另一个矩阵存储这个结果
的结果为3,再通过另一个矩阵存储这个结果
②汇聚/池化
使用极大汇聚/平均汇聚均可,用于压缩矩阵,提高计算效率的同时可以避免过拟合,从而提高网络的泛化能力
 如图矩阵最终结果为9
如图矩阵最终结果为9③激活
一般使用ReLU(max(x,0))激活函数,以避免梯度消失的问题
2.残差网络的Python实现

①引入数据包(Tensorflow)
- import tensorflow as tf
- from tensorflow import keras
- from tensorflow.keras import layers,Sequential
②实现残差单元
- class BasicBlock(layers.Layer): --继承自layers.Layer
- --初始化
- def__init__(self,filter_num,strides=1): --自指针,通道数,步长
- super(BasicBlock,self).__init__()
- self.conv1=layers.Conv2D(filter_num,(3,3),strides=strides,padding='same')--卷积层
- --通道数,卷积核尺寸,步长,补0
- self.bn1=layers.BatchNormalization() --偏置
- self.relu=layers.Activation('relu') --激活函数
- self.con2=layers.Conv2D(filter_num,(3,3),strides=1,padding='same')--不再进行下采样
- self.bn2=layers.BatchNormalization()
- if stride !=1 : --当步长不为1时,需要对短接边进行转换
- self.downsample=Sequential() --初始化短接边的容器
- self.downsample.add(layer.conv2D(filter_num,(1,1),strides))
- --在容器中添加一个1x1的矩阵,用于匹配段阶边与净输出
- else:
- self.downsample=lambda x:x
- --前向传播
- def call(self,inputs,training=None):
- out=self.conv1(inputs)
- out=self.bn1(out)
- out=self.relu(out) --激活函数
- out=self.conv2(out)
- out=self.bn2(out)
- identity=self.downsample(inputs) --短接边
- output=layers.add([out,identity]) --将短接边的举证与净输出矩阵求和
- output=tf.nn.relu(output) --激活函数
- return output
③实现残差网络
- class ResNet(keras.Model): --继承自keras.Model
- --构建残差网络
- def__init__(self,layer_dims,num_classes=100): #[2,2,2,2] --残差单元的,全连接层种类
- super(ResNet,self).__init__()
- self.stem=Sequential([layers.Conv2D(64,(3,3),strides=(1,1)), --初始化预处理层
- layers.BatchNormalization(),
- layers.Activation('relu'),
- layers.MaxPool2D(pool_size=(2,2),strides=(1,1),padding='same')])
- --布置残差网络内部,一般而言通道数量按块倍增
- self.layer1=self.build_resblock(64,layers_dims[0])
- self.layer2=self.build_resblock(128,layers_dims[1],strides=2)--后续的三组都可以降维
- self.layer3=self.build_resblock(256,layers_dims[2],strides=2)
- self.layer4=self.build_resblock(512,layers_dims[3],strides=2)
- #output:[b,512,h,w],
- self.avgpool=layers.GlobalAveragePooling2D()--自适应限缩
- self.fc=layers.Dense(num_classes) --用于分类的全连接层
- --实现前向传递
- def call(self,inputs,training=None):
- x=self.stem(iputs) --预处理层
- x=self.layer1(inputs) --残差网络计算
- x=self.layer2(inputs)
- x=self.layer3(inputs)
- x=self.layer4(inputs)
- x=self.avgpool(x) --全连接层分类
- x=self.fc(x)
- return x
- --构建残差模块(由多个残差单元堆叠而成,仅第一个残差单元允许下采样)
- def build_resblock(self,filter_num,blocks,strides=1):--通道数,层数,步长
- res_blocks=Sequential()
- res_blocks.add(BasicBlock(filter_num,strides)) --添加一个残差模块
- for_ in range(1,blocks):
- res_blocks.add(BasicBlock(filter_num,strides=1)) --后续残差模块不允许下采样
- return res_blocks
- def resnet18(): --18层的残差网络配置
- return ResNet([2,2,2,2])
- def resnet34(): --34层的残差网络配置
- return ResNet([3,4,6,3])
④应用
- model=resnet18() --获取18层的参数
- model.build(input_shape=(Node,32,32,3))
- optimizer=optimizers.Adam(lr=le-3)
- --训练
- for epoch in range(50):
- for step,(x,y) in enumerate(train_db):
- with tf.GradientTape() as tape:
- logits=model(x)
- y_onehot=tf.one_hot(y,depth=100)
- loss=tf.losses.ccatrgorical_crossentropy(y_onehot,logits,from_logits=True)
- loss=tf.reduce_mean(loss)
- grads=tape.gradient(loss,model.trainble_variables) --梯度
- optimizer.apply_gradients(zip(grads,model.trainable_variables))
- --测试
- total_num=0
- total_correct=0
- for x,y in test_db
- logits=model(x)
- prob=tf.nn.softmax(logits,axis=i)
- pred=tf.argmax(prob,axis=1)
- pred=tf.cast(pred,dtype=tf.int32)
- correct=tf.cast(tf.equal(pred,y),dtype=tf.int32)
- correct=tf.reduce_sum(correct)
- total_num+=x.shape[0]
- total_correct+=int(correct)
- acc=total_correct / total_num
- print(epoch,'acc:',acc)
-
相关阅读:
Fanuc发那科数采
Effective Modern C++[实践]->优先使用nullptr,而非0或NULL
git push出现git@github.com: Permission denied (publickey) 解决办法
Matlab:指定时区
YOLOv5、v7改进之二十七:解决小目标问题——校正卷积取代特征提取网络中的常规卷积
【OpenCV】- 图像修复
Linux系统编程(五):信号
Linux——进程池
VueUI Day05(8.4)Mint UI
uboot启动流程源码分析(一)
- 原文地址:https://blog.csdn.net/weixin_37878740/article/details/126655172
