• 神经网络（十一）卷积运算DLC

    卷积，主要用于信号的延迟累积，其输出结果是当前时刻产生的信息与之前时刻的延迟信息的叠加

            如：y_t=1 \times x_t+\frac{1}{2}\times x_{t-1}+\frac{1}{4}\times x_{t-2}

    一、一维卷积

            y_t=\sum_{k=1}^Kw_kx_{t-k+1}

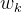            实质是w_k滤波器（或称卷积核）与信号的卷积； t为时刻，K为滤波器长度(总长)

                    实质上，单次的卷积运算可以定义为：y=w*x

                            *为卷积计算，数学上使用傅立叶变化，神经网络中一般转换为矩阵相乘

                    滤波器一般表达为w=[k_1,k_2,...k_n]，卷积相当于信号进行加权平移

                    ①例如滤波器为w=[1,-2,1] 时，实现对信号序列的二阶微分为

                             {x}''(t)=x(t+1)+x(x-1)-2x(t)

                    ②又如滤波器为w=[\frac{1}{3},\frac{1}{3},\frac{1}{3}] 能检测低频信号，w=[1,-2,1] 能检测高频信号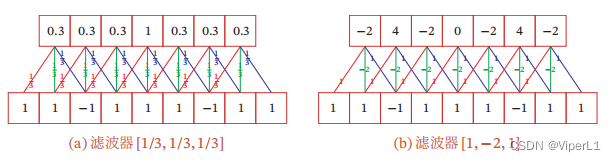

    二、二维卷积

            y_{ij}=\sum_{u=1}^U\sum_{v=1}^V w_{uv}x_{i-u+1,j-v+1}

            可以将净输入视为图像上的一个点(坐标为 i , j )，与滤波器 w 进行卷积Y=W*X

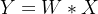
            图例如下：

            一般在处理图像的时候使用均值滤波，既当前图片的像素平均，w_{uv}=\frac{1}{UV}

            图像进过卷积操作的结果被称为特征映射

    三、互相关

            通过互相关操作来代替卷积核翻转，以减少不必要的运算开销。一般通过滑动窗口的点积来实现。

            对于给定的图像X和卷积核W，其互相关为

                    y_{ij}=\sum_{u=1}^U\sum_{v=1}^Vw_{uv}x_{i+u-1,j+v-1}        等价于        Y=W\otimes X=rot180(W)*X

                            其中rot180代表旋转180°

            1.卷积变种

                    通过引入滑动步长和零填充来增加卷积的多样性

                            滑动步长：卷积核滑动时的间隔

                            零填充：在向量两端补0

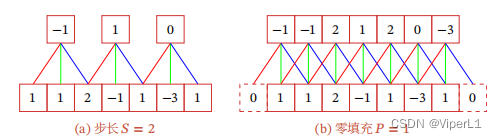
                     卷积变种的类型：

                            ①窄卷积：步长S=1，两端不补零P=0，输出长度为M-K+1

                            ②宽卷积：步长S=1，两端补零P=K-1，输出长度为M+K-1

                            ③等宽卷积：步长S=1，两端补零P=(K-1)/2，输出长度M

            2.卷积的数学性质

                    ①交换性

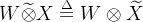
                            W \widetilde{\otimes }X\overset{\Delta}{=}W \otimes \widetilde{X}        rot180(W)\widetilde{\otimes }X=rot180(X)\widetilde{\otimes }W

                    ②导数

                            \frac{\partial f(Y)}{\partial X}=rot180(\frac{\partial f(Y)}{\partial Y})\widetilde{\otimes}W=rot180(W)\widetilde{\otimes}\frac{\partial f(Y)}{\partial Y}​​​​​​​

  • 相关阅读:
    51单片机学习/直流电机驱动
    Linux：文本处理
    利用Bootstrap的分页组件实现分页效果
    ElasticSearch - 初步检索
    uniapp学习笔记 真机运行遇到的问题
    k8s学习（RKE+k8s+rancher2.x）成长系列之简配版环境搭建（四）之Helm及cert-manager安装
    解决CubeIDE调试时函数找不到源
    LeetCode·45.跳跃游戏 ||· 贪心·动态规划
    一键自动化博客发布工具,用过的人都说好(知乎篇)
    Web前端：选择ReactJS的7个理由
  • 原文地址：https://blog.csdn.net/weixin_37878740/article/details/126665570