qlib因子分析之alphalens源码解读

百天计划第33篇，不知不觉一个多月。

"N阶行动"计划第2阶，这一阶就告诉自己要坚持，差不多可以挺过去。

坚持并不容易，早上起来心情有起伏。

投资说简单非常简单，就是低卖高卖；往难里说可能扯到宇宙星辰，人性善恶。

在量化人的眼中，一切都是因子。

技术面是因子，基本面也是因子。

有点像体验里验血、尿，B超等，给出一系列量化指标，再结合你的表述，症状，有经验的医生就可以给出结果。

当然总有很多信息是难以量化的，人是一个复杂系统。

股票也一样，所以才需要医生的存在。

量化投资本质上就是“找因子”，技术分析里可以量化的部分都是因子，因子进入模型不是hard-code的，而是以概率的形式，这就存在可以学习和优化的空间。

传统动量模型，比如20日动量>0.02就买入，小于0就卖出，和MACD>0一样，在大牛市非常好，震荡市让你怀疑人生，关键是你不知道当前是什么趋势。拉开了周期，这些因子都是alpha。

01 因子数据准备

alphalens的代码量不大，一共就4个文件：

get_clean_factor_and_forward_returns，在utils.py里。

这个函数返回如下格式的数据，它基于的输入：

因子值，这个还在下表中未动，但给因子分5层（quantile）。

基于价格prices，计算出未来1天（D）,5天和20天的收益率。

具体想计算多少天都行，用periods=(1,5,20)来设置即可。

改成periods=(1,5,10,15,20)，其实就是计算N天的预期收益率。

核心代码如下：

forward_returns = compute_forward_returns(
    factor,
    prices,
    periods,
    filter_zscore,
    cumulative_returns,
)

factor_data = get_clean_factor(factor, forward_returns, groupby=groupby,
                               groupby_labels=groupby_labels,
                               quantiles=quantiles, bins=bins,
                               binning_by_group=binning_by_group,
                               max_loss=max_loss, zero_aware=zero_aware)

compute_forward_returns就是计算“预期收益率”。

使用dataframe的 N期“变化率”，就是收益率。

for period in sorted(periods):
    if cumulative_returns:
        returns = prices.pct_change(period)

然后使用pandas的qcut函数，把因子分成5等分。

def quantile_calc(x, _quantiles, _bins, _zero_aware, _no_raise):
    try:
        if _quantiles is not None and _bins is None and not _zero_aware:
            return pd.qcut(x, _quantiles, labels=False) + 1
        elif _quantiles is not None and _bins is None and _zero_aware:
            pos_quantiles = pd.qcut(x[x >= 0], _quantiles // 2,
                                    labels=False) + _quantiles // 2 + 1
            neg_quantiles = pd.qcut(x[x < 0], _quantiles // 2,
                                    labels=False) + 1
            return pd.concat([pos_quantiles, neg_quantiles]).sort_index()
        elif _bins is not None and _quantiles is None and not _zero_aware:
            return pd.cut(x, _bins, labels=False) + 1
        elif _bins is not None and _quantiles is None and _zero_aware:
            pos_bins = pd.cut(x[x >= 0], _bins // 2,
                              labels=False) + _bins // 2 + 1
            neg_bins = pd.cut(x[x < 0], _bins // 2,
                              labels=False) + 1
            return pd.concat([pos_bins, neg_bins]).sort_index()
    except Exception as e:
        if _no_raise:
            return pd.Series(index=x.index)
        raise e

02 因子分析

create_full_tear_sheet这个函数是总体分析入口。

一共做了四件事：

统计分位表：

plotting.plot_quantile_statistics_table(factor_data)

一共就两行代码：

quantile_stats = factor_data.groupby('factor_quantile') \
    .agg(['min', 'max', 'mean', 'std', 'count'])['factor']
quantile_stats['count %'] = quantile_stats['count'] \
    / quantile_stats['count'].sum() * 100.

就是因子值，按分位分组后，计算“最小值min”,"最大值max",“均值mean”,"标准差std"。大约每个分位占20%，符合预期。

这里可能会引发一个困惑：第一分位的max不应该 <= 第二分位的min嘛 ，怎么有这么多重叠？——按天分的，每天都分5段，总体来看，就会有区间重叠。

第二步：收益分析：

create_returns_tear_sheet(
    factor_data, long_short, group_neutral, by_group, set_context=False
)

等权买入5个分位的股票后，可以计算各周期的收益率。

平均收益与分位收益之间的回归分析：

universe_ret = factor_data.groupby(level='date')[
    utils.get_forward_returns_columns(factor_data.columns)] \
    .mean().loc[returns.index]

使用线性回归OLS：

alpha_beta = pd.DataFrame()
for period in returns.columns.values:
    x = universe_ret[period].values
    y = returns[period].values

x = add_constant(x)

  reg_fit = OLS(y, x).fit()
    try:
        alpha, beta = reg_fit.params

计算出alpha和beta。

收益分析看起来有点类似“回测”，按因子高低买卖，看回测结果——结果都不错，但似乎没什么用，关键还看“信息分析”。

第三步：信息分析：

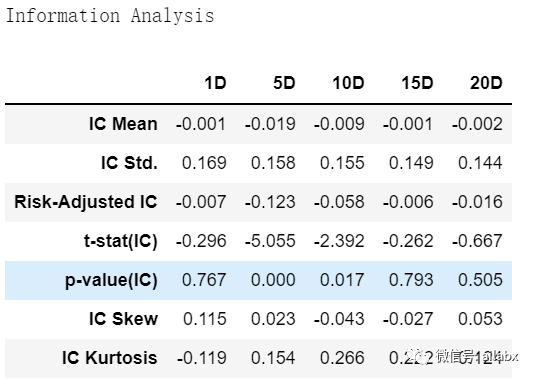
def src_ic(group):
    f = group['factor']
    _ic = group[utils.get_forward_returns_columns(factor_data.columns)] \
        .apply(lambda x: stats.spearmanr(x, f)[0])
    return _ic

IC值就是相关系数，这个之前文章说过了。

相关系数都是负的，且绝对值小于0.05，就是不显著，或者说这个因子没啥用。

第四：换手率分析：

create_turnover_tear_sheet(factor_data, set_context=False)

小结：

基本把目前传统的因子分析说完了，展开代码来看，没有什么神秘的，就是基础统计分析和线性回归。

单因子分析的逻辑是这样的，把因子从小到大分成5组，每天等权买这组，看period=1,5,10...之后的收益率情况。这是收益分析；把因子值直接与收益序列做相关性分析，得到IC值。最后交易会有换手率的问题。

最近文章：

基于alphalens对qlib的alpha158做单因子分析

人生B计划，不确定时代的应对之道

持续行动——从想到到做到

飞狐，科技公司CTO，用AI技术做量化投资；以投资视角观历史，解时事；专注个人成长与财富自由。