LeetCode220902_93、搜索二维矩阵 II

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
 

示例 1：

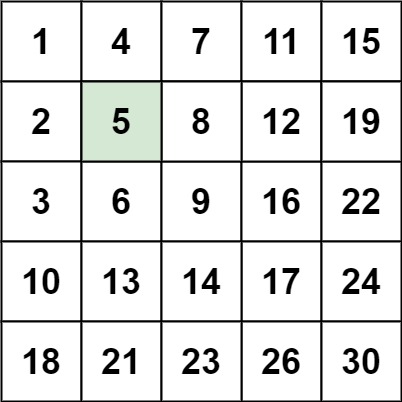
图1、 搜索二维矩阵II示例图

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/search-a-2d-matrix-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解一、有序，二分查找

①带剪枝

class Solution{
    public boolean searchMatrix(int[][] matrix, int target){
        for(int i = 0; i < matrix.length; i++){
            if(matrix[i][0] > target) break;
            else if(matrix[i][matrix[0].length - 1] < target) continue;
            int res = binarySearch(matrix[i], target);
            if(res != -1) return true;
        }
        return false;
    }
 
    public int binarySearch(int[] nums, int target){
        int left = 0;
        int right = nums.length - 1;
        while(left <= right){
            int mid = left + right >> 1;
            if(nums[mid] == target) return mid;
            else if(nums[mid] < target){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        return -1;
    }
}

② 有mid赋值left，注意mid是否需要+1

class Solution{
    public boolean searchMatrix(int[][] matrix, int target){
        for(int i = 0; i < matrix.length; i++){
            int left = 0;
            int right = matrix[0].length - 1;
            while(left < right){
                int mid = left + right + 1 >> 1;
                if(matrix[i][mid] <= target) left = mid;
                else right = mid - 1;
            }
            if(matrix[i][right] == target) return true;
        }
        return false;
    }
}

题解二、从右上角开始遍历，每次可去掉一行或一列（当前元素左边均比它小，下边均比它大）

class Solution{
    public boolean searchMatrix(int[][] matrix, int target){
        int row = 0;
        int col = matrix[0].length - 1;
        while(row < matrix.length && col >= 0){
            if(matrix[row][col] == target) return true;
            else if(matrix[row][col] < target){
                row++;
            }else{
                col--;
            }
        }
        return false;
    }
}