剑指offer62-67排序-前缀树

剑指 Offer II 062. 实现前缀树

Trie（发音类似 “try”）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

实现这种结构

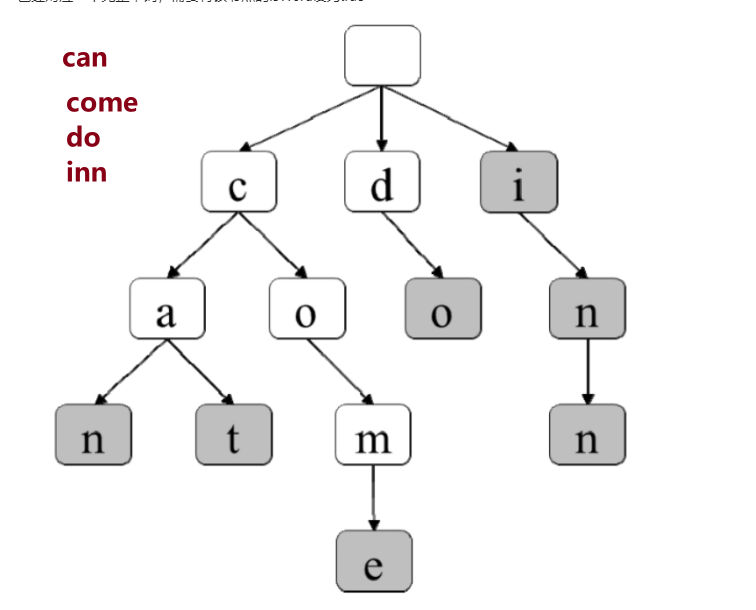
方法

定义一个类，这个类是由一个vector和isEnd组成，前者是存放26个孩子节点，后者表示单词是否已经结束

搜索前缀。比如Anthony，an就是它的一个前缀，下面方法可以检验an是否是这个单词的前缀

搜索这个单词

class Trie {
private:
    vector<Trie*> children;
    bool isEnd;

    Trie* searchPrefix(string prefix) {
        Trie* node = this;
        for (char ch : prefix) {
            ch -= 'a';
            if (node->children[ch] == nullptr) {
                return nullptr;
            }
            node = node->children[ch];
        }
        return node;
    }

public:
    Trie() : children(26), isEnd(false) {}

    void insert(string word) {
        Trie* node = this;
        for (char ch : word) {
            ch -= 'a';
            if (node->children[ch] == nullptr) {
                node->children[ch] = new Trie();
            }
            node = node->children[ch];
        }
        node->isEnd = true;
    }

    bool search(string word) {
        Trie* node = this->searchPrefix(word);
        return node != nullptr && node->isEnd;
    }

    bool startsWith(string prefix) {
        return this->searchPrefix(prefix) != nullptr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

剑指 Offer II 063. 替换单词

在英语中，有一个叫做 词根(root) 的概念，它可以跟着其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。例如，词根an，跟随着单词 other(其他)，可以形成新的单词 another(另一个)。

现在，给定一个由许多词根组成的词典和一个句子，需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根，则用最短的词根替换它。

需要输出替换之后的句子。

输入：dictionary = [“cat”,“bat”,“rat”], sentence = “the cattle was rattled by the battery”
输出：“the cat was rat by the bat”

题目意思，cattle有cat，将cattle替换成cat

方法：将给的数组插入前缀树，将句子分解为单词，逐个单词遍历前缀树

// 构造前缀树节点
class Trie {
private:
    bool isWord;
    vector<Trie*> children;
public:
    Trie () : isWord(false), children(26, nullptr) {}

    void insert(const string& str) {
        Trie* node = this;
        for (auto& ch : str) {
            if (node->children[ch - 'a'] == nullptr) {
                node->children[ch - 'a'] = new Trie();
            }
            node = node->children[ch - 'a'];
        }
        node->isWord = true;
    }

    int countPreFixLen(const string& str) {
        Trie* node = this;
        int len = 0;
        for (auto& ch : str) {
            if (node->children[ch - 'a'] == nullptr) {
                return 0;
            }
            node = node->children[ch - 'a'];
            len++;
            if (node->isWord) {
                return len;
            }
        }
        return 0;
    }
};

class Solution {
public:
    string replaceWords(vector<string>& dictionary, string sentence) {
        Trie* root = new Trie();
        for (string& word : dictionary) {
            root->insert(word);
        }
        
        // 分割
        vector<string> words{""};
        for (auto& ch : sentence) {
            if (ch != ' ') {
                words.back().push_back(ch);
            }
            else {
                words.push_back("");
            }
        }

        // 处理
        vector<string> ret;
        for (auto& word : words) {
            int len = root->countPreFixLen(word);
            if (len == 0) {
                ret.emplace_back(word);
            }
            else {
                ret.push_back(word.substr(0, len));
            }
        }

        // 拼接
        string ans{""};
        for (auto& word : ret) {
            ans += word;
            ans += " ";
        }
        ans.pop_back();

        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

剑指 Offer II 064. 神奇的字典

设计一个使用单词列表进行初始化的数据结构，单词列表中的单词 互不相同 。 如果给出一个单词，请判定能否只将这个单词中一个字母换成另一个字母，使得所形成的新单词存在于已构建的神奇字典中。

实现 MagicDictionary 类：

MagicDictionary() 初始化对象
void buildDict(String[] dictionary) 使用字符串数组 dictionary 设定该数据结构，dictionary 中的字符串互不相同
bool search(String searchWord) 给定一个字符串 searchWord ，判定能否只将字符串中 一个 字母换成另一个字母，使得所形成的新字符串能够与字典中的任一字符串匹配。如果可以，返回 true ；否则，返回 false 。

输入
inputs = [“MagicDictionary”, “buildDict”, “search”, “search”, “search”, “search”]
inputs = [[], [[“hello”, “leetcode”]], [“hello”], [“hhllo”], [“hell”], [“leetcoded”]]
输出
[null, null, false, true, false, false]

解释
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict([“hello”, “leetcode”]);
magicDictionary.search(“hello”); // 返回 False
magicDictionary.search(“hhllo”); // 将第二个 ‘h’ 替换为 ‘e’ 可以匹配 “hello” ，所以返回 True
magicDictionary.search(“hell”); // 返回 False
magicDictionary.search(“leetcoded”); // 返回 False

将一个单词替换一个字母能够匹配已经存在的单词，比如已经有了hello，将hhllo中的h替换为e便成了hello

方法 前缀树遍历遇到异常时递归

构造前缀树，定义一个全局变量edit用来表示已经容错的个数，最大是1

class Trie {
public:
    vector<Trie*> children;     //当前节点的子孩子
    bool isEndPoint;
public:
    Trie() {
        children.resize(26);
        isEndPoint = 0;
    }

    void insert(string& word)
    {
        Trie* node = this;
        for (char& ch : word)
        {
            int idx = ch - 'a';
            if (node->children[idx] == nullptr)
                node->children[idx] = new Trie();
            node = node->children[idx];
        }
        node->isEndPoint = 1;
    }
};

class MagicDictionary {
private:
    Trie* trie;
public:
    //pos为word的当前字符位置
    bool dfs(Trie* node, string& word, int pos, int& edit)
    {
        //如果找到叶子节点都没成功
        if (node == nullptr)
            return false;

        //如果刚好到达字符串末尾，且node处于根节点，且只被修改过一个字符
        if (node->isEndPoint && pos == word.length() && edit == 1)
            return true;

        if (pos != word.length() && edit <= 1)
        {
            //遍历当前节点的所有子节点，
            for (int i = 0; i < 26; ++i)
            {
                //如果子节点存在，edit不变；否则，edit加1；
                int next = (i == (word[pos] - 'a')) ? edit : edit + 1;
                if (dfs(node->children[i], word, pos + 1, next))
                    return true;
            }
        }
        return false;
    }

    /** Initialize your data structure here. */
    MagicDictionary() {
        trie = new Trie();
    }

    void buildDict(vector<string> dictionary) {
        for (string& str : dictionary)
            trie->insert(str);
    }

    bool search(string searchWord) {
        int pos = 0, edit = 0;
        return dfs(trie, searchWord, pos, edit);
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

剑指 Offer II 065. 最短的单词编码

单词数组 words 的 有效编码 由任意助记字符串 s 和下标数组 indices 组成，且满足：

words.length == indices.length
助记字符串 s 以 ‘#’ 字符结尾
对于每个下标 indices[i] ，s 的一个从 indices[i] 开始、到下一个 ‘#’ 字符结束（但不包括 ‘#’）的 子字符串 恰好与 words[i] 相等
给定一个单词数组 words ，返回成功对 words 进行编码的最小助记字符串 s 的长度 。

输入：words = [“time”, “me”, “bell”]
输出：10
解释：一组有效编码为 s = “time#bell#” 和 indices = [0, 2, 5] 。
words[0] = “time” ，s 开始于 indices[0] = 0 到下一个 ‘#’ 结束的子字符串，如加粗部分所示 “time#bell#”
words[1] = “me” ，s 开始于 indices[1] = 2 到下一个 ‘#’ 结束的子字符串，如加粗部分所示 “time#bell#”
words[2] = “bell” ，s 开始于 indices[2] = 5 到下一个 ‘#’ 结束的子字符串，如加粗部分所示 “time#bell#”

“time”, “me”, “bell” time的me和me重复，所以time ，me变为了time，time和bell没有重复，所以变为了time ，bell

方法：前缀树倒叙插入

最后统计节点的个数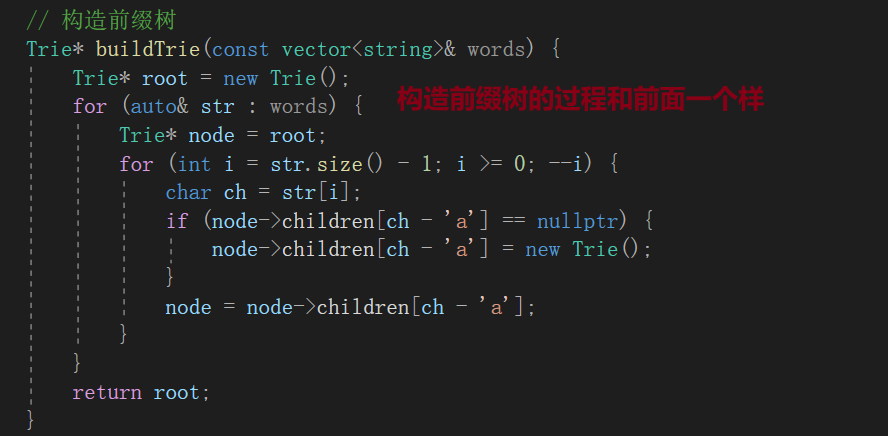

剑指 Offer II 066. 单词之和

实现一个 MapSum 类，支持两个方法，insert 和 sum：

MapSum() 初始化 MapSum 对象
void insert(String key, int val) 插入 key-val 键值对，字符串表示键 key ，整数表示值 val 。如果键 key 已经存在，那么原来的键值对将被替代成新的键值对。
int sum(string prefix) 返回所有以该前缀 prefix 开头的键 key 的值的总和。
输入：
inputs = [“MapSum”, “insert”, “sum”, “insert”, “sum”]
inputs = [[], [“apple”, 3], [“ap”], [“app”, 2], [“ap”]]
输出：
[null, null, 3, null, 5]

解释：
MapSum mapSum = new MapSum();
mapSum.insert(“apple”, 3);
mapSum.sum(“ap”); // return 3 (apple = 3)
mapSum.insert(“app”, 2);
mapSum.sum(“ap”); // return 5 (apple + app = 3 + 2 = 5)

前缀树，插入时如果分支存在则用新的值替代原来的值，sum时是计算共同前缀的和，比如求a，则将所以单词是a的单词对应的值全部计算

方法前缀树

插入

代码

// 构造前缀树节点
class Trie {
public:
    vector<Trie*> children;
    Trie() : children(26, nullptr) {}
};

// 构造前缀树节点
class Trie {
public:
    int val;
    vector<Trie*> children;
    Trie() : val(0), children(26, nullptr) {}

    // 实现插入字符串
    void insert(string& str, int m) {
        Trie* node = this;
        for (auto& ch : str) {
            if (node->children[ch - 'a'] == nullptr) {
                node->children[ch - 'a'] = new Trie();
            }
            node = node->children[ch - 'a'];
        }
        node->val = m;
    }

    // 实现返回所有以该前缀 prefix 开头的键 key 的值的总和
    int coutSum(string& prefix) {
        Trie* node = this;
        for (auto& ch : prefix) {
            if (node->children[ch - 'a'] == nullptr) {
                return 0;
            }
            node = node->children[ch - 'a'];
        }

        // BFS
        int count = 0;
        queue<Trie*> que;
        que.push(node);
        while (!que.empty()) {
            Trie* node = que.front();
            que.pop();
            count += node->val;
            for (int i = 0; i < node->children.size(); ++i) {
                if (node->children[i] != nullptr) {
                    que.push(node->children[i]);
                }
            }
        }
        return count;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

剑指 Offer II 067. 最大的异或

给定一个整数数组 nums ，返回 nums[i] XOR nums[j] 的最大运算结果，其中 0 ≤ i ≤ j < n 。
输入：nums = [3,10,5,25,2,8]
输出：28
解释：最大运算结果是 5 XOR 25 = 28.

方法：前缀找相反位