《算法图解》阅读笔记

第一章

以猜数引入二分查找

对于猜数，如果从1开始猜，会猜n次，但是对于二分而言，只需猜log n次，比方说如果最大数是240000，那么对于n要猜240000，但是对于二分只需要猜18次！

• 算法的速度指的并非时间，而是操作数的增速。谈论算法的速度时，我们说的是随着输入的增加，其运行时间将以什么样的速度增加。
• 算法的运行时间用大O表示法表示。 O(log n)比O(n)快，当需要搜索的元素越多时，前者比后者快得越多。 算法运行时间并不以秒为单位。
• 算法运行时间是从其增速的角度度量的。

第二章 选择排序

内容有 数组和链表

第三章 递归

如果使用循环，程序的性能可能更高；如果使用递归，程序可能 更容易理解。如何选择要看什么对你来说更重要

当用到递归的时候，我希望能想到下面这个例子：
祖母告诉你有一个上锁的神秘手提箱，而钥匙很可能在下面这个盒子里。这个盒子里有盒子，而盒子里的盒子又有盒子。钥匙就在某个盒子中。

为了找到钥匙，创建一个待查找的盒子堆，因此你始终知道还有哪些盒子需要查找，但是

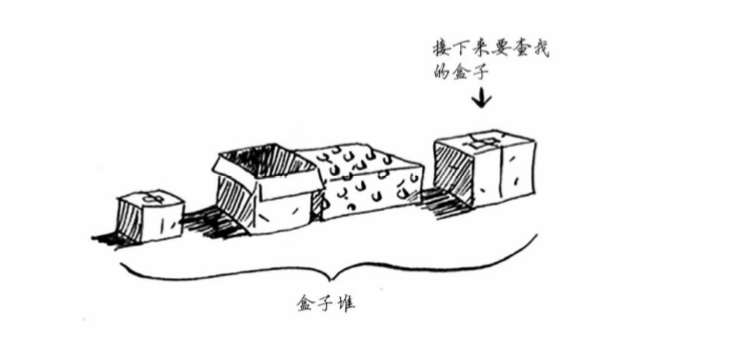
但是在递归里面，并没有盒子堆，那么如果确定呢，下面是一个例子

此时调用栈如下：

可以看到，“盒子堆”存储在了栈中！这个栈包含未完成的函数调用，每个函数调用都包含还未检查完的盒子。使用栈很方便，因为你无需自己跟踪盒子堆——栈替你这样做了。
希望在每次使用递归的时候都能想起上面的内容

每个递归函数都有两部分：基线条件和递归条件。
递归条件指的是函数调用自己，而基线条件则指的是函数不再调用自己，从而避免形成无限循环。

每个函数调用都要占用一定的内存，如果栈很高，就意味着计算机存储了大量函数调用的信息。在这种情况 下，有两种选择：
1、重新编写代码，转而使用循环。
2、使用尾递归。这是一个高级递归主题，但并非所有的语言 都支持尾递归。

尾递归简要介绍

在传统的递归中，典型的模型是首先执行递归调用，然后获取递归调用的返回值并计算结果。以这种方式，在每次递归调用返回之前，您不会得到计算结果。

假设你调用greet(“maggie”)，计算机将首先为该函数调用分配一块内存。

我们来使用这些内存。变量name被设置为maggie，这需要存储到内存中

如果调用函数的话，计算机也为这个函数调用分配一 块内存。

当函数调用完成，栈顶的内存块会被弹出

调用另一个函数时，当前函数暂停 并处于未完成状态。该函数的所有变量的值都还在内存中。执行完函数greet2后，你回到函数 greet，并从离开的地方开始接着往下执行
这个栈用于存储多个函数的变量，被称为调用栈。

所以它的缺点是：

• 效率低，占内存
• 如果递归链过长，可能会statck overflow

若函数在尾位置调用自身（或是一个尾调用本身的其他函数等等），则称这种情况为尾递归。尾递归也是递归的一种特殊情形。

当编译器检测到一个函数调用是尾递归的时候，它就覆盖当前的活动记录而不是在栈中去创建一个新的。编译器可以做到这点，因为递归调用是当前活跃期内最后一条待执行的语句，于是当这个调用返回时栈帧中并没有其他事情可做，因此也就没有保存栈帧的必要了。通过覆盖当前的栈帧而不是在其之上重新添加一个，这样所使用的栈空间就大大缩减了，这使得实际的运行效率会变得更高。

第四章 快速排序

递归的深入

1、分而治之（divide and conquer，D&C）（D&C策略）

适用于这小块地的最大方块，也是适用于整块地的最大方块-—适合某个阶段的最好结果，就是适合整个阶段的最好结果

有个简单的农场主问题，大概意思就是在一块地中分成n块尽可能大的土地，这里不加以介绍，以另一个例子展开，求解一个数组的和：

• 第一步：找出基线条件，最简单的数组是–如果数组不包含任何元素或只包含一个元素，那么就
• 第一步：每次递归调用都必须离空数组更近一步。也就是缩小问题的规模，或者说找出当前的最好情况
  比如，如果sum是递归函数，sum([1,2,3]),那么进入以后1+sum([2,3])就是缩小了问题的规模
  

编写涉及数组的递归函数时，基线条件通常是数组为空或只包含一个元素。陷入困境时， 请检查基线条件是不是这样的

分而治之的实例——快速排序

数据结构内容，将第一个元素作为基准值，将左边的都变为比其小，将右边的都变为比右边大

• 第一步，确定基线条件，一个数组基线条件通常为空或者包含一个元素，那么此时直接返回这个数组就可以了
• 第二步，缩小问题的规模或者找出当前问题的最好情况
  当前问题所能做的就是让基准值的左边都比它更小，让其右边都比其大

可以说，这样将问题全部考虑了，也就是基线条件对空数组或包含一个 元素的数组管用，而在缩小规模或者叫当前最好情况条件中，我证明如果快速排序对包含一个元素的数组管用，对包含两 个元素的数组也将管用；如果它对包含两个元素的数组管用，对包含三个元素的数组也将管用， 以此类推。因此，我可以说，快速排序对任何长度的数组都管用。

第五章 散列函数

     散列表的查找的时间复杂度为O(1)

     散列函数：将输入映射到数字

     散列函数必须满足一些要求：
     （1）它必须是一致的，例如输入apple得到4，那么每次输入apple，都要得到4.
     （2）它应将不同的输入映射到不同的数字。
1
2
3
4
5
6
7

散列表的应用
1、将散列表用于查找
2、防止重复
3、将散列表用于缓存

第六章 广度有限搜索

广度优先搜索是一种用于图的查找算法，可帮助回答两类问题：
第一类问题：从节点A出发，有前往节点B的路径吗？
第二类问题：从节点A出发，前往节点B的哪条路径最短？

第一类问题：有路径吗

假设你经营着一个芒果农场，需要寻找芒果销售商，以便将芒果卖给他
在你看来，一度关系胜过二度关系，二度关系胜过三度关系，以此类推。因此，你应先在一 度关系中搜索，确定其中没有芒果销售商后，才在二度关系中搜索

那么第一轮先问一圈朋友，问与芒果销售商有联系吗？如果都没有，
那么第二轮问一圈朋友的朋友，问与芒果销售商有联系吗？如果都没有，
那么第三轮问一圈朋友的朋友的朋友，以此类推

这就是广度优先搜索算法

第二类问题：最短路径是多少

广度优先会扫描出最短路径，因为关系是从一度关系中开始的，直到找到销售商

第七章 狄克斯特拉算法

狄克斯特拉算法只适用于有向无环图

第八章 贪婪算法

没有快速算法的问题（NP完全问题）。
要识别NP完全问题，以免浪费时间去寻找解决它们的快速算法。
要学习近似算法，使用它们可快速找到NP完全问题的近似解。

1、教室调度问题

你希望将尽可能多的课程安排在某间教室上，也即在这间教室上尽可能多的课。看着貌似很复杂，但是算法可能简单得让你大吃一惊。

具体做法如下。
(1) 选出结束最早的课，它就是要在这间教室上的第一堂课。
(2) 接下来，必须选择第一堂课结束后才开始的课。同样，你选择结束最早的课，这将是要 在这间教室上的第二堂课。 重复这样做就能找出答案！

这就是贪婪算法，贪婪算法很简单：每步都采取最优的做法。用专业术语说，就是你每步都选择局部最优解，最终得到的就是全局最优解
贪婪算法的整理 ：贪婪算法整理

如果用贪婪算法解决背包问题：
(1) 盗窃可装入背包的最贵商品。
(2) 再盗窃还可装入背包的最贵商品，以此类推。
只是这次这种贪婪策略不好使了！

你的背包可装35磅的东西。音响最贵，你把它给偷了，但背包没有空间装其他东西了。

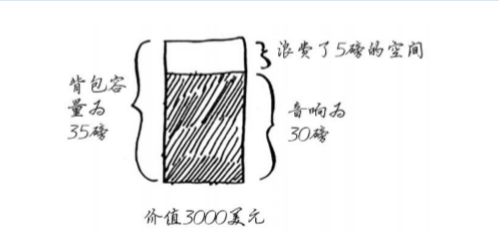
你偷到了价值3000美元的东西。且慢！如果不是偷音响，而是偷笔记本电脑和吉他，总价将 为3500美元！

在这里，贪婪策略显然不能获得最优解，但非常接近。从这个示例你得到了如下启示：**在有些情况下，完美是优秀的敌人。**有时候，你只需找到一 个能够大致解决问题的算法，此时贪婪算法正好可派上用场，因为它们实现起来很容易，得到的 结果又与正确结果相当接近。

2、集合覆盖问题

假设你办了个广播节目，要让全美50个州的听众都收听得到。为 此，你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用，但是广播台覆盖的有重叠，因此你力图在尽可能少的广播台播出。如何找出覆盖全美50个州的最小广播台集合呢？

最笨的一个方法：
(1) 列出每个可能的广播台集合，这被称为幂集（power set）。可能的子集有2n个。
(2) 在这些集合中，选出覆盖全美50个州的最小集合。

如果广播台很多，需要的时间将激增，假设你每秒可计算10个子集，那么没有任何算法可以足够快地解决这个问题。

贪婪算法可化解危机！使用下面的贪婪算法可得到非常接近的解。
(1) 选出这样一个广播台，即它覆盖了最多的未覆盖州。即便这个广播台覆盖了一些已覆盖 的州，也没有关系。
(2) 重复第一步，直到覆盖了所有的州。

在这个例子中，贪婪算法 的运行时间为O(n2)

判断近似算法优劣的标准如下：

• 速度有多快；
• 得到的近似解与最优解的接近程度

3、NP完全问题

为解决集合覆盖问题，你必须计算每个可能的集合。 也就是穷举所有的可能，然后作比较。
旅行商问题和集合覆盖问题有一些共同之处：你需要计算所有的解，并从中选出最小/最短 的那个。这两个问题都属于NP完全问题。
NP完全问题的简单定义是，以难解著称的问题，如旅行商问题和集合覆盖问题。很多非常 聪明的人都认为，根本不可能编写出可快速解决这些问题的算法。

如何识别NP完全问题

Jonah正为其虚构的橄榄球队挑选队员。他列了一个清单，指出了对球 队的要求：优秀的四分卫，优秀的跑卫，擅长雨中作战，以及能承受压力 等。他有一个候选球员名单，其中每个球员都满足某些要求。

如果你想组建一个满足所有这些要求的球队，可名额有限。但这就是覆盖问题啊

可以使用贪婪算法来组建球队
(1) 找出符合最多要求的球员。
(2) 不断重复这个过程，直到球队满足要求（或球队名额已满）。

NP问题的特点

• 元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
• 涉及“所有组合”的问题通常是NP完全问题。
• 不能将问题分成小问题，必须考虑各种可能的情况。这可能是NP完全问题。
• 如果问题涉及序列（如旅行商问题中的城市序列）且难以解决，它可能就是NP完全问题。
• 如果问题涉及集合（如广播台集合）且难以解决，它可能就是NP完全问题。
• 如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题。