• 计算机智能专题-遗传算法(1不带约束的)

    前言：

             遗传算法是一种群智能优化算法，它主要解决的是排列组合问题。通过模仿遗传学中染色体的交叉、变异、并通过“优选”，使父代产生更优的“子代”，在不断的“优胜略汰”中，最终得到最优的组合。更新ing，，，，

    本篇文章讲的是：遗传算法的整数编码，原理较为简单可以用作入门。

    第二篇遗传算法“实数编码”，是模仿二进制交叉和编译，适用范围更广泛。

    一、基本概念

    1.编码：

    >>生物学定义：DNA中遗传信息在一个长链上按一定的模式排列

    >>计算机学定义：将实际问题抽象成"染色体",所建立的数学模型，具体来讲，实际问题中的排列组合问题，并不是涉及染色体，要使用遗传算法解决问题需要进行模型转化。

    2.解码：

    >>生物学定义: 从遗传DNA到表现型的映射

    >>计算机学定义：实际问题通过“编码”过程映射为染色体并使用遗产算法处理之后，需要重新映射到实际问题中，来获得真实的自由组合，这个过程叫做解码。

    3.交叉

    >>生物学定义：在两个染色体的某一相同位置处DNA被切断，其前后两串分别交叉组合形成两个新的染色体。

    >>计算机学定义：在实际的操作中会模仿这样的操作，对编码后的数据进行交叉。

    4.变异:

    >>生物学定义：很小概率产生基因突变，产生出新的染色体，然后表现出新的性状

    5.适应度

    度量某个物种对于生存环境的适应程度。对于生存化境适应程度较高的物种将获得更多的繁殖机会，反之机会较少，甚至灭绝。

    6.选择

    指定以一定的概率从种群中选择若干个体进行"优胜略汰"。

    二、基本流程

     三、具体实例

    3.1一个连续问题的实列

    实现遗传算法求解：

    (x−5)(x−10)(x−6)(x−16)+21

    =-x^4+37*x^3-476*x^2+2540*x-4779

    的最大值，其中x为0到31之间的整数，
    f = lambda x:-x**4+37*x**3-476*x**2+2540*x-4779

    函数图像如下图所示：

    这里做下说明，对于给出的这个实际问题，可以通过遍历循环得到0到31中满足要求的值，这里通过简单的示例，解释用遗传算法解决这个问题。

    1. 参数初始化

    >>遗传算法进化迭代次数epochs，这个根据遗传算迭代收敛的情况而定。

    >>种群个体数N，设N=8。这个根据经验设置，作为超参数调试。

    >>个体的编码长度M=5，这个根据实际问题的需要求而来，一般设置为最少能够用二进制表示的数码范围。[0,31]32位<=2^{5}.

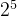    2. 种群初始化

    这里已经隐含了编码过程，十进制到二进制。

    对于这个编码过程做简单的解释：

    后面的遗传算法使用，需要进行染色体的交叉、编译操作，而二进制作为和染色体DNA最接近的数制要比十进制更符合操作习惯，将十进制转化为二进制后，二进制的每一位代表一个染色片段，而“交叉”“变异”的操作是以染色体片段为单位进行的。下面结合一个例子讲解种群初始化的过程。

    初始化代码如下，产生一个N*M的矩阵，每一行代表一个个体。

    1.     def __init__(self,N=8,M=5):
    2.         _groups = np.zeros([N,M],int)
    3.         for index in range(0,N):
    4.             for _index in range(0,M):
    5.                 _groups[index,_index] = np.random.choice([0,1])
    6.         self._groups = _groups

    说明：

     在这N*M的矩阵中，每一行是一个1*M的向量，这代表一个十进制个体的二进制表示。所以后面应用时还需要设计一个解码器，以便经过遗传算法操作过后的染色体编码可以映射到实际问题中，

    这里的解码器，是将二进制转化为十进制的函数：Binary2Decimal

    1.     def Binary2Decimal(self,Binary,include_negative=False):
    2.         '''
    3.         fct: 将二进制转化为十进制
    4.         :param Binary: 输入的二进制数组
    5.         :param include_negative: 最高位是不是 符号位
    6.         :return:
    7.         '''
    8.         sum = 0
    9.         bit_flag = -1 if include_negative==True else 1
    10.         for index in range(1,len(Binary)):
    11.             sum = sum + Binary[-index]*2**(index-1)
    12.         if  bit_flag==-1:
    13.             if Binary[0]==1:
    14.                sum = sum * bit_flag
    15.             else:
    16.                sum = sum + 0
    17.         else:
    18.             sum = sum + Binary[0]*2**(index)
    19.  
    20.         return sum

    3. 优选

            优选的方法有很多，本文中的问题是：求函数的最大值，所以优化的对象是函数值，最简单的方案是：比较种群中个体间的函数值的大小，根据值的大小进行优胜略汰。

    具体的分析：

    计算得到的值存在几种情况：

    1.全为正、2.全为负、3.有正有负、4.值一样

    优选的方式需要考虑这几种情况，通常常用的几种优选的方式有:“赌轮盘”、“锦标赛”、“小生境”

    >>赌轮盘：2021.12.23晚上更新一点

    按照某个标准，计算得到每一个个体的得分，然后将每个个体分布在一个圆盘上面，个体所占圆心角的大小取决于个体得分所占总分的比例。

     这样盘的模型就制作好了，接下来就按照“运气”进行筛选。转动红色的指针，指针指到哪里，哪一个个体就被"优选"到下一个轮回。一般需要筛选出几个个体，就转几次轮盘。

    这样做的理论依据：

            可以通过设置 评价函数 ，使较优的值的评价分数较高，这样相应的它在轮盘中所占的圆心角就越大，被选择的机会就越大，参与繁殖的机会就越大，这也符合自然法则中的优胜略汰。但是通过这种转轮盘的方式，没有直接选择最好的那一个，也给了劣势群体的一些机会，说不定有些：个体的得分不高，但是他的后代可能产生更优的性状，这种几率发生的比较低，但也是自然法则中的一个现象，所以赌轮盘这种优选方式需要考虑这种情况。

    赌轮盘制作函数：

    1.将初始化的二进制值，通过函数Binary2Decimal转化为十进制

    2.十进制直接计算得到函数值

    3. 拿着所有值减去最小值，并加以上一个数

    4. 计算所有的个体的的占比，用于制作轮盘

    1.     def calculate_suitability(self,input,error=0.01):
    2.         y_get = list(map(lambda x:f(x),input))
    3.         y_get_ = y_get-np.min(y_get)+error #让最小的那个数值 不为零
    4.         out_data = [y_get__/np.sum(y_get_) for y_get__ in y_get_]
    5.         return out_data

    摇轮盘函数：

            这个函数自行理解，关于需要优选的次数：为了保证后代的种群的数量保持不变，所以有几个个体就需要摇几次。当然个体所占圆心角较大的被优选的机会更多，可以是一个个体被多次优选到。

    1.     def optimize_choose(self,input_Data):
    2.         out_data_index = []
    3.         for index in range(len(input_Data)):         # 需要优选的次数
    4.             random_value = np.random.rand(1)         # 随机轮盘指针位置
    5.             sum_value = 0
    6.             for _index in range(len(input_Data)):    # 手动转到对应位置
    7.                 sum_value = sum_value + input_Data[_index]
    8.                 if random_value <= sum_value:
    9.                     out_data_index.append(_index)
    10.                     break
    11.                 else:
    12.                     continue
    13.         return out_data_index

     >>锦标赛：2021.12.24早上更新一点

            锦标赛制，保留最好的那个一个，或者择优录取，是人类绝大数情况下进行社交活动中所采用的较为公平的优选方式，是否得到“优选”，完全取决于个体的实力，而不考虑个体的社会关系。一般的做法，将个体按照评价标准进行打分，按照打分从高到低排序，然后“优选”取前N个个体。

    >>"小生境"：

    小生境优选，可以说综合了赌轮盘和锦标赛，考虑个体在种群中的“社会关系”，避免陷入局部最优。这个后面有机会，单独开一个博客来讲。

    4. 交叉-变异 (2021.12.27更新)

    后代之间的基因融合(交叉、变异)的基本原理如下图所示。

     这里是简单的原理描述，一些超参数的设置解释如下：

    1. 关于交叉的起始位置一般是随机的，通过设置随机函数来实现

    2. 关于交叉的长度也可以按照经验来指定，或者如上图所示的

    3. 值得注意的是：交叉规则也完全可以由经验来设计

    4. 关于变异的位置，这里也采用随机的位置。

    5. 变异的长度一般是一位

    6.交叉是子代之间一定进行的，但是变异却是按照概率发生的。

    一个具体的交叉变异函数代码如下：

    1.     def cross_variation(self,last_groups, opt_chose):
    2.         '''
    3.         :fct 对优选的后代进行交叉、变异
    4.         :param last_groups: 上一代种群中的所有个体
    5.         :param opt_chose: 经过优选 算法产生的"优秀个体的索引"，
    6.                           用于从上一代种群中筛选出优秀的个体进行下一步的繁殖
    7.         :return:进行交叉变异后的下一代
    8.         '''
    9.         opt_chose_data = [] # 优选的后的结果
    10.         for opt_flag in opt_chose:
    11.             opt_chose_data.append(last_groups[opt_flag,:])
    12.         cross_Data = copy.deepcopy(opt_chose_data)
    13.  
    14.         # 分组 因为交叉和变异，需要两两进行，所以要进行分组
    15.         index_groups = list(range(0,len(last_groups)))
    16.         np.random.shuffle(index_groups) #分组是随机的，按顺序排完之后，再次打乱
    17.  
    18.         # 染色体 交叉，
    19.         # 1. 交叉的位置是随机的
    20.         for index in range(0,int(len(index_groups)/2)):
    21.             index = index*2
    22.             # 交叉的起始位置 是随机的
    23.             variation_site = np.random.choice(list(range(0,np.shape(last_groups)[-1]))[1:]) 
    24.             variation_data = opt_chose_data[index_groups[index]][variation_site:] # 保存 中间变量
    25.             cross_Data[index_groups[index]][variation_site:] = opt_chose_data[index_groups[index+1]][variation_site:]
    26.             cross_Data[index_groups[index + 1]][variation_site:] = variation_data
    27.  
    28.         # 染色体 变异
    29.         # 2. 变异是否 发生是随机的
    30.         variation_Data = copy.deepcopy(cross_Data)
    31.         variation_value = 1/np.shape(last_groups)[-1]  #变异发生的概率
    32.         for index in range(len(variation_Data)):
    33.             variation_random_value = np.random.rand(1) #当前变异发生的概率
    34.             if variation_random_value>=variation_value:
    35.                # 变异发生的位置
    36.                variation_site = np.random.choice(list(range(0, np.shape(last_groups)[-1]))[1:]) 
    37.                # 变异的表示：0->1: 1->0
    38.                variation_Data[index][variation_site] = 1 - variation_Data[index][variation_site]
    39.  
    40.         return np.array(variation_Data)

    该函数中做一下解释：

    关于变异的发生概率一般设置为染色体长度的倒数，在繁殖中，会产生一个随机数，若随机数的概率大于变异发生概率时，就让其变异。

    5. 遗传循环

    遗传循环：包括以下几个步骤

    >>解码

    >>计算生存适应度

    >>优选

    >>交叉、变异

    >>解码,求输出值

    函数如下：

    1.     def run(self):
    2.         init_groups = self._groups
    3.         data_collect = []
    4.         for epochs in range(100):
    5.  
    6.             y_group = [self.Binary2Decimal(Binary,False) for Binary in init_groups]
    7.             y_suit = self.calculate_suitability(y_group)
    8.             opt_chose = self.optimize_choose(y_suit)
    9.  
    10.             cross_variation_data = self.cross_variation(init_groups, opt_chose)
    11.  
    12.             init_groups = copy.deepcopy(cross_variation_data)
    13.  
    14.             y_get = list(map(lambda x: f(self.Binary2Decimal(x,True)), init_groups))
    15.             data_collect.append(np.max(y_get))
    16.             print('epoch: %d 当前最优值为%f'%(epochs,np.max(data_collect)))

    结果

    汇总代码：

    1. import numpy as np
    2. import copy
    3.  
    4. '''目标函数'''
    5.  
    6. # f = lambda x:−x^4+37x^3−476x^2+2540x−4779  −(x−5)(x−10)(x−6)(x−16)+21
    7. f = lambda x:-x**4+37*x**3-476*x**2+2540*x-4779
    8.  
    9. class genetic_algorithms():
    10.     def __init__(self,N=8,M=5):
    11.         _groups = np.zeros([N,M],int)
    12.         for index in range(0,N):
    13.             for _index in range(0,M):
    14.                 _groups[index,_index] = np.random.choice([0,1])
    15.         self._groups = _groups
    16.  
    17.     def Binary2Decimal(self,Binary,include_negative=False):
    18.         '''
    19.         fct: 将二进制转化为十进制
    20.         :param Binary: 输入的二进制数组
    21.         :param include_negative: 最高位是不是 符号位
    22.         :return:
    23.         '''
    24.         sum = 0
    25.         bit_flag = -1 if include_negative==True else 1
    26.         for index in range(1,len(Binary)):
    27.             sum = sum + Binary[-index]*2**(index-1)
    28.         if  bit_flag==-1:
    29.             if Binary[0]==1:
    30.                sum = sum * bit_flag
    31.             else:
    32.                sum = sum + 0
    33.         else:
    34.             sum = sum + Binary[0]*2**(index)
    35.  
    36.         return sum
    37.  
    38.  
    39.     # 适宜度的设计 很重要
    40.     # 会出现负数，负数怎么处理
    41.     # 这里将 负数变成正数 进行处理
    42.     def calculate_suitability(self,input,error=0.01):
    43.         y_get = list(map(lambda x:f(x),input))
    44.         y_get_ = y_get-np.min(y_get)+error #让最小的那个数值 不为零
    45.         out_data = [y_get__/np.sum(y_get_) for y_get__ in y_get_]
    46.         return out_data
    47.  
    48.  
    49.     def optimize_choose(self,input_Data):
    50.         out_data_index = []
    51.         for index in range(len(input_Data)):         # 需要优选的次数
    52.             random_value = np.random.rand(1)         # 随机轮盘指针位置
    53.             sum_value = 0
    54.             for _index in range(len(input_Data)):    # 手动转到对应位置
    55.                 sum_value = sum_value + input_Data[_index]
    56.                 if random_value <= sum_value:
    57.                     out_data_index.append(_index)
    58.                     break
    59.                 else:
    60.                     continue
    61.         return out_data_index
    62.  
    63.     def cross_variation(self,last_groups, opt_chose):
    64.         '''
    65.         :fct 对优选的后代进行交叉、变异
    66.         :param last_groups: 上一代种群中的所有个体
    67.         :param opt_chose: 经过优选 算法产生的"优秀个体的索引"，
    68.                           用于从上一代种群中筛选出优秀的个体进行下一步的繁殖
    69.         :return:进行交叉变异后的下一代
    70.         '''
    71.         opt_chose_data = [] # 优选的后的结果
    72.         for opt_flag in opt_chose:
    73.             opt_chose_data.append(last_groups[opt_flag,:])
    74.         cross_Data = copy.deepcopy(opt_chose_data)
    75.  
    76.         # 分组 因为交叉和变异，需要两两进行，所以要进行分组
    77.         index_groups = list(range(0,len(last_groups)))
    78.         np.random.shuffle(index_groups) #分组是随机的，按顺序排完之后，再次打乱
    79.  
    80.         # 染色体 交叉，
    81.         # 1. 交叉的位置是随机的
    82.         for index in range(0,int(len(index_groups)/2)):
    83.             index = index*2
    84.             # 交叉的起始位置 是随机的
    85.             variation_site = np.random.choice(list(range(0,np.shape(last_groups)[-1]))[1:])
    86.             variation_data = opt_chose_data[index_groups[index]][variation_site:] # 保存 中间变量
    87.             cross_Data[index_groups[index]][variation_site:] = opt_chose_data[index_groups[index+1]][variation_site:]
    88.             cross_Data[index_groups[index + 1]][variation_site:] = variation_data
    89.  
    90.         # 染色体 变异
    91.         # 2. 变异是否 发生是随机的
    92.         variation_Data = copy.deepcopy(cross_Data)
    93.         variation_value = 1/np.shape(last_groups)[-1]  #变异发生的概率
    94.         for index in range(len(variation_Data)):
    95.             variation_random_value = np.random.rand(1) #当前变异发生的概率
    96.             if variation_random_value>=variation_value:
    97.                # 变异发生的位置
    98.                variation_site = np.random.choice(list(range(0, np.shape(last_groups)[-1]))[1:])
    99.                # 变异的表示：0->1: 1->0
    100.                variation_Data[index][variation_site] = 1 - variation_Data[index][variation_site]
    101.  
    102.         return np.array(variation_Data)
    103.  
    104.     def run(self):
    105.         init_groups = self._groups
    106.         data_collect = []
    107.         for epochs in range(100):
    108.  
    109.             y_group = [self.Binary2Decimal(Binary,False) for Binary in init_groups]
    110.             y_suit = self.calculate_suitability(y_group)
    111.             opt_chose = self.optimize_choose(y_suit)
    112.  
    113.             cross_variation_data = self.cross_variation(init_groups, opt_chose)
    114.  
    115.             init_groups = copy.deepcopy(cross_variation_data)
    116.  
    117.             y_get = list(map(lambda x: f(self.Binary2Decimal(x,True)), init_groups))
    118.             data_collect.append(np.max(y_get))
    119.             print('epoch: %d 当前最优值为%f'%(epochs,np.max(data_collect)))
    120.             # print('epoch: %d 当前最优值为%f'%(epochs,np.max(y_get)))
    121.  
    122. if __name__=='__main__':
    123.     obj = genetic_algorithms(N=8,M=5)
    124.     obj.run()

  • 相关阅读:
    1.1_4操作系统的运行机制与体系结构
    云计算对象存储服务
    ASP.NET Core 6.0对热重载的支持
    Algorithm Review 5
    【Vue域名动态配置】
    机器人过程自动化(RPA)入门 3. 顺序、流程图和控制流程
    Spring Boot 自动注入失败的原因
    【排序14：存在重复元素】
    linux部署Django项目
    Python大作业——爬虫+可视化+数据分析+数据库（可视化篇）
  • 原文地址：https://blog.csdn.net/weixin_44503976/article/details/126654578