-
数据结构之图
1.图的定义
(1)图是一种网状数据结构,图是由非空的顶点集合和一个描述顶点之间关系的集合组成.
(2)其形式化的定义如下:Graph = (V,E)

(3)加权图
①在实际应用中,图不但需要表示元素之间是否存在某种关系,而且图的边往往与具有一定实际意义的数有关,即每条边都有与它相关的实数,称为权
②这些权值可以表示从一个顶点到另一个顶点的距离或消耗等信息。这种边上具有权值的图称为带权图

2.图的存储
(1)邻接矩阵:二维数组 ,顺序结构
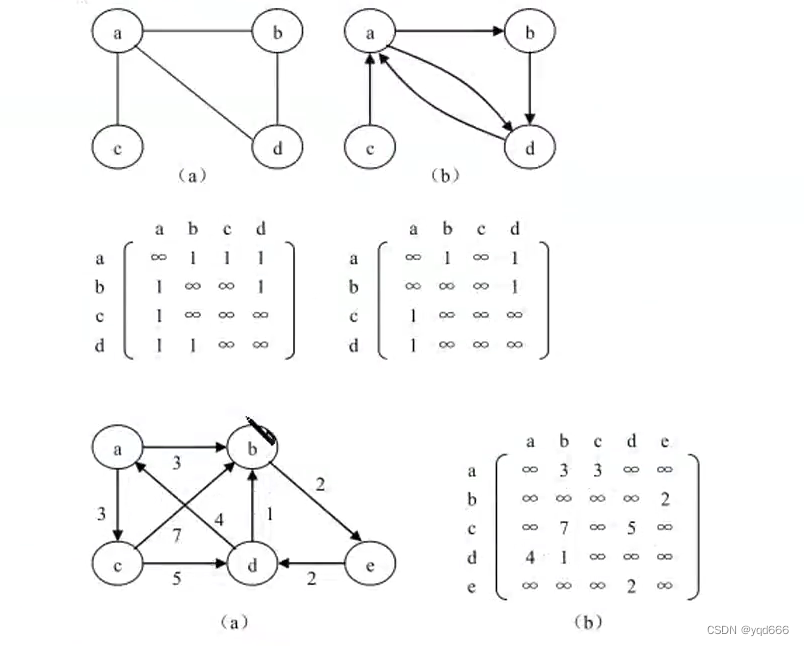
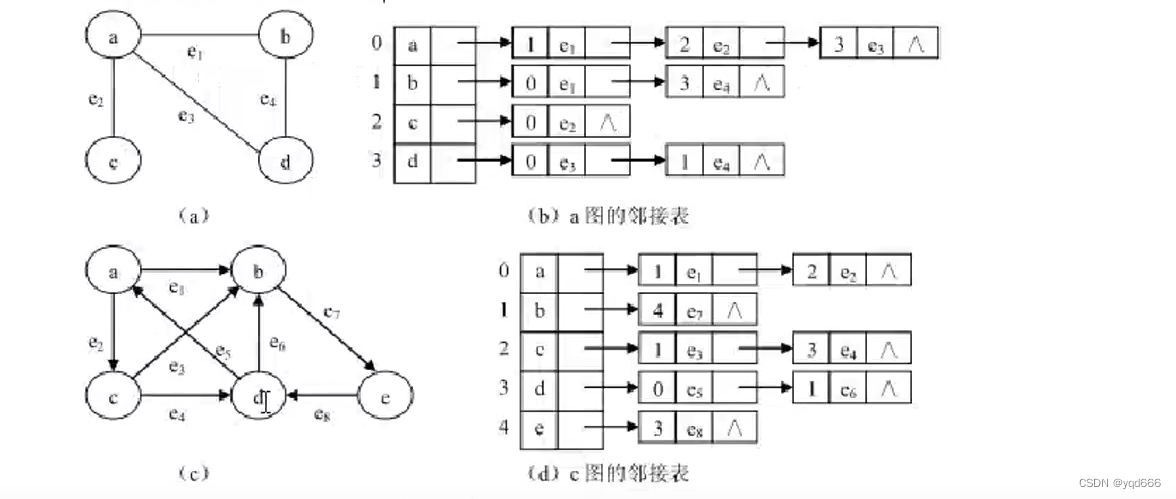
(2)邻接表:链表,链式存储结构
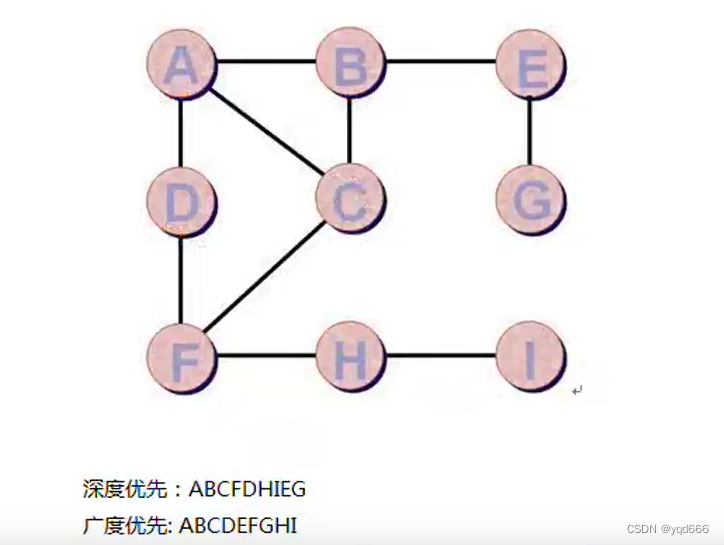
3.图的遍历
图的遍历就是从图中某个顶点出发,按某种方法对图中所有顶点访问且仅访问一次。
图的遍历算法是求解图的连通性问题、拓扑排序和求关键路径等算法的基础。
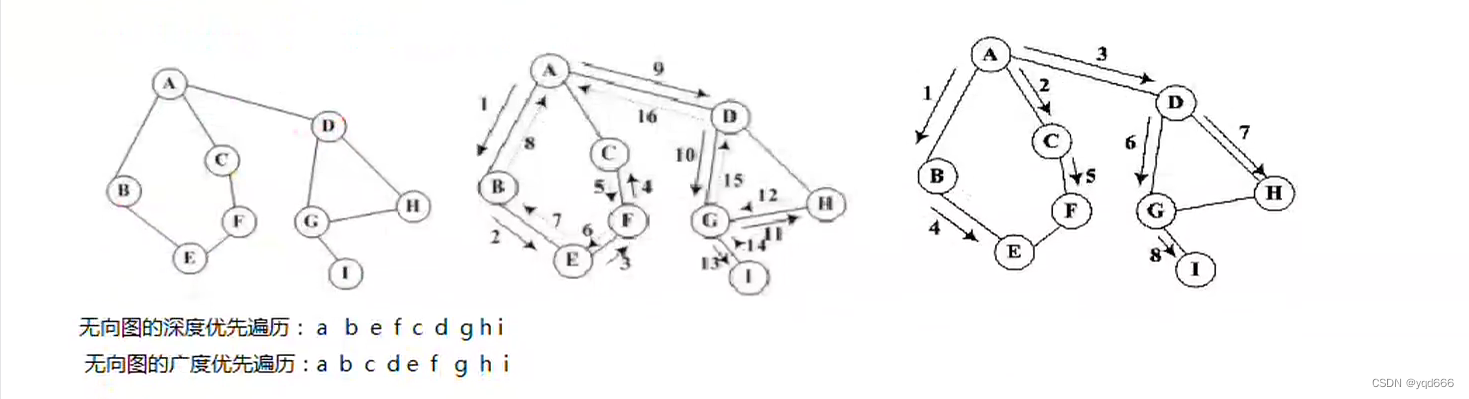
(1)深度优先遍历:类似于树的先根遍历,是树的先根遍历的推广(可以采用递归和借助栈的非递归方式实现)
(2)广度优先遍历:类似于树的层次,它是树的按层遍历的推广(借助队列、非递归方式实现)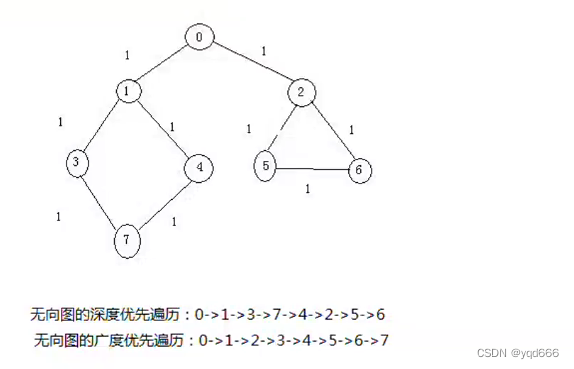
4.最短路径
在许多应用领域,带权图都被用来描述某个网络,比如通信网络、交通网络等。这种情况下,各边的权重就对应于两点之间通信的成本或交通费用。此时,一类典型的问题就是:在任意指定的两点之间如果存在通路,那么最小的消耗是多少。这类问题实际上就是带权图中两点之间最短路径的问题。
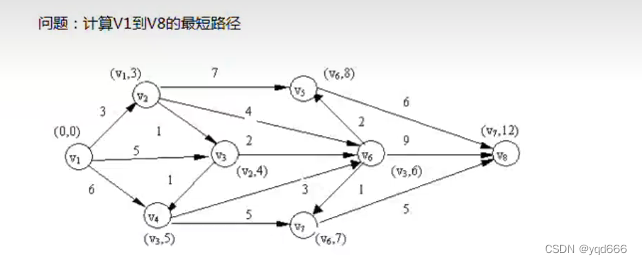
(1)最短路径1:段数最少的最短路径
生活案例:换乘最少
解决方案:使用广度优先搜索即可
类似于树的层次遍历,需要借助于队列来实现
(2)最短路径2:权值最小的最短路径
生活案例:时间最少,距离最短
解决方案:使用狄克斯特拉算法
注意:-1 表示无穷大
①从V1出发

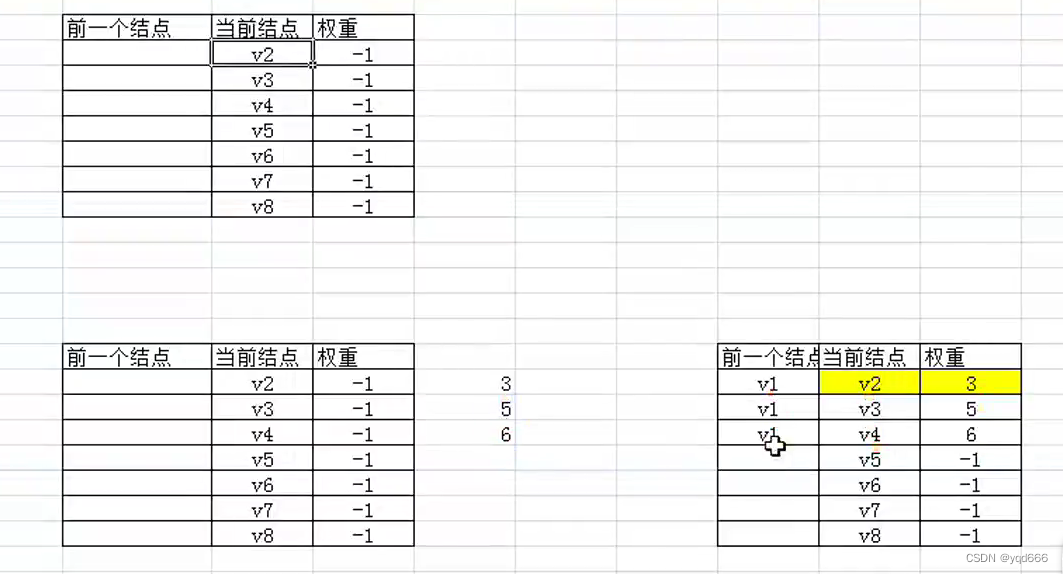
②以V2为顶点

③以V3为顶点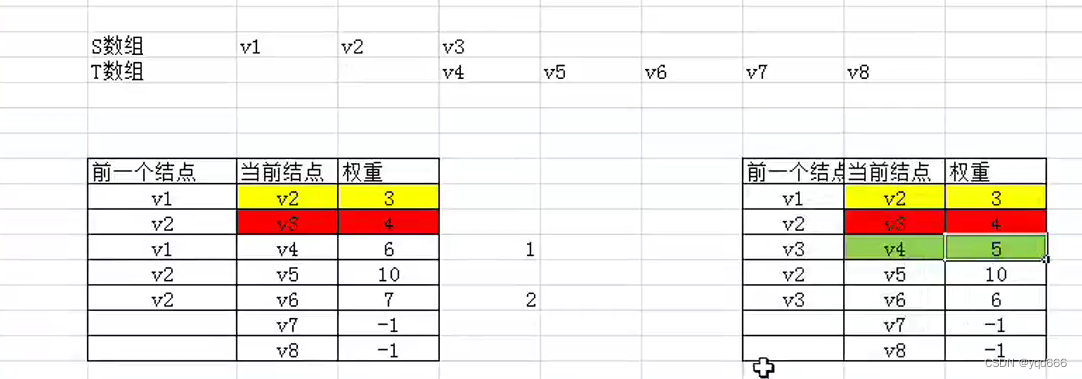
④以V4为顶点

⑤以V6为顶点
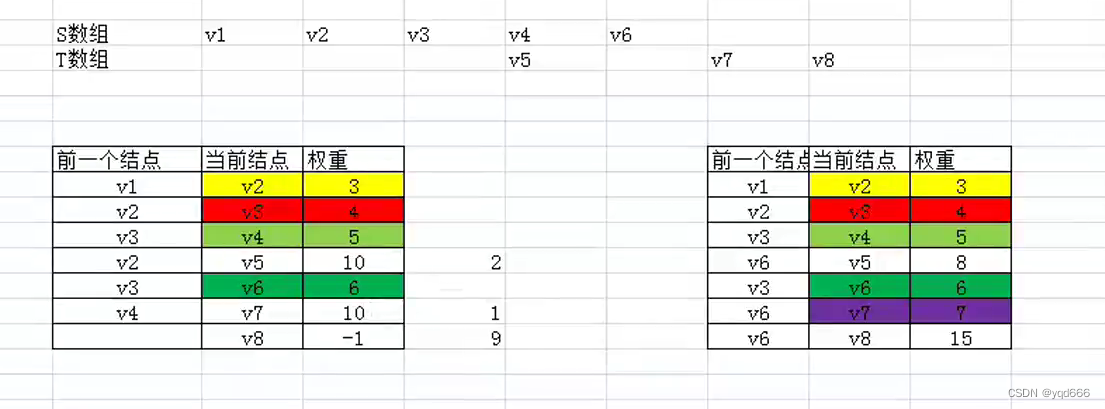
⑥以V7为顶点
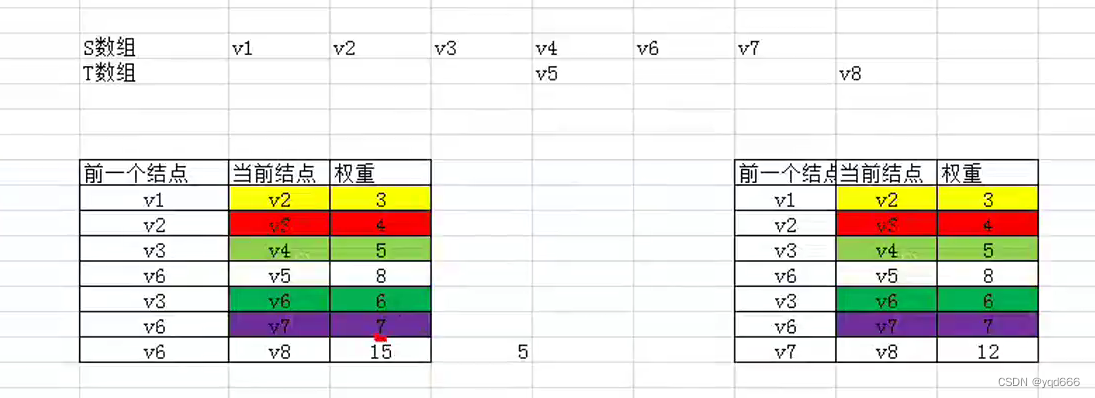
⑦以V5位顶点

⑧最终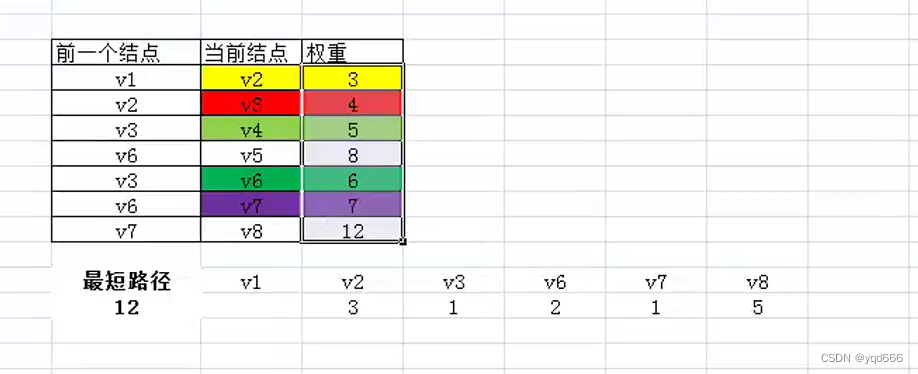
-
相关阅读:
insightface实战:画出嘴巴和眼睛的mask
推荐一个屏幕上鼠标高亮显示的小工具
摸鱼也摸鱼之在线数独自动求解
图解LeetCode——1470. 重新排列数组(难度:简单)
缓存 (模拟两种:数据库提供数据到缓存、外界提供数据到缓存)
java计算机毕业设计校园失物招领管理系统源代码+系统+数据库+lw文档
深入理解计算机系统——第九章 Virtual Memory
Effective Modern C++[实践]->优先使用 scoped enums,而非 unscoped enums
SpringBoot2入门必读(4):Spring boot集成Mybatis(一)
2022网络搭建国赛题中的一道路由与交接题目解析
- 原文地址:https://blog.csdn.net/y516369/article/details/126567192