-
Hash算法 平衡二叉树(调整平衡)
例子:
给定一串数字 10 50 60 1 5 .判断 7 在不在里面
简单的Hash思想
因为最大的数是60,所以定义一个数组长度为int a[] = new int[61]

Hash表(散列表)
散列表的英文就是Hash Table,也就是哈希表,上面的这个例子就是用的是散列表的思想来解决的。
散列表用的是数组支持按照下标随机访问数据的特性,所以散列表就是数组的一种拓展,由数组演化而来。
散列函数(Hash函数)
我们对N取模,N是我们定义的数组的长度即空间的大小,这就是一个散列函数,通过散列函数的计算值我们就可以知道一个数在数组中的存储位置。
现在来看上面例子的另外一种情况:
N:10(数的范围为 1~100000000)
给定五个数 10, 14,52,63,1 判断30在不在
取余:对N取余。a[] = new int[N]
a[10%10] = a[0] = 10
a[14%10] = a[4] = 14
a[52%10] = a[2] = 52
a[63%10] = a[3] = 63
a[1%10] = a[1] = 1
为什么不像上面一样使用0 1来表示是否存在?
因为当我们判断30是否存在的时候,对30取余 也为0
所以a[0]=10 而不是等于30 所以30不存在。
但是仍然存在hash碰撞的问题(hash冲突)
Hash碰撞(hash冲突)
1.探测(开放寻址)

开放寻址如何处理删除
会有一个Delete标记位。假设当index=1的位置被删除了,那么就会把这个位置标记位为已删除。所以当查询的时候就会根据标记位和该位置是否是想要的结果来查询。
2.链表(拉链)

用链表来解决hash冲突
优缺点
优点:相对于上面那种方式,操作更加简单了,发生hash冲突的时候,使用的是链表,更加有利于插入和删除操作。
缺点:链表如果长了,在进行查询的时候,速度慢。
二叉查找树
以根节点为中心,左边的元素都比他小,右边的都比他大。(查询的时候有点类似二分)

问题:极端条件下,二叉查找树可能退化为链表。
平衡二叉树(AVL树)



调整最小不平衡子树
平衡二叉树(AVL)_晓之木初的博客-CSDN博客_avl树全称是什么

LL

右旋:左孩子的左子树加了一个节点,所以就要右旋(即左孩子右上旋)。
*左孩子变成根节点
*左孩子的右子树变为原来根节点的左子树
*原来的根节点变为左孩子的右子树
- // LL,右旋
- public AVLNode rightRotate(AVLNode root) {
- // 右旋,左儿子成为新的根节点
- AVLNode newRoot = root.left;
- // 左儿子的右子树称为根节点的左子树
- root.left = newRoot.right;//这样调整过后 root就变成了最终结果的右子树
- // 根节点成为右儿子的右子树
- newRoot.right = root;
- // 更新高度
- //即最终结果的右子树高度
- root.height = Math.max(getHeight(root.left), getHeight(root.right)) + 1;
- //最终结果左右子树高度最大的一个加一
- newRoot.height = Math.max(getHeight(newRoot.left), root.height) + 1;
- return newRoot;
- }
RR

左旋:右孩子的右子树加了一个节点,所以就要左旋(即右孩子左上旋)。
*右孩子变成根节点
*右孩子的左子树变为原来根节点的右子树
*原来的根节点变为右孩子的左子树
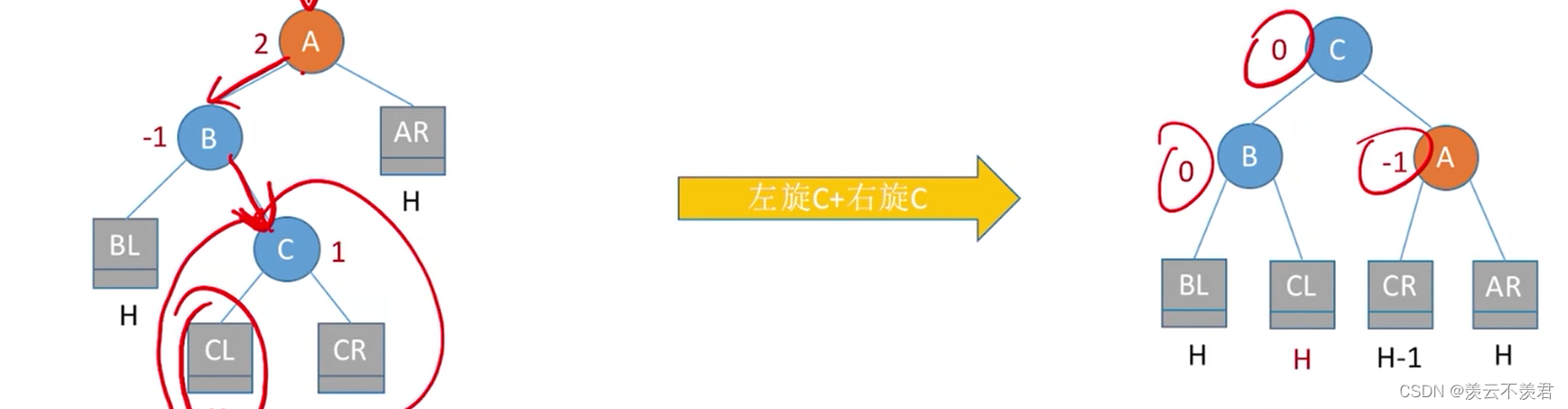
LR
R:那就左旋 L:那就右旋 所以先左旋后右旋

插入到CR位置

也可以是插入到CL位置
RL
R:那就左旋 L:那就右旋 所以先右旋后左旋
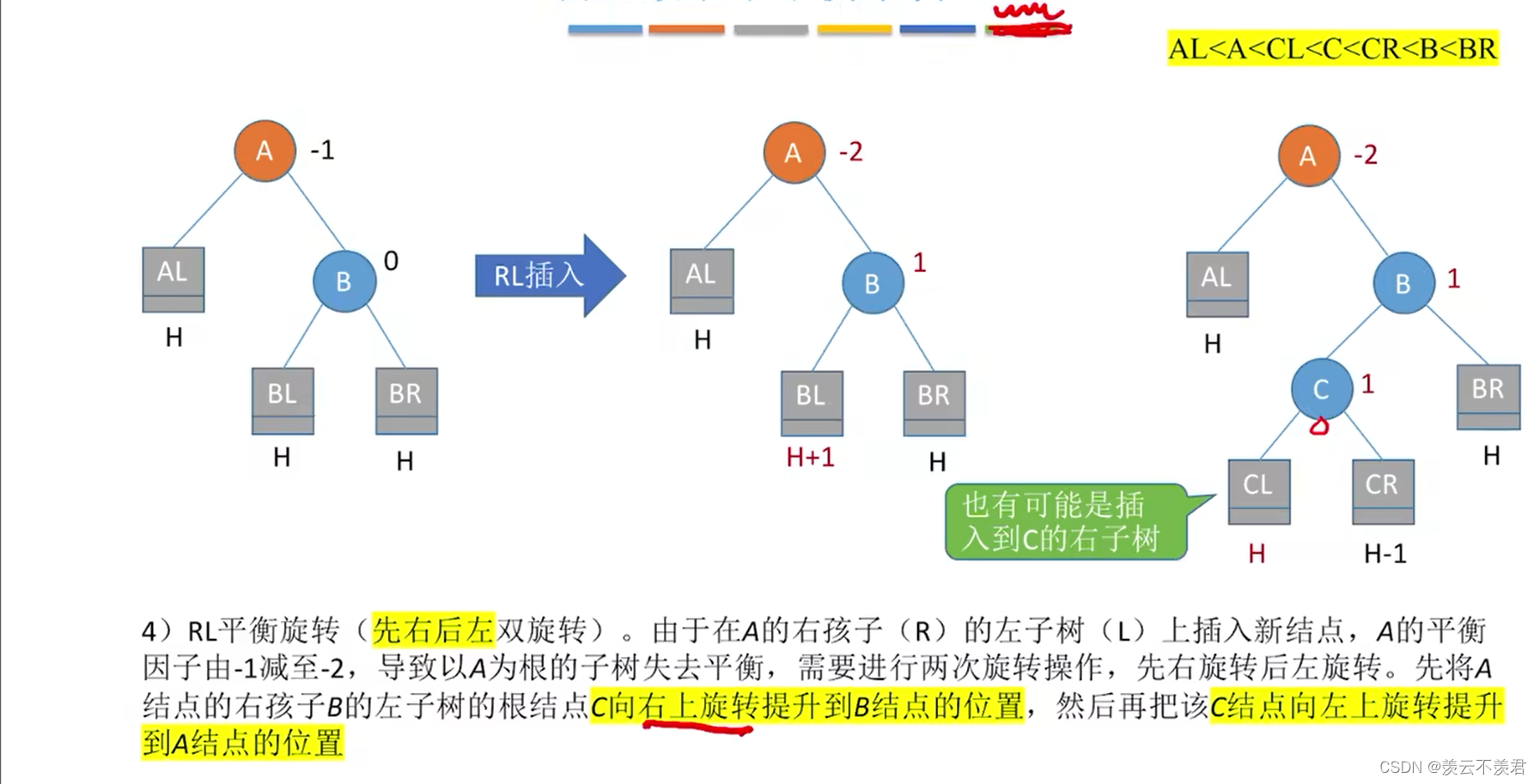
CL处插入

CR处插入

平衡二叉树查找效率

-
相关阅读:
数据驱动!精细化运营!用机器学习做客户生命周期与价值预估!
mysql的存储过程
[思考进阶]02 如何进行认知升级?
C++ Reference: Standard C++ Library reference: C Library: cwchar: swscanf
力扣刷题(6)
计算机视觉五大核心研究任务全解:分类识别、检测分割、人体分析、三维视觉、视频分析
论文研究区域图的制作方法:ArcGIS
《人类简史》笔记二——一场永远的革命
带长度限制的最大子段和,无名一
仿牛客网项目第一章:开发社区首页(详细步骤和思路)
- 原文地址:https://blog.csdn.net/weixin_54401017/article/details/126571596
