神经网络与深度学习-8- 前馈神经网络1 -PyTorch

参考

     《神经网络与深度学习》

---

目录：

1.          神经元
2.          sigmoid 函数
3.         Relu 函数
4.         Swish 函数
5.         GELU 函数
6.        Maxout 函数

---

一  神经元

   把下面一个模型称为一个神经元

   

  

  

 其中 f 为激活函数

其具有以下性质

  1： 连续可导

  2： 激活函数以及其导数要竟可能简单

  3： 激活函数的导数要在一个合适的范围内，不能太大或者太小，影响训练的效率和稳定性

---

二 Sigmoid 型函数

     指的的是一类S型函数,为两端饱和函数，常用的有Logistic 和 Tanh 函数

    备注：

    对于函数f(x),   

    当 ,其,称为左饱和

     当,其,称为右饱和

     同时满足左右饱和时，称为两端饱和

    2.1 sigmoid 激活函数

      

     

      因为 a 范围是0-1,其导数为

       

 2.2 Tanh 激活函数

     

     其导数为

     

   

# -*- coding: utf-8 -*-
"""
Created on Tue Aug 30 17:28:03 2022
@author: chengxf2
"""
# -*- coding: utf-8 -*-
"""
Created on Wed Aug 24 21:09:15 2022
@author: cxf
"""
 
import numpy as np
import matplotlib.pyplot as plt
import torch
 
class active():
    
    TANH = 1
    SIGMOD =2
    RELU = 3
    SOFTPLUS = 4
    SWISH = 5
    GELU = 6
    MAXOUT = 7
    SOFTMAX = 8
 
    
 
'''
激活函数
args
   z: 激活单元输入
return 
   a : 神经元输出
'''
def  f(z, act):
    
    if act is active.TANH:
        a = torch.tanh(z)
        tip ="tanh"
    
    elif act is active.SIGMOD:
         a = torch.sigmoid(z)
         tip = "Sigmoid"
    elif act is active.RELU:
         a = torch.relu(z)
         tip ="Relu"
    elif act is active.SOFTMAX:
         a = 1+torch.exp(z)
         a = torch.log(a)
         tip = "SoftPlus"
    elif  act is active.SWISH:
         beta = 0.5
         a = z*torch.sigmoid(beta*z)
         tip ="Swish"
    elif act is active.GELU:
          tip ="GELU"
          m = np.sqrt(2/np.pi)*(z+0.044715*np.power(z,3))
          a = 0.5*z*(1.0+torch.tanh(m))
         
   
          tip ="GELU"
    return a ,tip
        
    
    
'''
绘画
args
   act: 激活函数类型
'''
def Draw(act):
    z = np.linspace(-10,10,100)
    
    zTensor = torch.FloatTensor(z)
    
    a,tip = f(zTensor,act)
    
    #print(b)
    
    plt.plot(z, a.numpy(), color='g',marker=".",linestyle="-")
    plt.title(tip)
    plt.xlabel("z")
    plt.ylabel("a")
    
    plt.grid()
    plt.show()
    
Draw(active.GELU)

---

二  Hard-Logistic 函数和  Hard-Tanh 函数

       Logistic 函数 和 Hard-Tanh 都是非线性函数,在SISO算法里面有讲过

其计算时间是线性函数的50倍左右。

    这边给出来其算法简化的方向

    2.1 Logistic 函数 hard-Decision

    

              

                 

                 

               

   2.2 tanh 函数 hard-Decision

                    

                             

                     

 2.3 ReLu （Rectfoed Linear Unit   修正线性单元）

        

                           。

优点

        为左饱和函数，x>0导数为1 ，一定程度上缓解了梯度消失问题 

缺点：

     输出是非零中心化的，相当于给后面一层引入了偏置偏移，会影响梯度下降的效率

ReLu 在训练时候容易死亡

   

  带泄露的ReLu 

    

             

   r 是特别小的常数，比如0.01 ,也可以写作

   

   当神经元非激活的时候，能有一个非零的梯度可以更新参数，避免了不能被激活。

  带参数的ReLu

   对第i个神经元

  

           

   2.4 ELU 函数（Exponential Linear Unit）

      

                         

  2.5 softPlus 函数

     

2.6 Swish 函数

      Swish 是一种自门控（self-Gated）激活函数

      

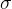      : 为Logistic 函数

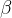      为可学习的参数或一个固定超参数

 

2.7 GELU 函数（Gaussian Error Linear Unit 高斯误差线性单元）

     通过门控制来调整其输出值的激活函数，和Swish 函数相似

     

      的累积分布函数，其中为超参数

   

2.8 Maxout 单元

    也是一种线性分段函数，输入是上一个层神经元的原始输出

  是一个向量