-
机器学习中的各种损失函数(L1,L2,smoothL1,交叉熵 )
机器学习中的各种损失函数:
二分类交叉熵损失函数Binary Cross Entropy Loss
平方误差损失(L2 loss)
每个训练示例的平方误差损失,也称为“L2损失”,是实际值与预测值之差的平方。
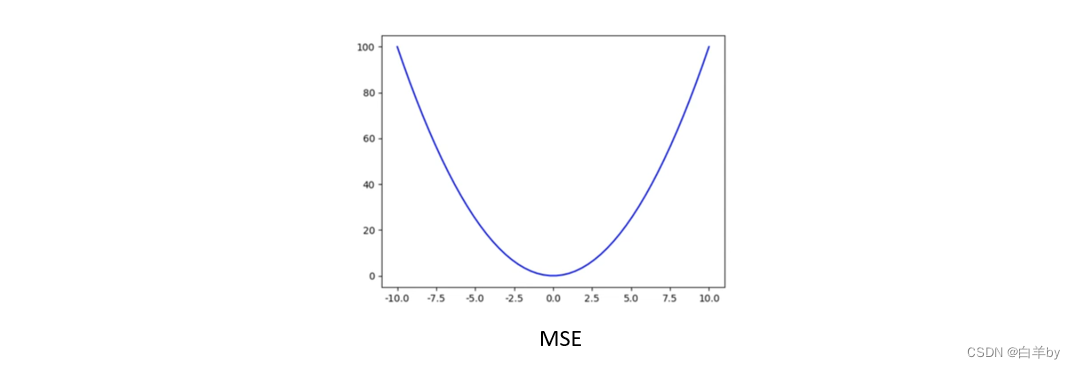
 相应的代价函数是,这些平方误差的均值(MSE)
相应的代价函数是,这些平方误差的均值(MSE)
MSE损失函数。它是一个正二次函数(形式为ax^2 + bx + c,其中a > 0)二次函数只有全局最小值,因此,始终保证梯度下降将收敛(如果它完全收敛)到全局最小值。
进行梯度下降时,MSE的偏导数为

绝对误差损失(L1 loss)
每个训练示例的绝对误差是预测值和实际值之间的距离,与符号无关。绝对误差也称为L1损失:

基于L1的loss代价函数称为绝对误差的平均值(MAE)。

MAE损失函数是绝对值函数,只有全局最小值,因此,始终保证梯度下降将收敛(如果它完全收敛)到全局最小值。

进行梯度下降时,MAE的偏导数为

Smooth L1 Loss(Huber)
SmoothL1Loss为平方误差的修改版,为分段函数,对离散点不敏感,具体的公式如下:

L1、L2和SmoothL1损失函数可视化结果如图

合页损失Hinge loss
Hinge损失主要与类标签为-1和1的SVM分类器一起使用。
Hinge Loss不仅会惩罚错误的预测,还会惩罚不自信的正确预测。
Hinge Loss简化了SVM的数学运算,同时最大化了损失(与Log-Loss相比)。当我们想要做出实时决策而不过于关注准确性时使用它。
输入和输出对(x, y)的Hinge loss为:

Hinge loss的可视化结果为

二分类交叉熵损失函数Binary Cross Entropy Loss
给出了离散版、连续版两个函数,主要区别是离散用求和,连续用积分。
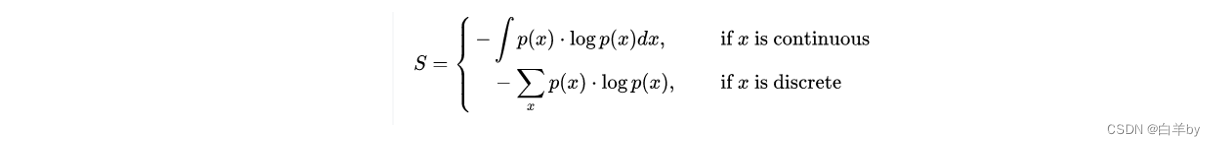
负号用于使总量为正。概率分布的熵值越大,表示分布的不确定性越大。相反,熵越小表示模型预测的越确定。
二分类化简之后的结果如下:

多分类交叉熵损失函数Categorical Cross Entropy Loss:
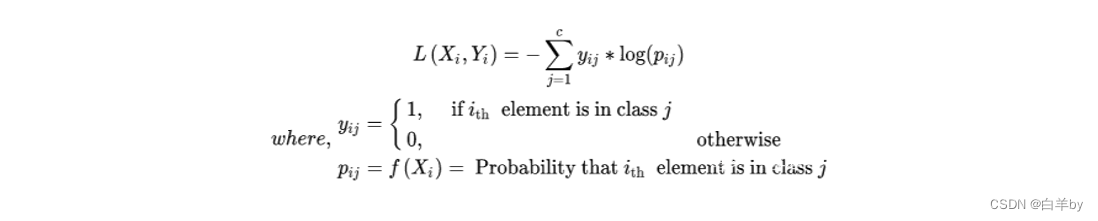
-
相关阅读:
SimpleCG程序交互操作
Unity角色同时播放两个音效(走路音效+说话音效)
什么是运营商网关取号
下载无水印抖音视频
AVS感知无损压缩标准概述——视觉无损质量等级视频浅压缩
数据结构-栈结构扩展应用
Spring:Bean生命周期
UML中类之间的六种主要关系
【数据可视化】数据可视化入门前的了解
王道3.1 顺序栈以及链式栈
- 原文地址:https://blog.csdn.net/weixin_45848575/article/details/126566493