数据结构-Dijkstra最短路径算法

1、图结构
共V0~V6七个顶点

2、创建三个辅助数组
S:记录目标顶点到其他顶点的最短路径是否求得，初始化时，s[index]记为1，其余记为0;
P:记录目标顶点到其他顶点的最短路径的前驱节点，初始化时，p[index]记为-1，其余记为index;
D:记录目标顶点到其他顶点的最短路径长度，初始化为初始顶点到其余各顶点的权值，d[index]=0;

3、程序流程
（1）不妨选择V0顶点作为初始顶点，计算各顶点到V0的路径长度

（2）选择到V0顶点路径最短的V1顶点，作为中转顶点

计算剩余的V2~V6顶点到V1的直连距离，与V0的直连距离进行比较，看经过V1中转后的路径是否更短，若更短则替换。

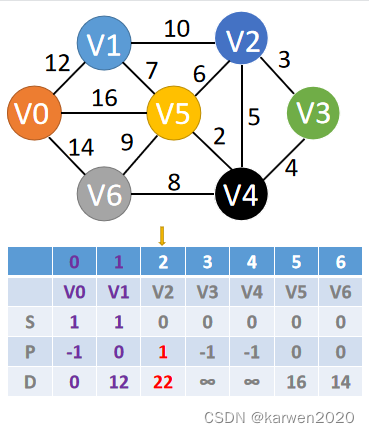
（3）选择D数组中最短的距离D[6]

计算经过V6顶点的V2~V5的距离

更改最短距离和经过的顶点

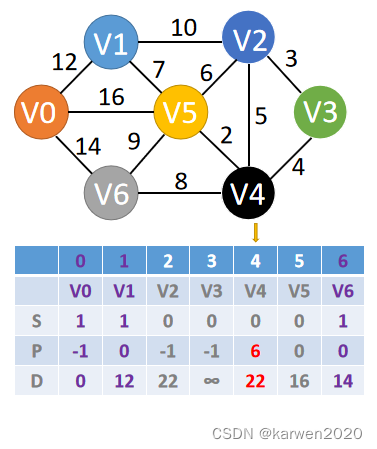
（4）选择经过点V5

计算V0顶点经过V5到达V2、V3、V4顶点的距离

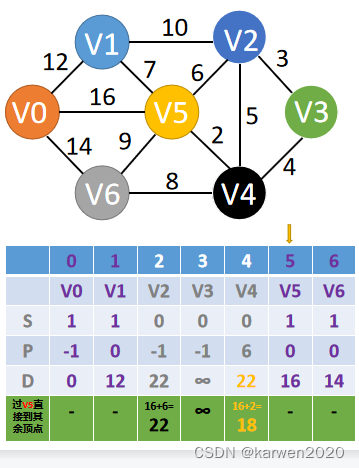
选择最短距离V4

更改V4的前一顶点

（5）选择经过顶点V4，并计算到剩余V2、V3顶点的距离

更改到V3的最短距离

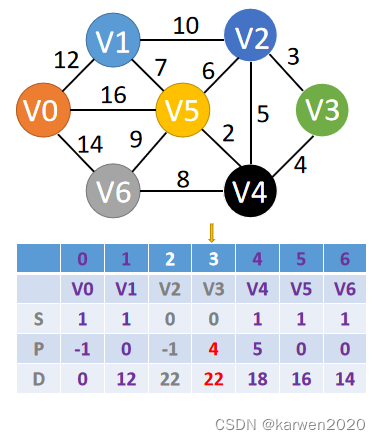
按前后顺序，选择V2为经过点

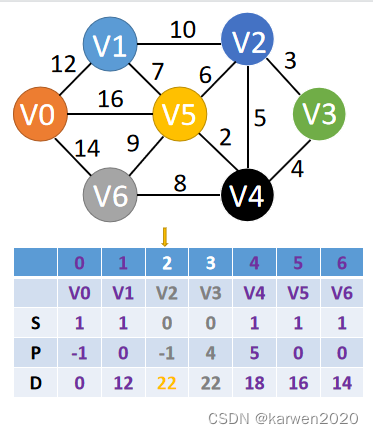
更改P、S数组

（6）选择V2作为经过点，计算至剩余节点V3的距离

（7）选择最后一个顶点

至此V0至各顶点的最短路径全部计算完
在这里插入图片描述

P=[-1,0,1,4,5,0,0];
D=[0,12,22,22,18,16,14];
代表的含义为：
V0~V0的距离为：0，经过的点为：V0->V0
V0~V1的距离为：12，经过的点为：V0->V1
V0~V2的距离为：22，经过的点为：V0->V1->V2
V0~V3的距离为：22，经过的点为：V0->V5->V4->V3
V0~V4的距离为：18，经过的点为：V0->V5->V4
V0~V5的距离为：16，经过的点为：V0->V0
V0~V6的距离为：14，经过的点为：V0->V0
1
2
3
4
5
6
7
8
9
10

4、程序代码

#include 
#include 
#define MAX 65535
typedef struct Graph{
    char* vertexes;
    int** arcs;
    int vertexNum;
    int arcNum;
}Graph;

Graph* initGraph(int vertexNum){
    Graph* G=(Graph*)malloc(sizeof (Graph));
    G->vertexes=(char*)malloc(sizeof(char)*vertexNum);
    G->arcs=(int**)malloc(sizeof(int*)*vertexNum);
    for(int i=0;i<vertexNum;i++){
        G->arcs[i]=(int*)malloc(sizeof (int)*vertexNum);
    }
    G->vertexNum=vertexNum;
    G->arcNum=0;
    return G;
}
void createGraph(Graph* G,char* vertexes,int *arcs){
    for(int i=0;i<G->vertexNum;i++){
        G->vertexes[i]=vertexes[i];
        for(int j=0;j<G->vertexNum;j++){
            G->arcs[i][j]=*(arcs+i*G->vertexNum+j);
            if(G->arcs[i][j] != 0 && G ->arcs[i][j] != MAX){
                G->arcNum++;
            }
        }
    }
    G->arcNum>>1;
}
void DFS(struct Graph* G,int* visited,int index){
    printf("%c\t",G->vertexes[index]);
    visited[index] = 1;
    for(int i = 0;i < G->vertexNum;i++){
        if(G -> arcs[index][i] > 0 && G->arcs[index][i] != MAX && !visited[i] ){
            DFS(G,visited,i);
        }
    }
}
int getMin(int *d,int *s,Graph* G){
    int min = MAX;
    int index;
    for(int i = 0;i <G ->vertexNum;i++){
         if(!s[i] && i != index && d[i] < min){
            min = d[i];
            index = i;
        }
    }
    return index;
}
void dijkstra(Graph* G,int index){
    int min = MAX;
    int minIndex;
    int *s = (int*)malloc(sizeof (int)*G->vertexNum);
    int *p = (int*)malloc(sizeof (int)*G->vertexNum);
    int *d = (int*)malloc(sizeof (int)*G->vertexNum);
    /*辅助数组初始化*/
    for(int i = 0;i < G->vertexNum;i++){
        if(i == index){
            s[i] = 1;
        }else{
            s[i] = 0;
        }
    }
    for(int i = 0;i < G->vertexNum;i++){
        if( G->arcs[index][i] > 0 && G->arcs[index][i] != MAX){
            p[i] = index;
        }else{
            p[i] = -1;
        }
    }
    for(int i = 0;i < G->vertexNum;i++){
        d[i] = G->arcs[index][i];
    }
    /**dijkstra核心代码**/
    for(int i = 0; i < G->vertexNum - 1;i++){
        minIndex = getMin(d,s,G);
        s[minIndex] = 1;
        for(int j = 0;j < G->vertexNum;j++){
            if(!s[j] && d[minIndex] + G->arcs[minIndex][j] < d[j]){
                d[j] = d[minIndex] + G->arcs[minIndex][j];
                p[j] = minIndex;
            }
        }
    }
    for(int i = 0; i < G->vertexNum;i++){
        printf("%d %d %d\n",s[i],p[i],d[i]);
    }
}

int main(){
    Graph* G = initGraph(7);
    int *visited = (int*)malloc(sizeof (int)*G->vertexNum);
    for(int i = 0;i < G -> vertexNum;i++){
        visited[i] = 0;
    }
    int arcs[7][7] = {
            0,12,MAX,MAX,MAX,16,14,
            12,0,10,MAX,MAX,7,MAX,
            MAX,10,0,3,MAX,6,MAX,
            MAX,MAX,3,0,4,MAX,MAX,
            MAX,MAX,MAX,4,0,2,8,
            16,7,6,MAX,2,0,9,
            14,MAX,MAX,MAX,8,9,0
    };
    createGraph(G,"0123456",(int*)arcs);
    DFS(G,visited,0);
    printf("\n");
    dijkstra(G,0);

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116

5、运行结果

0       1       2       3       4       5       6
1 -1 0
1 0 12
1 1 22
1 4 22
1 5 18
1 0 16
1 0 14
1
2
3
4
5
6
7
8