数据结构——树

想要查询一个数组

需要遍历数组，时间复杂度为O(n)

如何降低时间复杂度呢?

我们知道有序数组可以使用折半查找法，其时间复杂度为O(logn)，但是一个数组变成有序数组最低也需要O(nlogn)，这样并不能降低时间复杂度。

简化数组查询的时间复杂度——这就是树的产生的背景

树（有序二叉树）——时间复杂度是O(logn)

把数组{5，3，7，2，4，6，8}按如图的形式存储，这就是树

树的基本概念

树按孩子划分一般分为二叉树和多叉树

叶子节点：没有孩子的节点

节点的权：即value值

二叉树

每个节点最多有两个子节点

二叉树的种类

完全二叉树：数据从上到下，再从左到右进行排列，度为1的节点只能有一个
满二叉树：叶子节点都在一层上，且最后一层节点数位2 ^ n-1（最后一层是满的）。满二叉树一定是完全二叉树，发过来不一定
有序二叉树
平衡二叉树
红黑树
哈夫曼树

二叉树的遍历

深度优先遍历（根据父节点输出的顺序区分）

先序遍历：先输出父节点，再输出左节点，再输出右节点
中序遍历：先输出左节点，再输出父节点，再输出右节点
后序遍历：先输出左节点，再输出右节点，再输出父节点

看父节点的输出顺序就能看出是哪一种遍历方式，父节点在第一位，可能是先序或者中序（看树的结构），父节点在最后一位，可能是后序或者中序，父节点在中间，只能是中序遍历

//先序遍历（根左右）
    public void  beforeOrder(TreeNode node){
        if (node == null){
            return;
        }
        System.out.println("" + node.getValue()+ "");
        beforeOrder(node.getLeftTreeNode());
        beforeOrder(node.getRightTreeNode());
    }
    //中序遍历（左根右）
    public void  inOrder(TreeNode node){
        if (node == null){
            return;
        }
        inOrder(node.getLeftTreeNode());
        System.out.println("" + node.getValue()+ "");
        inOrder(node.getRightTreeNode());
    }
    //后序遍历(左右根)
    public void  afterOrder(TreeNode node){
        if (node == null){
            return;
        }
        afterOrder(node.getLeftTreeNode());
        afterOrder(node.getRightTreeNode());
        System.out.println("" + node.getValue()+ "");
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

中序遍历非递归版本

//中序遍历（非递归版本）
public ArrayList<Integer> inorderTraversal(TreeNode root) {
        TreeNode cur = root;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        ArrayList<Integer> ans = new ArrayList<Integer>(20);
        while (cur != null || !stack.isEmpty()) {
            // 相当于一个开关
            if (cur != null) {
                stack.push(cur);
                cur = cur.getLeftTreeNode();
            }
            else {
                cur = stack.pop();
                ans.add(cur.getValue());
                if (cur.getRightTreeNode() == null) {
                    cur = null;
                }
                else {
                    cur = cur.getRightTreeNode();
                    stack.push(cur);
                    cur = cur.getLeftTreeNode();
                }
            }
        }
        return ans;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

广度优先遍历（层次遍历）

利用辅助队列（先进先出）实现广度优先遍历——>队列的底层一定是一个链表（数组存在空间不够的情况，避免空间不足）

当结点从队列中pop出来打印的时候，把结点的左子树和右子树根结点push进入队列，这样能够保证同一个深度的结点在队列中连续排布

我们要一层一层的遍历？那么如何在输出5后，去获取其左右孩子，并循环？————我们可以借助队列，队列先入根节点（然后判断是否有左右孩子），有的话把左右孩子存入队列（先进先出），把根节点给弹出（循环整个过程）
//广度优先遍历（层次遍历）
public void levelOrder(){
 LinkedList<TreeNode> queue= new LinkedList<>();
 queue.add(root);
 while (!queue.isEmpty()){
     root = queue.pop();
     if (root.getLeftTreeNode() != null){
         queue.add(root.getLeftTreeNode());
     }
     if ( root.getRightTreeNode() != null){
         queue.add(root.getRightTreeNode());
     }
     System.out.print(root.getValue() + " ");
 }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
package com.qcby.datastructure.tree;

public class Test {
 public static void main(String[] args) {
     BinaryTree binaryTree =new BinaryTree();
     binaryTree.insert(5);
     binaryTree.insert(7);
     binaryTree.insert(4);
     binaryTree.insert(2);
     binaryTree.insert(0);
     binaryTree.insert(3);
     binaryTree.levelOrder();
 }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

二叉树的查找

public TreeNode select(int value){
    LinkedList<TreeNode> queue= new LinkedList<>();
    queue.add(root);
    while (root.getValue() != value && !queue.isEmpty()){
        root = queue.pop();
        if (root.getLeftTreeNode() != null){
            queue.add(root.getLeftTreeNode());
        }
        if ( root.getRightTreeNode() != null){
            queue.add(root.getRightTreeNode());
        }
    }
    return root;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

有序二叉树的构建

传统方法

package com.qcby.datastructure.tree;

import javafx.scene.transform.Rotate;

public class BinaryTree {
    public TreeNote root;//代表了一整个树，而不是根节点
    public void insert(Integer value){
    //创建一个节点
        TreeNote newNode = new TreeNote(value);
        if (root==null){
            root=newNode;
            return;
        }
        //定义游标来遍历二叉树
        TreeNote currentNote = root;
        //定义一个游标来记录currentNode的前一个地址
        TreeNote preNode = null;
        while (true) {
            preNode = currentNote;
            //判断currentNode指向的值和value进行对比
            if (newNode.getValue() > currentNote.getValue()) {
                //游标需要往右走
                currentNote = currentNote.getRightTreeNode();
                //右子树为空
                if (currentNote == null) {
                    preNode.setRightTreeNode(newNode);
                    return;
                }
            }
            else {
                //游标需要往左走
                currentNote = currentNote.getLeftTreeNote();
                //左子树为空
                if (currentNote == null) {
                    preNode.setLeftTreeNote(newNode);
                    return;
                }
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

递归方法

先找递归表达式

再找递归出口

 //采用递归的方式，来插入数据（有序二叉树）
    public void insertDiGui(TreeNode node, Integer value){
        //新建节点
        TreeNode newNode = new TreeNode(value);
        if (root ==null){
            root = newNode;
            return;
        }
        if (node.getValue() > value){
            //递归出口。插入去完成的时候
            if (node.getLeftTreeNode() == null){
                node.setLeftTreeNote(newNode);
                return;
            }
            insertDiGui(node.getLeftTreeNode(), value);
        }else {
            if (node.getRightTreeNode() == null){
                node.setRightTreeNode(newNode);
                return;
            }
            insertDiGui(node.getRightTreeNode(), value);
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

测试

public static void main(String[] args) {
    TreeNode node =new TreeNode(5);
    binaryTree.insertDiGui(node,7);
    binaryTree.insertDiGui(node,4);
    binaryTree.insertDiGui(node,2);
    System.out.println(node);
}
1
2
3
4
5
6
7

有序二叉树的删除

跳过要删除的节点（没有对象指向该节点），jvm回收机制就会回收该节点的内存空间

删除节点后，保证还是有序二叉树

删除叶子节点

删除节点只有一个子树

删除节点有两个子树

/**
     *递归查找节点
     * @param node
     * @param value
     * @return
     */
    public TreeNode searchTargetNode(TreeNode node,int value){
        //判断不是空树
        if (root == null) {
            return null;
        }
        if (value == node.getValue()){
            return node;
        }else if (value <node.getValue()){
            if (node.getLeftTreeNode()==null){
                return null;
            }
            return searchTargetNode(node.getLeftTreeNode(),value);
        }else {
            if (node.getRightTreeNode()==null){
                return null;
            }
            return searchTargetNode(node.getRightTreeNode(),value);
        }
    }

    //查询节点的父节点
    public TreeNode searchParentNode(TreeNode node,int value){
        //判断不是空树
        if (root == null) {
            return null;
        }
        //判断当前节点是不是我们删除节点的父节点
        if((node.getLeftTreeNode() !=null && node.getRightTreeNode().getValue()== value) ||
                (node.getRightTreeNode() !=null && node.getRightTreeNode().getValue() ==value)){
            return node;
        }else {
            if(node.getLeftTreeNode() !=null && value<node.getValue()){
                return searchParentNode(node.getLeftTreeNode(),value);
            }else if(node.getRightTreeNode() !=null && value>node.getValue()){
                return searchParentNode(node.getRightTreeNode(),value);
            }else {
                return null;
            }
        }
    }
    /**
     * 找打右子树的最小值
     * @param node
     * @return
     */
    public int deleteRightMin(TreeNode node){
        //定义指针
        TreeNode target = node;
        while (target.getLeftTreeNode() !=null){
            target = target.getLeftTreeNode();
        }
        deleteNode(root,target.getValue());
        return target.getValue();
    }
    //删除节点(删除后还是有序二叉树)
    public void deleteNode(TreeNode node,int value){
        if (node == null){
            System.out.println("这是一个空树");
            return;
        }
        //找到要删除的节点
        TreeNode targetNode = searchTargetNode(node, value);
        //判断有没有这个节点
        if (targetNode ==null){
            System.out.println("没有这个节点");
            return;
        }
        //表示该树只有一个节点
        if (node.getLeftTreeNode() == null && node.getRightTreeNode() == null){
            root = null;
            return;
        }
        //找到这个节点的父节点
        TreeNode parentNode = searchParentNode(node, value);
        //这是一个叶子节点
        if (targetNode.getLeftTreeNode() == null && targetNode.getRightTreeNode() == null){
            //确认targetNode是parentNode的左子树还是右子树
            if (parentNode.getLeftTreeNode() !=null && parentNode.getLeftTreeNode().getValue() == value){
                parentNode.setLeftTreeNote(null);
            }else if (targetNode.getRightTreeNode() !=null && parentNode.getRightTreeNode().getValue() ==value){
                parentNode.setRightTreeNode(null);
            }

        }
        //目标节点左右子树都不空，表示有两个子树的节点
        else if (targetNode.getLeftTreeNode() !=null && targetNode.getRightTreeNode() != null){
            //找到右子树的最小值
            int minValue =  deleteRightMin(targetNode.getRightTreeNode());
            targetNode.setValue(minValue);
        }
        //只有一个子树的情况
        else {
            //判断 targetNode是有左子树还是有右子树
            if(targetNode.getLeftTreeNode() !=null){ //有左子树
                //判断targetNode 是parentNode的左子树还是右子树
                if(parentNode.getLeftTreeNode().getValue() == value){  //targetNode 是parentNode的左子树
                    parentNode.setLeftTreeNote(targetNode.getLeftTreeNode());
                }else { //targetNode 是parentNode的右子树
                    parentNode.setRightTreeNode(targetNode.getLeftTreeNode());
                }
            }else {//有右子树
                //判断targetNode 是parentNode的左子树还是右子树
                if(parentNode.getLeftTreeNode().getValue() == value){  //targetNode 是parentNode的左子树
                    parentNode.setLeftTreeNote(targetNode.getRightTreeNode());
                }else { //targetNode 是parentNode的右子树
                    parentNode.setRightTreeNode(targetNode.getRightTreeNode());
                }
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116

平衡二叉树

平衡二叉树的背景

传统数组的查询是依靠遍历（时间复杂度为O(n)），有序数组的查询的时间复杂度是（O(logn)）——折半查找法。但是无序数据变成有序数组的最小时间复杂度为O(nlogn)。

有人提出了哈希算法来减少时间复杂度，

**哈希算法：**通过一个公式计算出的值作为索引把值存入哈希表中，理想情况下（没有哈希碰撞）的情况下，用哈希算法的查询时间复杂度为O(1)。

哈希碰撞：两个或多个值通过哈希算法得到同一个值——哈希碰撞

如何解决哈希碰撞的问题：————拉链法

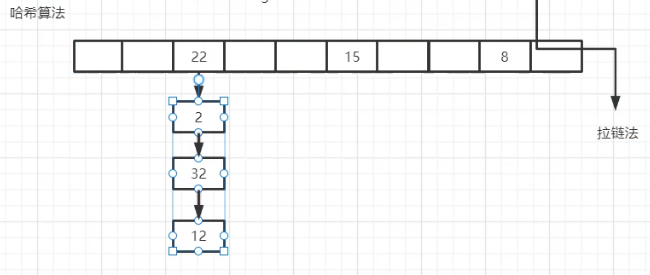
使用链表来存放哈希碰撞的数据

拉链法的弊端———随着碰撞的数据越来越多，拉链法在链表上的查询的时间复杂度为o(n)

如何降低链表的查询时间复杂度？

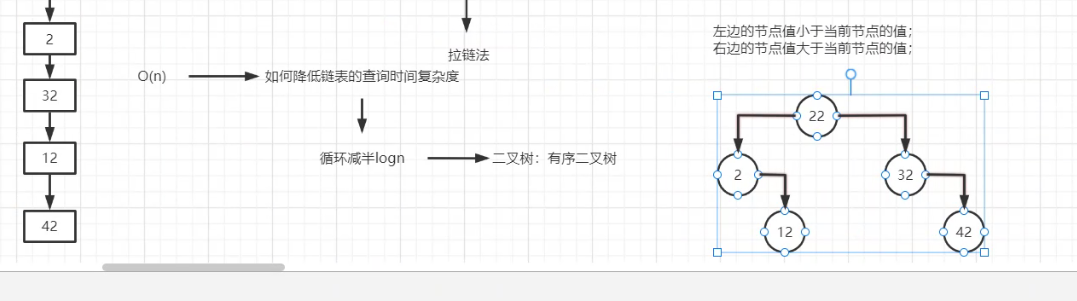
通过引进树的概念（把链表构建成有序二叉树）

有序二叉树理论上的查询的时间复杂度为O(logn)

那么有序二叉树存在的问题呢？试想一个极端情况，如下图，这个有序二叉树查询的时间复杂度为O(n)

理论上有序二叉树查询的时间复杂度是一个logn级别的，实际上是在logn到n之间(不稳定)

如何解决有序二叉树不稳定的问题？

引入平衡二叉树

平衡二叉树的概念

1.平衡二叉树是一个有序二叉树（左边的节点值小于当前节点值小于右边节点值）

2.左右两颗子树的高度差的绝对值小于等于1

平衡二叉树的旋转

在插入新的节点后，可能会导致平衡二叉树不再”平衡“，我们通过旋转来使二叉树重新达到平衡

每次跳转只走两步来判断是什么型

LL型旋转

先找新插入的节点（造成不平衡的节点）

找到不平衡节点（离造成不平衡节点最近的）

将A节点的左孩子提升为新的跟节点
将跟节点A变为新跟节点的右子树
剩余各个子树按大小关系排列

举例1

举例2

造成不平衡的节点1

不平衡节点 4

RR型旋转

先找新插入的节点（造成不平衡的节点）

找到不平衡节点（离造成不平衡节点最近的）

将A节点的右子树B升为子树的根节点点
节点A降为B的左子树
其与子树按大小关系进行排列

举例

LR型旋转

先找新插入的节点（造成不平衡的节点）

找到不平衡节点（离造成不平衡节点最近的）

例子

不平衡点：5

造成不平衡的点：3

RL型旋转

先找新插入的节点（造成不平衡的节点）

找到不平衡节点（离造成不平衡节点最近的）

例子

红黑树（最优二叉树）

二三四树

二三四树查找的实际时间复杂度会小于平衡二叉树（O(logn)）

二三四树所有叶子节点保存着相同的深度

二三四树转换红黑树

2节点的只能变成一个黑节点

3节点变成一个黑节点连接着一个子红节点

4节点变成一个黑色节点连接着两个子红节点

红黑树也是一个有序二叉树

红黑树的特点

由2-3-4树过渡而来

每个节点不是黑色就是红色
根节点永远都是黑色——转换的时候是黑色在上
红黑树有叶子节点，每个叶子节点都是null
如果一个节点是红色的，那么他的子节点一定是黑色的（由二三四树转换红黑树可知，红色节点是二三四树的结束，而黑色节点是开始）
从根节点到任意一个叶子节点上的黑色节点的数目相同（二三四树所有叶子节点保存着相同的深度）
在红黑树上没有一条路径比其他路径长过2倍
假设极端情况，红黑树路径最长的就是红黑相间的，但是红黑树任意路径的黑色节点数目相同，最长路径红色节点最多=黑色节点的数量，所以在红黑树上没有一条路径比其他路径长过2倍

多叉树

B树

一个节点上可以分出多个（2个以上）的分支

B树是多叉树（有序），如2-3-4树就是B树（3阶b树，最多三个分支）

一个节点最多能有多少分支（就是几阶b树）——B树中所有结点的孩子结点个数的最大值即为阶吧

m阶b树，每个节点上最多存储m-1个值，如4阶b树每个节点上最多存储3个值

B树的存储格式是以key—value形式存储的，按key值排序

导线中传递是电压而不是电流（电压的变化小，稳定）

一个导线一次只能传递一个电压信号，为了解决这个问题，把多个导线并联形成总线，可以一个时刻传递多个电压信号，总线的根数表示了是几位的操作系统

B+树

数据库底层数据结构采用B+树

B+树非叶子节点仅具有索引功能，非叶子节点上只能存储key值，不能存储value值

B+树非叶子节点上存储数据越多，树的高度越低

B+树的叶子节点会构成一个有序链表，有利于区间查询

对于一个查询语句

select * from user where id = ?
1

key：主键id

value：数据

哈夫曼树和哈夫曼编码

哈夫曼树和哈夫曼编码的背景

如：I LOVE YOU如何变成二进制信息就行存储呢？

是通过编码格式表（以ASCII码为例）

ASCII码是针对于英文的编码格式，一个字符占8bit

I LOVE YOU有10个字符（中间两个空格）

采用定长编码的方式，那么就需要80个bit

定长编码：无论数据多大，都存储为固定大小，小的话则前补，大的话就裁剪

定长编码：能够方便的进行截取数据

数据压缩

网络并不稳定，把数据进行压缩，提高数据的传输速度

如何进行数据压缩

把定长的编码变成变长的编码，就可以减少空间

如何设计一个变长的编码规则

我们可以把字符的出现次数做一个统计，字符出现次数越多，编码后占用的bit越少，这样就可以有效进行数据压缩（把出现次数多的字符，减少了占用的bit）

如下图，空格和o出现的最多，编码后他们代表0和1 u只出现了一次，编码后代表的是110

采用变长编码可以有效的数据压缩，但是对应的在数据解析（解压、翻译）对的时候，无码正确识别编码，数据的翻译会出现歧义

如何在采用变长编码进行数据压缩的同时，也确保数据翻译的正确性呢？————哈夫曼编码————哈夫曼树

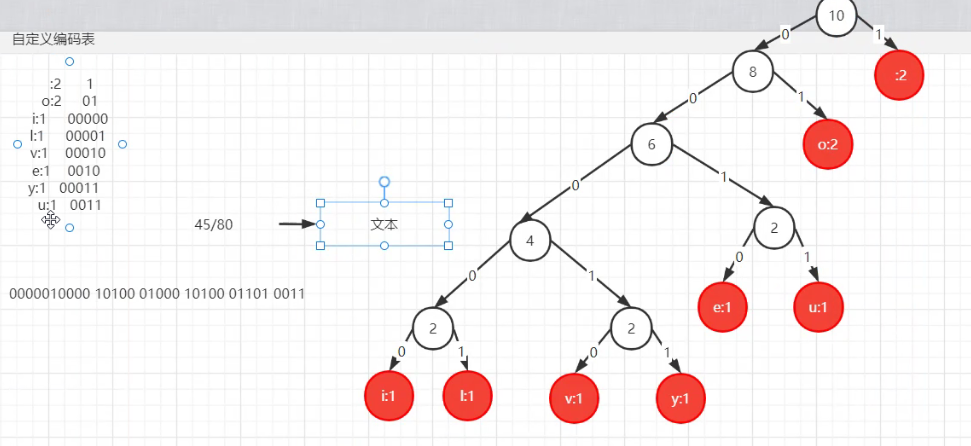
可以看出哈夫曼编码的前缀是不重复的，哈夫曼编码的平均压缩效率在60%左右，但是不会出现翻译歧义的现象发生。

哈夫曼树

基本概念

路径和路径长度：根节点到该节点中间的路径数量，如根节点到13的路径长度为2

节点的权：节点的value值（一般为数出现的次数）

带权路径长度：路径长度 * 节点的权

树的带权路径长度（WPL）：每条路径上带权路径长度之和

树的带权路径长度（WPL）最小的就是哈夫曼树

哈夫曼树所有节点的权全在叶子节点上

哈夫曼树不唯一，但是一定是最小的WPL

构建哈夫曼树

给定一个数组

1.从小到大进行排序

2.把数组的数放入一个集合，取出集合中最小的数（一个或者两个），构成的新节点也进入集合，但是不是实际的节点。哈夫曼树所有节点的权全在叶子节点上.

3.重复第二步，直到所有节点构成一个树

相关阅读:
Java编程语言是什么传递，即值传递和引用传递的区别
 C++11 - 4 -万能引用
 【golang】sync包once 只执行一次代码
 golang八股文整理（持续搬运）
【python绘图—colorbar操作学习】
springboot+vue+Elementui班级事务管理系统
 vue模板语法02
Java之File类的详细解析及小练习
 java毕业设计教师档案管理系统mybatis+源码+调试部署+系统+数据库+lw
用友第五届开发者大赛初赛晋级公示，复赛火热进行中！
原文地址：https://blog.csdn.net/m0_61820867/article/details/126548376

数据结构——树