线性代数学习笔记7-1：特征值、特征向量、迹、特征基

特征向量：经历特定线性变换后，只受到伸缩影响的特殊向量

首先注意前提：特征值和特征向量，仅针对方阵讨论，因为非方阵不可能满足定义式$\mathbf{A}\vec{v}=\lambda \vec{v}$的维度要求

特征向量（Eigenvectors）$\vec{v}$：线性变换后，仍保持在其原张成空间内的向量(方向不变或反向)
特征值（Eigenvalue）$\lambda$：衡量特征向量在线性变换中被拉伸/压缩的比例因子
它们之间的关系记作：$$\mathbf{A}\vec{v}=\lambda \vec{v}$$

• 特别注意，特征值$\lambda =0$的特征向量，意味着它是$\mathbf{A}\vec{v}=0$的解，则特征向量$\vec{v}$位于$\mathbf{A}$的零空间中；
  另外，假如$\mathbf{A}$不可逆/奇异/不满秩，则零空间不只有零向量，即特征值$\lambda =0$的特征向量有无数个（$\mathbf{A}$对应降维的线性变换，有大量非零向量被压缩为零向量）

考虑一个变换，其i轴被拉伸，其j轴向i轴倾斜，我们可以写出对应的变换矩阵

考虑一个向量$\vec{v}=[2,1{]}^T$
在变换前，它的张成空间span为其所在的直线；
在变换后，由于整个空间的“压缩”，这个向量离开了它原先的张成空间

另一方面，也的确存在一些特殊的向量，在变换后留在其原来张成的空间内
线性变换对这些向量的作用，仅是压缩/拉伸，就好像是一个标量的作用一样

• x轴上的所有向量留在原span内，容易理解
• 隐蔽的是，处于变换后的新坐标系的基向量张成的对角线上的任意向量，例如(-1, 1)，同样留在其span内

举例理解特征向量

Eg1. 对于所有列向量线性无关的矩阵$\mathbf{A}$，他代表了一个平面，而投影矩阵$\mathbf{P}=\mathbf{A}({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T$能够将平面外的向量投影到平面上，例如将向量$\mathbf{b}$投影到平面上得到的$\mathbf{p}=\mathbf{P}\mathbf{b}=\mathbf{A}({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{b}$

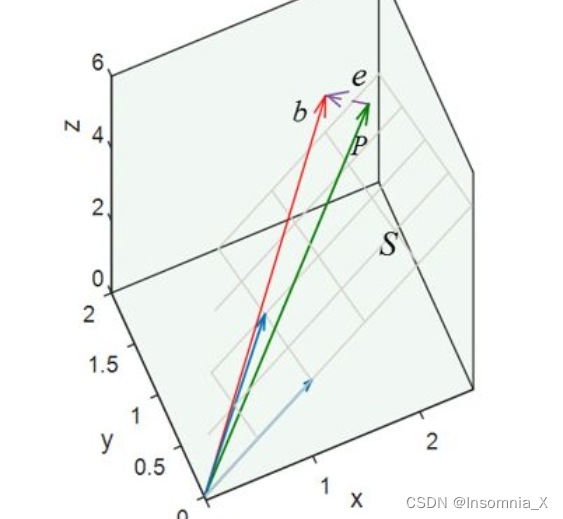
现在，求投影矩阵$\mathbf{P}$的所有特征值和特征向量

• 矩阵$\mathbf{A}$对应的平面（列空间）上所有向量都是特征值$\lambda =1$特征向量：$\mathbf{A}\vec{v}=\vec{v}$
• 垂直于平面的所有向量（零空间，与列空间互相正交），都是特征值$\lambda =0$特征向量：$\mathbf{A}\vec{v}=0$
• 注意，这里由于投影矩阵是对称矩阵，故行空间=列空间，又因为零空间与行空间间互为正交补，所以这里零空间与列空间间互为正交补，故：$\mathbf{P}$的特征向量互相垂直，所有特征向量张成了整个空间

Eg2. 置换矩阵$A=\left[\begin{array}{ll}0& 1\\ 1& 0\end{array}\right]$，其作用是将向量的两行位置互换，求其所有特征值和特征向量

• 就是要寻找互换两坐标后，仍在同一直线上的向量
• 向量 [ 1 1 ] \left[
  11" role="presentation" style="position: relative;">11$$\begin{array}{l}1\\ 1\end{array}$$
  \right] [11​]是特征值$\lambda =1$特征向量：$\mathbf{A}\vec{v}=\vec{v}$
• 向量 [ 1 − 1 ] \left[
  1−1" role="presentation" style="position: relative;">1−1$$\begin{array}{l}1\\ -1\end{array}$$
  \right] [1−1​]是特征值$\lambda =-1$特征向量：$\mathbf{A}\vec{v}=-\vec{v}$
• 这些特征向量张成了整个空间
• 因为是对称矩阵，其特征向量互相垂直

给出矩阵（某种变换），求解其特征向量

进一步的，要求解某个变换矩阵对应的特征向量$\vec{v}$
就是求下面方程的解(其中$\vec{v}$是待求解的量，并且需要非零解)：$$(\mathbf{A}-\lambda \mathbf{I})\vec{v}=0$$

• 根据求解齐次线性方程组的知识，该方程必有一个解是零向量，然而这个解无意义，我们需要的是非零解
  上式有非零解$\Rightarrow$，仅当$det(\mathbf{A}-\lambda \mathbf{I})=0$，即矩阵$(A-\lambda I)$不可逆/奇异，或线性变换使得空间被压缩降维
• 对于$det(\mathbf{A}-\lambda \mathbf{I})$，这是一个关于未知量$\lambda$的多项式$f(\lambda )$，称为特性多项式
• 综上，这个问题，最终变为：寻找合适的$\lambda$值，使得$det(\mathbf{A}-\lambda \mathbf{I})=0$成立，然后再带入特定的$\lambda$值，求解$(\mathbf{A}-\lambda \mathbf{I})\mathbf{x}=0$得到特征向量$\mathbf{x}$（利用消元法，求主元列和自由列…）
  这里由于$det(\mathbf{A}-\lambda \mathbf{I})=0$，可以看出，对于每个特征值$\lambda$，矩阵$(\mathbf{A}-\lambda \mathbf{I})$必为不可逆矩阵/奇异矩阵，从而方程有无数个非零解/存在（非零的、有效的）特征向量
  也就是说，任何特征值，都对应一个特征子空间（而不仅仅是一个特征向量）

注意：一般与特征向量对应的特征值都是实数
而特征值为虚数的情况，对应于变换中出现了某种旋转（例如对于旋转90°矩阵求特征值为$\mathbf{i}$,联系复平面内乘以$\mathbf{i}$的效果）

特征值和特征向量有什么用？

• 考虑三维空间中的三维向量，用一个3x3矩阵对其做“旋转”的线性变换，如果能找到这个变换中的特征值为1的特征向量（在变换过程中，始终留在其张成空间内的向量），那么就找到了旋转轴！（进一步可以将旋转视为绕轴一定角度的旋转，这比矩阵描述更直观）
• 并且，之前将矩阵的列向量看作基向量去向的做法，非常依赖于当前所用的坐标系（在其他的坐标系下，同一矩阵表示的变换完全不同），而特性向量则避开了对特定坐标系的依赖，只关注变换的特性本身

特征值的性质

• 任意$n\times n$矩阵，一定有$n$个特征值，但其中可能有重复的特征值
• 特征值的物理意义：物体都有一个自身的内禀结构，特征向量显示了物体内结构的方向，特征值则是在这个主方向上物体对外场的响应参数，也称伸缩系数，实际上它反应了在其所对应的特征向量方向上，内结构与外场之间的相互关系。
• 特征值可以作为降维的判据：降维的线性变换，矩阵不可逆/行列式为0$\Rightarrow$至少存在一个特征值为零（对应的特征向量就是方程Ax=0解/A的零空间中的所有向量）
  数学上理解，奇异矩阵的齐次方程有无穷个非零解；几何上理解，奇异矩阵对应了降维的线性变换，从而有许多向量被变为零向量（也就是特征值为零的特征向量）

应用：在图像压缩过程中，极小的特征值会被赋值为0，从而节省存储空间，降维后的图像基本轮廓依旧清晰，图像细节有所牺牲

• 迹trace=${\lambda }_1+{\lambda }_2+...+{\lambda }_n$=矩阵对角线上的元素之和
  这个性质可以用于求解未知的特征值
• 行列式=${\lambda }_1{\lambda }_2...{\lambda }_n$
  对于特征多项式因式分解，可以直观看出每一项对应一个根，从而对于二阶方阵，其特征多项式就是${\lambda }^2-trace(\mathbf{A})\lambda +det(\mathbf{A})=0$
• 对称矩阵的特征向量正交，因为对称矩阵对角化后，得到正交矩阵$\mathbf{A}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{-1}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^T$
  证明：设对称矩阵$\mathbf{A}$满足$\mathbf{A}{x}_1={\lambda }_1{x}_1$、$\mathbf{A}{x}_2={\lambda }_2{x}_2$
  第一个式子同乘$x_2^T$则有$x_2^T\mathbf{A}{x}_1={\lambda }_1{x}_2^T{x}_1$，又由第二个式子得到$x_2^T\mathbf{A}{x}_1=({\mathbf{A}}^T{x}_2{)}^T{x}_1=(\mathbf{A}{x}_2{)}^T{x}_1={\lambda }_2{x}_2^T{x}_1$，
  从而有$({\lambda }_1-{\lambda }_2)x_2^T{x}_1=0$，又${\lambda }_1\ne {\lambda }_2$，故$x_2^T{x}_1=0$，两特征向量正交
• 三角矩阵的特征值就是矩阵对角线上的元素
  原因：三角阵的特征多项式$det(\mathbf{A}-\lambda \mathbf{I})=0$，该行列式为上三角的，因此行列式就等于对角元上元素的乘积，从而$\mathbf{A}$的对角线元素就是特征多项式的根

例如对于三角阵$\mathbf{A}=\left[\begin{array}{ll}3& 1\\ 0& 3\end{array}\right]$，可以解得${\lambda }_1={\lambda }_2=3$，两者对应同一个特征向量${\mathbf{x}}_1=\left[\begin{array}{l}1\\ 0\end{array}\right]$；

• 特征值有重根，特征向量可能线性相关，此时意味着矩阵$\mathbf{A}$是一个退化矩阵（特征向量短缺，对应降维的线性变换）
  出现重复的特征值，我们认为这是一种“最坏”的情况
• $\mathbf{A}$特征值为$\lambda$，则$\mathbf{A}+k\mathbf{I}$的特征值为$\lambda +k$
  证明：原来的特征值满足$det(\mathbf{A}-\lambda \mathbf{I})=0$，那么$det[(\mathbf{A}+k\mathbf{I})-{\lambda }^{\prime }\mathbf{I}]=0$的解为${\lambda }^{\prime }=\lambda +k$
  注意，这条性质仅对于$\mathbf{A}+k\mathbf{I}$生效，一般$\mathbf{A}+\mathbf{B}$的特征值并不是各自特征值之和
• $\mathbf{A}$和${\mathbf{A}}^T$的特征值相同
  原因：由于矩阵的转置后行列式不变，则$det(\mathbf{A}-\lambda \mathbf{I})=0⟺det({\mathbf{A}}^T-\lambda \mathbf{I})=0$，故$\mathbf{A}$和${\mathbf{A}}^T$的特征值相同，但是其对应的特征向量不同，因为$\mathbf{A}$和${\mathbf{A}}^T$的特征向量在$(\mathbf{A}-\lambda \mathbf{I})$的零空间和左零空间中，即特征向量分别为方程$(\mathbf{A}-\lambda \mathbf{I})\mathbf{x}=0$的非零解和$(\mathbf{A}-\lambda \mathbf{I}{)}^T\mathbf{x}=0$的非零解
• 若$\mathbf{A}$特征值为$\lambda$，则${\mathbf{A}}^2$特征值为${\lambda }^2$
  证明：对任意矩阵，有$\mathbf{A}=\mathbf{M}\mathbf{J}{\mathbf{M}}^{-1}$，其中$\mathbf{J}$为约尔当型，则${\mathbf{A}}^2=\mathbf{M}{\mathbf{J}}^2{\mathbf{M}}^{-1}$，可证
  几何理解：两次线性变换，效果叠加，则特征向量缩放两次，特征值变为${\lambda }^2$

特征值的虚实性

分三种情况：

• 对称矩阵：实数的特征值，有一组正交的特征向量

例如对于$\mathbf{A}=\left[\begin{array}{ll}3& 1\\ 1& 3\end{array}\right]$，特征值和特征向量${\lambda }_1=4,{\mathbf{x}}_1=\left[\begin{array}{l}1\\ 1\end{array}\right]$，${\lambda }_2=2,{\mathbf{x}}_2=\left[\begin{array}{c}-1\\ 1\end{array}\right]$
注意，这里与前面的${\mathbf{A}}_0=\left[\begin{array}{ll}0& 1\\ 1& 0\end{array}\right]$对比，其${\lambda }_1=1,{\mathbf{x}}_1=\left[\begin{array}{l}1\\ 1\end{array}\right]$，${\lambda }_2=-1,{\mathbf{x}}_2=\left[\begin{array}{c}-1\\ 1\end{array}\right]$，可见由于$\mathbf{A}={\mathbf{A}}_0+3\mathbf{I}$，对应的特征值也加3，特征向量不变，但这个结论不是普遍成立，即两个矩阵的和的特征值不是两特征值直接相加，因为特征向量很可能并不相同因

• 反对称矩阵/斜对称矩阵（anti-symmetric matrices/skew-symmetric matrices，即${\mathbf{A}}^T=-\mathbf{A}$）：纯虚数的特征值，有一组正交的特征向量

例如对于正交矩阵$\mathbf{Q}=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}\cos 90^{\circ }& -\sin 90^{\circ }\\ \sin 90^{\circ }& \cos 90^{\circ }\end{array}\right]$，该矩阵对应了90°的旋转变换，应该不存在只受伸缩的特征向量（没有实数特征值），可以解得${\lambda }_1=i\text{ 和 }{\lambda }_2=-i$

• 介于两者之间的矩阵：有实数特征值，也有复数的特征值

特征值若为复数，则一定共轭成对出现，即两个共轭复数必然同时为特征值

实数特征值对应特征向量的伸缩，虚数特征值对应特征向量的旋转

特征向量的性质

• 当满足${\mathbf{A}}^T\mathbf{A}=\mathbf{A}{\mathbf{A}}^T$，则矩阵$\mathbf{A}$必然具有正交的特征向量
  典型的例子就是对称矩阵（包括正交矩阵）和反对称矩阵

迹

• 迹trace=${\lambda }_1+{\lambda }_2+...+{\lambda }_n$=矩阵对角线上的元素之和

迹实际上是一种是相似不变量（它仅由线性变换决定，但具体可以表现为多个相似矩阵），它就像是线性变换在矩阵中留下的“痕迹”

• 对于同一个线性变换，假如我们依赖的坐标系/基向量不同，这个变换对应的矩阵也就不同，但这两个矩阵是相似矩阵
• 相似矩阵的迹相同（迹与坐标系的选择无关）
• 类似的，特征值、行列式（描述某个变换的面积/体积缩放比例）、秩（描述列空间的维数）都是相似不变量

为什么会有相似不变量？

抓住核心：相似矩阵，始终描述同一个线性变换，因此这个线性变换虽然有不同的表现形式（相似矩阵），但其某些核心特性是固定了的

根据 特征值分解，矩阵$\mathbf{A}={\mathbf{P}}^{-1}\mathbf{\Lambda P}$，其中$\Lambda$为$daig({\lambda }_1,{\lambda }_2,...,{\lambda }_n)$，而$P$为对应的特征向量组成的矩阵，显然这里$A$和$\Lambda$也是相似矩阵，可见，$\Lambda$将同一个线性变换对应的各个相似矩阵联系起来（不同的相似矩阵，$\Lambda$相同，i.e.它们都有相同的特征值，但$P$不同，因为同一个变换，特征向量缩放比例一致，但是不同坐标系下观察到的特征向量不同）

进一步的，不同相似矩阵，其特征值固定，才导致了：

• 迹=${\lambda }_1+{\lambda }_2+...+{\lambda }_n$是相似不变量
• 行列式=${\lambda }_1\cdot {\lambda }_2\cdot ...\cdot {\lambda }_n$是相似不变量

同一个变换，不管在什么坐标系下进行（表现为不同的相似矩阵），其“核心特性”——特征值始终不变，（这就是为什么要称之为“特征”），特征值不变也决定了行列式、迹不变，他们都是相似不变量