如何评价一个算法的优劣——时间复杂度

算法复杂度包括时间复杂度和空间复杂度。好算法的评判标准就是高效率和低存储，高效率即时间复杂度小，低存储即空间复杂度小。

时间复杂度指算法运行需要的时间。

一般将算法的基本运算执行次数作为时间复杂度的度量标准。

举个栗子：

int sum(int n){
	int sum = 0; //1次
	for(int i = 1 ; i <= n ; i <++{ // n + 1次
		sum += i; // n次
	}
	return sum; //1次
}
1
2
3
4
5
6
7

总的执行次数为 2 x n + 3。

用一个函数T(n) = 2n + 3表示，算法运行时主要取决于最高项。

→ 如果用时间复杂度的渐进上界O表示，那么该算法的时间复杂度为O(n)。

其实没有必要计算每一行代码的运行次数，只需要计算语句频度最多的语句即可。

再举个栗子：

sum = 0; // 运行1次
total = 0; //运行1次
for(int i = 0 ; i <= n ; i++){ //运行n + 1次，最后1次判断条件不成立，结束。
	sum += i; //运行n次
	for(j = 1; j <= n ; j ++){ // 运行n*(n+1)次
		total = total + i * j; //运行n * n次
	}
}
1
2
3
4
5
6
7
8

循环内层的语句往往是运行次数最多的，对运行时间“贡献”最大。

在上面那个栗子中，total = total + i * j 最大，所以只需要计算语句的运行次数即可，该算法的时间复杂度为O(n ^ 2)。

常见的算法时间复杂度如下：

1. 常数阶：算法运行的次数是一个常数，O(1)
2. 对数阶：时间复杂度运行效率较高，常见的有O(logn)、O(nlogn)。
3. 多项式阶：很多算法的时间复杂度是多项式，常见的有O(n)、O(n^2)、O(n ^ 3)
4. 指数阶：指数阶时间复杂度运行效率极差。常见的有O(2 ^ n)、O(n!)、O(n ^ n)

常见的时间复杂度函数曲线：

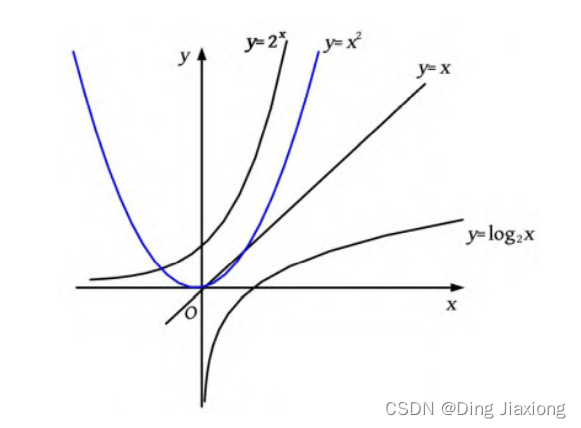
它们的关系是：

O(1) < O(logn) < O(n) < O(nlogn) < O(n ^ 2) < O(n ^ 3) < O(2 ^ n) < O(n !) < O(n ^ n)