神经网络（七）优化与正则化

神经网络（七）优化与正则化

一、定义

优化：经验风险最小（期望风险难以计算）

正则化：降低模型复杂度（防止过拟合）

二、网络优化

难点： ①结构差异较大（没有通用优化算法、超参数较多）

②非凸优化（参数初始化、逃离局部最优/鞍点）

③梯度消失/爆炸问题

1.高维空间中的非凸优化问题

鞍点：梯度为0的点

平坦最小值：在一个邻域内，所有点对应的训练值都比较接近。

大部分的局部最小解都是等价的；

局部最小解的训练损失可能非常接近全局最小解对应的训练损失

        2.优化地形的可视化

优化地形：高维空间中损失函数的曲面形状。



3.改善方法

①更有效的优化算法来提高优化方法和效率和稳定性

动态学习率调整、梯度估计修正

②更好的参数初始化、数据预处理方法以提高优化效率

③修改网络结构以获得更好的优化地形

使用ReLU激活函数、残差连接、逐层归一等

④使用更好的超参数优化方法

三、优化算法的改进

1.随机梯度下降

①小批量随机梯度下降

                (充分利用GPU的并行计算能力，每次更新一批参数)

step1：选取K个训练样本，计算偏导数

                                 $g_t(\theta)=\frac{1}{K}\sum_{(x,y\in S_t)}\frac{\partial L(y,f(x;\theta))}{\partial \theta}$

step2：定义梯度

                                 $g_t=g_t(\theta_{t-1})$

step3：更新参数（反向更新）

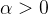                                 $\theta_t\leftarrow \theta_{t-1}-\alpha g_t$          $\alpha >0$ 称学习率

影响的关键因素：

1.样本数量K：不影响随机梯度的期望，但是会影响方差

                                                K越大，方差越小

                                                K较大时可以设置大学习率，引入噪声提升训练稳定性

                                                K较小时可以设置小学习率，否则会出现不收敛的现象

K值与学习率的关系：线性缩放规则。

K值对收敛的影响：

K值较大时，计算效率提升，迭代效率可能下降（单步较慢）

K值越小，模型泛化能力越强

一般来说K可以设置得更大（样本数量足够时）

2.梯度：以“加权移动平均”作为参数更新的方向（动量化）

                                                         $\Delta \theta_t=\rho \Delta\theta_{t-1}-\alpha g_t$

梯度截断

3.学习率：动态学习率 $\Delta \theta_t=-\frac{\alpha}{\sqrt{G_t+\epsilon }}\bigodot g_t$          随时间递减

②动态学习率

                        应用于小批量随机梯度下降

理想状态：一开始步长尽可能大，接近最优解时应当减小以免过冲

学习率衰减： 阶梯衰减、线性衰减

逆时衰减： $\alpha=\alpha_0\frac{1}{1+\beta \times t}$

指数衰减： $\alpha_t=\alpha_0\beta^t$

自然指数衰减： $\alpha_t=\alpha_0exp(-\beta \times t)$

余弦衰减： $\alpha_t=\frac{1}{2}\alpha_0(1+cos(\frac{t\pi}{T}))$

周期性学习率调整：三角循环学习率、带热重启的余弦衰减（整体递减）

周期性调整的原因：为了跳出局部最优

③其他学习率调整方法

增大批量大小(K与 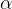$\alpha$ 正相关)

                        学习率预热（初始化时梯度不稳定）

自适应学习率

        ④梯度估计修正

1.动量法

        用之前累积的动量代替真正的梯度

                                         $\Delta\theta_t=\rho\Delta\theta_{t-1}-\alpha g_t=-\alpha \sum_{\tau=1}^t\rho^{t-\tau}g_t$

负梯度的“加权移动平均”；每次迭代的梯度可以看作是加速度，可以近似看作二阶梯度。

        2.Nesterov加速梯度

                                 $\Delta\theta_t=\rho\Delta_{t-1}-\alpha g_t(\theta_{t-1}+\rho\Delta\theta_{t-1})$

3.Adam算法

动量法+RMSprop

step1：计算两个移动平均

                                         $M_t=\beta_1M_{t-1}+(1-\beta_1)g_t$

                                         $G_t=\beta_2G_{t-1}+(1-\beta_2)g_t\bigodot g_t$

step2：偏差修正

                                         $\hat{M_t}=\frac{M_t}{1-\beta_1^t}$          $\hat{G_t}=\frac{G_t}{1-\beta_2^t}$

step3：更新

                                         $\Delta\theta_t=-\frac{\alpha}{\sqrt{\hat{G_t}+\varepsilon }}\hat{M_t}$

4.梯度截断(用于解决梯度爆炸问题)

按值截断：值处于[a,b]区间内

按模截断： $g_t=\frac{b}{||g_t||}g_t$ 模值最大为b

2.小结

大部分优化算法可以描述为：

                         $\Delta\theta_t=-\frac{\alpha_t}{\sqrt{G_t+\varepsilon }}M_t$

                         $G_t=\psi (g_1,...,g_t)$          $M_t=\phi (g_1,...,g_t)$

                         $\alpha_t$ 为t步的学习率 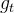       为t步的梯度

四、参数初始化

参数不能初始化为0，会造成对称权重问题（回传参数时，第一层的所有神经元都保持一致，无法判别其权重，会导致神经网络丧失能力）

初始化方法：①预训练初始化 ②随机初始化 ③固定值初始化（偏置通常0初始化）

1.随机初始化

高斯分布：参数从一个固定均值和固定方差的高斯分布进行随机初始化

均匀分布：参数在区间[-r,r]内采用均匀分布进行初始化

范数保持性：为了避免梯度爆炸/梯度消失问题，误差项应尽可能=1（不放大/缩小）

                         $||\delta^{(l-1)}||^2=||\delta^{(l)}||^2=||(W^{(l)})^T\delta^{(l)}||^2$

          基于方差缩放的参数初始化

正交初始化

                                 $W^{(l)}(W^{(l)})^T=I$

step1：用均值为0、方差为1的高斯分布初始化一个矩阵

step2：将这个矩阵用奇异值分解得到两个正交矩阵（使用其中之一作为权重矩阵）--通常用于RNN

五、数据预处理

1.尺度不变性

算法在缩放全部或部分特征后不影响学习和预测。

不同输入特征的尺度差异过大时会造成以下困难：

                        1.参数初始化较为困难

2.优化效率

2.规范化

①最小最大值规范化

                         $\hat{x}^{(n)}=\frac{x^{(n)}-min_n(x^{(n)})}{max_n(x^{(n)})-min_n(x^{(n)})}$

②标准化

                         $\hat{x}^{(n)}=\frac{x^{(n)}-\mu}{\sigma }$ 其中 $\mu=\frac{1}{N}\sum_{n=1}^Nx^{(n)}$          $\sigma^2=\frac{1}{N}\sum_{n=1}^N(x^{(n)}-\mu)^2$

③PCA(计算较为复杂，一般不使用标准化就够了)

3.逐层规范化

目的：更好的尺度不变性；内部协变量偏移(激活值分布随参数变化而变化)；更平滑的优化地形。

①批量规范化

第 l 层神经网络为： $a^{(l)}=f(z^{(l)})=f(Wa^{(l-1)}+b)$

给定K个样本的小批量集合，方差和均值为：

                                 $\mu_B=\frac{1}{K}\sum_{k=1}^Kz^{(k,l)}$          $\sigma^2_B=\frac{1}{K}\sum_{(k=1)}^K(z^{(k,l)}-\mu_B)\bigodot (z^{(k,l)}-\mu_B)$

批量规范化： $z^{(l)}=\frac{z^{(l)}-\mu_B}{\sqrt{\sigma^2_B+\varepsilon }}\bigodot \gamma+\beta$

优点：提高优化效率；隐形的正则化优化方法(使得神经网络不会过分依赖某个样本，从而提高网络的泛化能力)

缺点：小批量样本不能太小；无法应用到循环神经网络

②层规范化

第 l 层神经元的净输入为 $z^{(l)}$

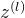
                                 $\mu^{(l)}=\frac{1}{M_l} \sum^{M_l}_{i=1}z^i^{(l)}$          $\sigma^{(l)^2}=\frac{1}{M_l}(z_i^{(l)}-\mu^{(l)})^2$

层规范化定义

                                 $z^{(l)}=\frac{z^{(l)}-\mu^{(l)}}{\sqrt{\sigma^{(l)^2}+\varepsilon }}\bigodot \gamma+\beta=LN_{\gamma,\beta}(z^{(l)})$

4.超参数优化

超参数：层数、每层神经元个数、激活函数、学习率、正则化稀疏、mini-batch大小

①网格搜索

假设共K个超参数，第k个超参数可以取个值，并穷举每种组合。

若超参数连续，则需要将其离散化（不等距离）

②随机搜索

③其他方法

贝叶斯优化、动态资源分配、神经架构搜索

六、正则化

所有损害优化的算法。包括：

①增加优化约束(L1/L2约束、数据增强)

②干扰优化过程(权重衰减、随机梯度下降、早停法、暂退法)

1.早停法

引入一个验证集，每迭代一次使用验证集测试一次，若验证集错误率不再下降，则停止优化。

2.权重衰减

通过限制权重的取值范围，降低模型能力

每次更新参数时，引入一个衰减系数 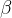$\beta$ ,(一般取值较小，如0.0005)

                         $\theta _t\leftarrow (1-\beta)\theta_{t-1}-\alpha g_t$

3.暂退法

神经层：

引入一个掩蔽函数使：         $mask(x)=m\bigodot x$ (m为掩码，值域区间{0,1}，使用概率为p的贝努利分布随机生成)

会造成训练和测试时网络的输出不一致的问题，可以对测试集降维

暂退法提升网络正则化的解释：

①集成学习的解释

每进行一次暂退，相当于从原始网络中采样得到一个子网络,最后使用的可以视为2^n个子网络的集成 $l_p(\theta)\leq 1$

②贝叶斯学习的解释

                         $E_{q(\theta)}[y]=\int _q=f(x;\theta)q(\theta)d\theta\approx \frac{1}{M}f(x,\theta_m)$

暂退法一般不能直接应用在循环神经网络（会损害其记忆能力）

变分暂退法

对参数矩阵的每个约束进行随机暂退，所有时刻使用同样的暂退掩码

4.l1和l2正则化

优化问题可以写作： $\theta^*=arg_\theta min\frac{1}{N}\sum_{n=1}^N L(y^{(n)},f(x^{(n)}))+\lambda l_p(\theta)$

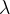其中为规范函数：l1和l2范数         $\lambda$ 为正则化系数

目标是使 $l_p(\theta) \leq 1$ 需要使得l1,l2的绝对值小于1

标准的随机梯度下降中，l2正则化等价于权重衰减

5.数据增强

人工构建新的样本来增加训练数据的数量和多样性

①对x的增强

                        采用旋转、翻转、缩放、平移、加噪声等方式来增强图像数据

        采用词汇替换、回译、随机编辑噪声（增删改查、句子乱序）来增强文本数据

②对y的增强

标签平滑：在输出标签中添加噪声来避免过拟合

                         $y=[0,...,0,11,0...,0]^T\rightarrow [\frac{\varepsilon }{K-1},...,\frac{\varepsilon }{K-1},1-\varepsilon ,\frac{\varepsilon }{K-1},...,\frac{\varepsilon }{K-1}]$
相关阅读:
ARM接口实验—中断实验
 订阅发布和请求响应都是消息传递模式
 Go短网址项目实战---上
 [计算机网络基础]物理层详解
 如何在 Microsoft IIS 服务器中配置自定义 404 错误页面
 千峰商城-springboot项目搭建-82-订单提交及支付-支付回调
 Linux内核netLink套接字
 unity打AB包，AssetBundle预制体与图集（二）
基于Java的药品商城管理系统设计与实现(源码+lw+部署文档+讲解等)
FPGA/HDL 开发的 10 条规则
原文地址：https://blog.csdn.net/weixin_37878740/article/details/126498070

一、定义

二、网络优化

1.高维空间中的非凸优化问题

2.优化地形的可视化

3.改善方法

三、优化算法的改进

1.随机梯度下降

①小批量随机梯度下降

②动态学习率

③其他学习率调整方法

④梯度估计修正

2.小结

四、参数初始化

1.随机初始化

五、数据预处理

1.尺度不变性

2.规范化

3.逐层规范化

①批量规范化

②层规范化

4.超参数优化

①网格搜索

②随机搜索

③其他方法

六、正则化

1.早停法

2.权重衰减

3.暂退法

4.l1和l2正则化

5.数据增强

①对x的增强

②对y的增强