阵列信号处理——LMS自适应波束形成算法

一、LMS自适应波束形成算法 

最小均方算法（LMS）采用迭代模式，在每个迭代步骤n时刻的权向量加上一个校正量后，即组成n + 1时刻的权向量，用它逼近最佳权向量。LMS自适应波束形成算法如下表所示：

二、自适应波束形成的最佳权矢量
一般来说，并不希望直接求解方程，其理由如下：①由于移动用户环境是时变的，所以权向量的解必须能及时更新；②由于估计最佳解需要的数据是含噪声的，所以希望使用一种更新技术，可利用已求出的权向量求平滑最佳响应的估计，以减小噪声的影响。因此，希望使用自适应算法周期更新权向量。实际上就是自适应滤波的工程，使得输出不断向期望信号收敛。这里以MMSE（最小均方误差）为例，说明如何把他变成一种自适应算法。

1、MMSE方法
MMSE准则就是使误差y（k）-d（k）的均方值最小化，即代价函数取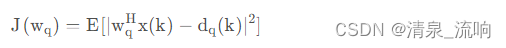

实际上就是数学中的问题，给了y，要去求使得y取得最小最小值的x，在一维中我们直接求导数就可以，在二维和高维中，我们利用雅可比行列式，实际上是和一元差不多。在一元函数中，我们寻找最优点往往就是先给定初始x，然后以一个步长往梯度的反方向步进，在这里也是一样。我们将上式子展开

 

上式对wq求导，得

只要求出了梯度，我们就可以迭代，一步一步沿着梯度的方向去步进。
2、LMS算法
MMSE方法可以用LMS算法实现。
考虑随机梯度算法，其更新权矢量的一般公式为

式中，u是收敛因子，实际上就是步长，这个步长，选长了，容易收敛不了，就一直在最优点旁边左右移动，选短了，需要的迭代次数增加。
上面已经求出

但是E这个东西是个什么呢？在实际运算中，我们如何求E呢？实际上E是一个总体的特征，当样本
足够多时，我们可以去估计它，但是我们现在要求实时更新，也就是采一次样，那么就利用LMS算法去更新一次，现在有E是不可以的，LMS算法的基本思路是把数学期望用各自的瞬时值代替，即得到k时刻的梯度估计值如下

实际上

即是的一个无偏估计，在某些情况下，我们是可以替代的。
我们将梯度值代回权矢量的更新公式，得到了LMS算法为

三、MATLAB代码实现 

1、代码逻辑

2、代码实现，程序如下

clear all
close all
clc
M=16;                  % 天线数
K=2;                   % 信源数
theta=[0 30];          % 信号入射角度
d=0.3;                 % 天线间距
N=500;                 % 采样数
Meann=0;   varn=1;     % 噪声均值、方差
SNR=20;
INR=20;
pp=zeros(100,N);pp1=zeros(100,N);
rvar1=sqrt(varn)*10^(SNR/20);        % 信号功率
rvar2=sqrt(varn)*10^(INR/20);        % 干扰功率
for q=1:100
    s=[rvar1*exp(1i*2*pi*(50*0.001*[0:N-1]));rvar2*exp(1i*2*pi*(100*0.001*[0:N-1]+rand))];  % 生成源信号
    A=exp(-1i*2*pi*d*[0:M-1].'*sin(theta*pi/180));   % 方向向量
    e=sqrt(varn/2)*(randn(M,N)+1i*randn(M,N));       % 噪声
    Y=A*s+e;                                         % 接收信号
    % LMS算法
    L=200;
    de=s(1,:);
    mu=0.0005;
    w=zeros(M,1);
    for k=1:N
        y(k)=w'*Y(:,k);                              % 预测下一个采样和误差
    e(k)=de(k)-y(k);                                 % 误差
    w=w+mu*Y(:,k)*conj(e(k));                        % 调整权向量
    end
end
 
% 波束形成
beam=zeros(1,L);
for i=1:L
    a=exp(-1i*2*pi*d*[0:M-1].'*sin(-pi/2+pi*(i-1)/L));
    beam(i)=20*log10(abs(w'*a));
end
 
% 作图
figure
angle=-90:180/200:(90-180/200);
plot(angle,beam);
grid on
xlabel('方向角/degree');
ylabel('幅度响应/dB');
figure
for k=1:N
    en(k)=(abs(e(k))).^2;
end
semilogy(en);hold on
xlabel('迭代次数');
ylabel('MSE');

运行结果如下：

参考文献：

https://blog.csdn.net/weixin_43601588/article/details/124312470?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166134186016782184615363%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=166134186016782184615363&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-2-124312470-null-null.142^v42^new_blog_pos_by_title,185^v2^tag_show&utm_term=LMS%E8%87%AA%E9%80%82%E5%BA%94%E6%B3%A2%E6%9D%9F%E5%BD%A2%E6%88%90%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187

阵列信号处理及MATLAB实现；张小飞，陈华伟，仇小锋（编著）