-
李代数求导
李代数求导是SLAM的基础,由于SLAM待求解的状态量包含旋转,而旋转状态量为了避免歧义,往往采用更高维的四元素或者旋转矩阵表示。为了通过优化的方法更新旋转状态量,需要求出旋转后的点关于旋转状态量的雅可比。
1. 李群李代数部分整理
1.1. 群的概念

1.2. SO(3)推导

在
 附近假设
附近假设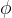 不变,可解微分方程可以得到:
不变,可解微分方程可以得到:
即

该式说明:
- 任意t都可以找到R与ϕ对应关系
- 该关系称为指数映射
- ϕ称为李代数
1.3. 李代数
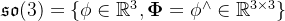


注: 不同书中对于se(3)中的顺序不一定都一样
1.4. 指数映射与对数映射



1.5. 伴随

SE(3)伴随

1.6. 求导与扰动
1.6.1. BCH公式与左右雅克比
李群对于加法不封闭,需要重新定义导数,解决方法两种:
- 利用李代数加法定义李群元素的导数
- 利用指数映射和对数映射完成变换关系

对于李群不成立,于是利用BCH公式:
左雅克比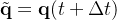

右雅克比

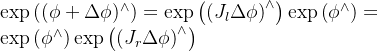
对于SE3形式更为复杂
对于旋转后的点坐标关于旋转的导数:

由于R没有加法,导数无法定义,于是如下解决方法:
- 对R对应的李代数加上小量,求相对于小量的变化率(导数模型)
- 对R左乘或者右乘一个小量,求相对于小量的李代数的变化率(扰动模型)
导数模型:
1.6.2. 需要计算雅克比矩阵
扰动模型:左扰动:
右扰动的推导类似.
SE(3)扰动模型

1.7. 补充


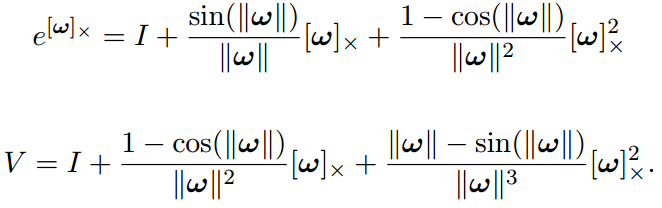
SO(3)重要性质与证明

1.8. 导数
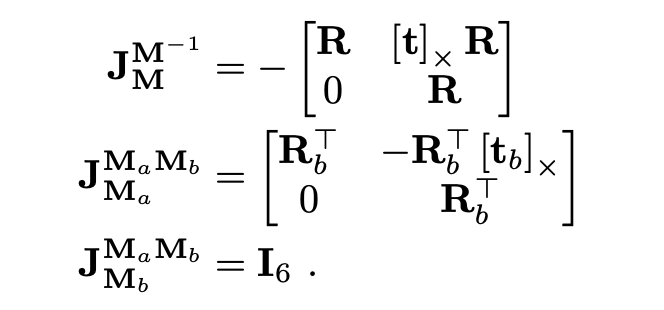

2. 四元数的两种不同形式
2.1. 分类
通常四元数分为JPL四元数和Hamilton四元数两种,JPL在航空中常用而Hamilton则在机器人领域较为常用,ROS、Eigen、Ceres中使用的都是Hamilton四元数.

实部顺序:
实际使用中,需要注意一下即可,仅在计算中有些差别
- Hamilton四元数实部在前,虚部在后
- JPL四元数实部是最后一个元素
-
左手系与右手系:

两种定义下的四元数是共轭关系:

旋转操作:
- 坐标轴(frame)不变,旋转的是向量,类似相机不动,相机所观察的目标在运动,称为:
Active Rotation - 向量不变,坐标轴在变化,类似相机视角在变,目标不动,一个向量v可以用不同坐标系下的坐标表示,即:
Passive Rotation - JPL和Hamilton都是Passive表示
旋转变换:

从数值上来看,JPL四元数和Hamilton四元数是相等的.
-
Local-to-Global: 将旋转后坐标系下的坐标变换到旋转前坐标系下
-
Global-to-Local: 将旋转前坐标系下的坐标变换到旋转后坐标系下
-
对于添加扰动的区别:Local-to-Global 是右扰动,Global-to-Local 是左扰动
2.2. 扰动
2.2.1. 局部扰动
Local-to-Global的形式下,局部扰动表示为:

2.2.2. 全局扰动
Global-to-Local形式下,全局扰动表示为:

2.3. 角速度

关于Barfoot中的四元数: Barfoot书中使用的四元数: 实部在后,右手系,Passive方式,左扰动
3. 旋转角速度
3.1. 扰动量的定义
局部扰动:
之所以乘在右边是由Hamilton形式四元数决定的. 从局部扰动可以获得对应在局部切空间的等效向量
 再利用指数映射:
再利用指数映射:
可以得到

如果扰动很小,那么可以进行近似,有如下结果:
![\large \large \Delta q_{{\mathcal{L}}} \approx \begin{bmatrix} 1 \\ \frac{1}{2}\Delta \phi_{{\mathcal{L}}} \end{bmatrix}, \Delta R_{\mathcal{L}}\approx I+[\Delta \phi_{\mathcal{L}}]_{\times}](https://1000bd.com/contentImg/2023/06/15/031717861.png)
扰动量为对应的$SO(3)$流形处切空间的元素,方便去定义协方差矩阵.
全局扰动
扰动值:

对应原点处的切空间元素。
3.2. 对时间的导数
局部扰动求导:初始状态
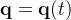 扰动状态为
扰动状态为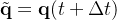 求导公式可得:
求导公式可得:
 为q所在的局部坐标系的角速度向量对应的的局部扰动量,具体求导形式如下:
为q所在的局部坐标系的角速度向量对应的的局部扰动量,具体求导形式如下: 定义:
![\large \Omega(\omega)= [\omega]R=\begin{bmatrix} 0 & -\omega^T \\ \omega & -[\omega]{\times} \end{bmatrix}](https://1000bd.com/contentImg/2023/06/15/031716812.png)
可以得到:
![\large \dot{\mathbf{q}}=\frac{1}{2}\Omega(\omega_{\mathcal{L}})\mathbf{q}=\frac{1}{2}\mathbf{q}\otimes\omega_{\mathcal{L}}, \quad \dot{R}= R[\omega_{\mathcal{L}}]{\times}](https://1000bd.com/contentImg/2023/06/15/031716494.png)
可以看到,角速度

是在特定参考系中的量,可以从IMU传感器直接获取.
全局扰动求导:![\large \dot{\mathbf{q}}=\frac{1}{2}\omega_{\mathcal{G}}\otimes\mathbf{q}, \quad \dot{\mathbf{R}}=[\omega_{\mathcal{G}}]{\times}\mathbf{R}](https://1000bd.com/contentImg/2023/06/15/031716839.png)
其中:

对应全局坐标系下的角速度.
3.3. 局部与全局之间的变换关系

3.4. 利用Adjoint来变换
利用性质:

也可以得到对应的结果:
对于
![\large \dot{R}= R[\omega_{\mathcal{L}}]{\times}](https://1000bd.com/contentImg/2023/06/15/031717584.png)
![\large \dot{R}= R[\omega_{\mathcal{L}}]{\times} =[R\omega_{\mathcal{L}}]{\times}R=[\omega_{\mathcal{G}}]_{\times}R](https://1000bd.com/contentImg/2023/06/15/031718510.png)
4. 流形上的优化

参考文献
slam/liegroup/README.md · Zixin-YANG/SummerCamp - Gitee.com
g2o中 EdgeSE3Expmap类型Jacobian的计算_白巧克力亦唯心的博客-CSDN博客
A micro Lie theory for state estimation in robotics
-
相关阅读:
1. 开篇辞和一些SQL语句基本概念
什么是防火墙?详解三种常见的防火墙及各自的优缺点
php简单后门实现及php连接数据库
深入探究RTOS的任务调度
解决Github打开后排版紊乱问题
小型功率放大器的设计与制作——功率放大器的设计方法
Flutter:文件与网络操作摘要
CondaError: Downloaded bytes did not match Content-Length
【一起来学C++】————(10)STL之string容器
什么是JPA? JPA在springBoot中怎么使用
- 原文地址:https://blog.csdn.net/xhtchina/article/details/126495655