PriorityQueue的特点

priorityQueue建堆是小根堆

    public static void main(String[] args) {
        //默认是小根堆
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        priorityQueue.offer(45);
        priorityQueue.offer(12);
        priorityQueue.offer(55);
        priorityQueue.offer(66);
        System.out.println(priorityQueue.peek());
    }
1
2
3
4
5
6
7
8
9

如果要建堆为大根堆，那就要写比较器Comparator了

    public static void main(String[] args) {
       PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
           @Override
           public int compare(Integer o1, Integer o2) {
               return o2-o1;
           }
       });
    }
1
2
3
4
5
6
7
8

priorityQueue使用offer添加元素时，一定要明确比较的规则，然后再添加

使用offer前，必须告诉offer以什么方式比较添加

class Fruit implements Comparable<Fruit>{
    public int age;
    //必须告诉priorityQueue.offer 以什么方式比较添加元素
    @Override
    public int compareTo(Fruit o) {
        return this.age - o.age;
    }
}

    public static void main(String[] args) {
        PriorityQueue<Fruit> priorityQueue = new PriorityQueue<>();
        priorityQueue.offer(new Fruit() );
        priorityQueue.offer(new Fruit() );
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

不能插入null对象，否则会抛出NullPointerException异常

可以插入任意多个元素，会自动扩容，没有容量限制

插入和删除元素的时间复杂度为O(log n),建栈的时间复杂度O（n）

PriorityQueue几种常见的构造方式

创建一个空的优先级队列，默认容量是11
PriorityQueue() 初始默认容量为11
创建一个初始容量为initialCapacity的优先级队列，注意：
initialCapacity不能小于1，否则会抛IllegalArgumentException异
常
PriorityQueue(int initialCapacity)
用一个集合来创建优先级队列
PriorityQueue(Collection c)

优先级队列的扩容说明：
如果容量小于64时，是按照oldCapacity的2倍方式扩容的
如果容量大于等于64，是按照oldCapacity的1.5倍方式扩容的
如果容量超过MAX_ARRAY_SIZE，按照MAX_ARRAY_SIZE来进行扩容

优先级队列的应用

top-k问题

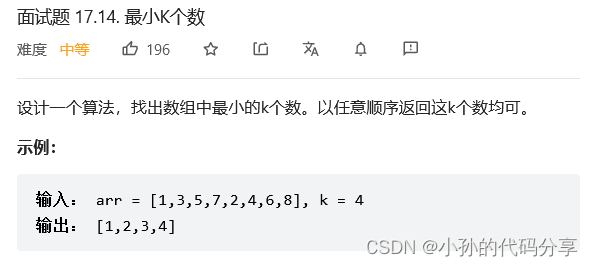最小k问题
应用优先级队列解法：

class Solution {
    public int[] smallestK(int[] arr, int k) {
       int[] ret = new int[k];
        if(k == 0) return ret;
        PriorityQueue<Integer> maxPQ = new PriorityQueue<>(k,new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2-o1;
            }
        });
 
        for (int i = 0; i < arr.length; i++) {
            if(maxPQ.size() < k) {
                maxPQ.offer(arr[i]);
            }else {
                //获取到堆顶元素
                int top = maxPQ.peek();
                //找前k个最小的
                if(arr[i] < top) {
                    maxPQ.poll();
                    maxPQ.offer(arr[i]);
                }
            }
        }
        for (int i = 0; i < k; i++) {
            ret[i] = maxPQ.poll();
        }
        return ret;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

最简单题解：

class Solution {
    public int[] smallestK(int[] arr, int k) {
        int[] arr1 = new int[k];
        Arrays.sort(arr);
        for (int i = 0; i < k; ++i) {
            arr1[i] = arr[i];
        }
        return arr1;
    }
}
1
2
3
4
5
6
7
8
9
10

2. 那如果要求第K大的元素，或者第K小的元素如何做

（1）前面求前K个最大的元素时，建立的小根堆，按照规则，到最后栈中全部都是前K个最大的元素，然后栈顶就是所要求得的第K大的元素 

（2）前面求前K个最小的元素时，建立的大根堆，按照规则，到最后栈中全部都是前K个最小的元素，然后栈顶就是所要求得的第K小的元素
1
2
3

优先级队列的特点就总结的差不多了，后面会对排序做一些总结和练习，希望可以对大家学习有所帮助吧