人工神经网络的算法原理,人工神经网络算法优点

其他定量分析方法

7.5.1多因子工程地质分析法7.5.1.1原理多因子工程地质分析法是由许惠德于1989年提出的。

该法主要考虑井田建造、层组、岩组特征，以及岩性变异特征、岩体质量优劣分段、构造变异特征、河谷卸压影响及水文地质条件等工程地质因素。

以岩组划分为基础，融合其他工程地质因素，采用对比分类法，将煤层顶板划分成4种稳定区域。7.5.1.2方法(1)地质因素分析1)建造:为一定的大地构造单元内，成岩作用在时间上的分异特征的术语。

2)层组:指不同岩性的岩层作有规律的组合，其划分是在建造基础上进行的。据煤系地层沉积特征，可划分出单层结构和多层结构两大类(表7.19)。

3)岩组:为岩体与岩石在一般特征上类似工程地质特征上相近的组合，其划分是在层组基础上进行的(表7.19)。

4)岩性变异特征:对煤层顶底板岩体可进行室内物理力学性质指标测定、室内微观分析(包括薄片鉴定、差热分析、X-射线衍射分析和电子显微镜分析)等。

如对山西谱庄矿3号煤层顶板分析后得出如下结论:①泥岩、粉砂岩不具膨胀性，粉砂岩中石英有被粘土矿物交代现象，具泥质结构和显微定向构造，基底式胶结，胶结物为泥质，与泥岩有相似的物理力学性质，强度较低;②在同一岩组中，岩石的强度有由井田北部向中偏南降低的趋势;③井田中部岩体破碎程度较高;④随深度增加，各类岩石的完整程度增高。

5)岩体质量优劣分级:以岩石质量指标(RQD)作为岩体质量优劣的半定性评价。如潘庄矿(图7.11)首采区的中上部岩体质量极坏，据此可提出整个块段岩体质量评价。

6)构造变异特征:根据地层倾角、构造发育、顶板岩性组成等，评价一个地区的构造应力状况。

如山西某井田内地层倾角平缓(5°～15°)，褶皱呈舒缓波状，无较大的断层存在，地震烈度不高(6度)，3号煤层的顶板大多为松软岩石。因此，井田内不易积聚大量应变能，构造应力较低。

表7.19潘庄一号井田工程地质岩组划分7)河谷卸压:河谷卸压会影响采场和巷道顶、帮内的应力分布;而应力的增加、岩体的膨胀、松弛、裂隙的产生均会加剧顶板和围岩的不稳定性。

如潘庄矿3号煤层首采区上方为一构造剥蚀的低山区，河谷两侧为侵蚀堆积地形。河谷切割较深，卸压现象较为严重。

因此，根据3号煤层上覆岩层的厚度(图7.11)和性质、顶板岩层的强度，预测了相对严重卸压区段。8)水文地质条件:主要根据地质、水文地质观测、试验资料，利用一定计算方法评价地质条件。

如山西某矿通过分析计算煤层顶板岩体冒落带和破裂带的最大高度值，认为虽然冒落带与上覆含水层连接，采场充水似乎不可避免，但由于含水层水量较小易于疏干，因此不会造成突水威胁。

(2)工程地质稳定性分区通过对各种地质因素的分析和对比，利用一定的计算和统计方法，应用综合编图手段，最终作出工程地质稳定性分区图，可划分出稳定区、中等稳定区、不稳定区和极不稳定区等4类，如果采用数学地质、数理统计、定量评价等手段，可以给上述4类区段赋予评价指数(参数)。

图7.12为潘庄矿首采区工程地质稳定性分区。

图7.11层理岩组图图7.12山西潘庄采区工程地质分区7.5.2顶板稳定性沉积模式研究法7.5.2.1原理该方法属成因顶板稳定性研究范畴，从沉积环境分析入手，分析顶板沉积模式，最终探明顶板稳定类型。

7.5.2.2方法步骤(1)顶板岩性分类首先要对某煤层顶板(研究对象)进行岩性分类，分类的资料基础主要是勘探钻孔资料。

如J.Truman等利用钻孔资料，将1号煤层以上10英尺(1英尺=0.3048m)的岩性划分成16种类型，并用3位数码表示各种岩石(图7.13)。

(2)编制岩性分布图编制煤层之上不同高程的岩性分布图。从图中可以清楚地了解煤层之上岩性在横向和纵向上的分布及其变化。图7.14为美国怀俄明州某矿l号煤层之上10英尺岩性分布图。

(3)工程应用J.Truman等通过研究美国怀俄明州某矿1号煤层顶板类型，认为在地下开采过程中，河道沉积物(图7.13中的层序类型l，4，9，10，11，12，13)顶板一般坚固稳定，如果河道砂岩没有切入煤层顶部(图7.13中层序类型⑨，⑩，瑏瑡，瑏瑢，瑏A)，则插入的页岩可能有擦痕面。

这些擦痕面是由于砂岩与页岩之问的致密程度不同而造成的，它们可能是引起顶板稳定性差异的重要因素，层序类型瑏A(流状沉积)发生在河曲的切割侧。

当发生滑动时，它们可使层理扭曲，大大降低了岩石强度，并常造成严重冒顶。一般来说，河道与河道之间的过渡带是不稳定的。

另外还要注意煤层顶面到河道砂岩底面之间的距离，以确保使用合适的顶板锚杆，从而使锚点放在砂岩的底部。

天然堤沉积(图7.13中层序类型⑥常含有植物根，这些植物根破坏了层理，降低了岩石的强度，必须加以锚固或强制冒落。

决口扇(图7.13中层序类型②，③)往往是煤层发育的台坪，从而产生一个软弱带。决口扇与煤层之间的间距以及决口扇的厚度应予以注意，以确保锚杆有足够的长度，使锚点在砂岩中或是薄煤层之上。

图7.131号煤层以上10英尺内的典型岩石层序(据J.Truman等，1985)①均质砂岩10英尺;②1号煤层直接顶板的决口扇砂岩厚度;③1号煤层以上2～3英尺的决口扇砂岩厚度;④324至124为向上变细层序(1号煤层以上的距离);⑤均质砂质页岩(324);⑥均质砂岩与页岩互层(124);⑦向上变粗层序;⑧均质页岩(124);⑨河道砂岩，厚度＜10英尺;⑩河道砂岩底部，大于10英尺，1号煤层以上0～4英尺;瑏瑡河道砂岩底部，＞10英尺，1号煤层以上4～6英尺;瑏瑢河道砂岩＞10英尺，1号煤层以上6～10英尺;瑏A1号煤层以上10英尺间隔内的流动构造;瑏A1号煤层以上0～4英尺的薄煤层;瑏瑥1号煤层以上4～6英尺的薄煤层;瑏瑦1号煤层以上6～10英尺的薄煤层015—炭质砂岩;020—煤层;124—粘土;324—砂质泥岩;544—砂岩图7.141号煤层以上10英尺内的岩石类型层序$（据J.Truman等，1985）$海湾沉积物(图7.13中层序类型⑤，⑦，⑧)一般是坚固稳定的。

稳定性最差的是(图7.13中层序类型（16）)1号煤层之上的薄煤层及其下伏层是被植物根穿透的页岩，为顶板弱带，最易发生离层，造成顶板不稳定。

7.5.3单项分析、综合评判法7.5.3.1原理和方法如前所述，影响煤层硬板稳定性的地质因素很多，多则十几项，少则四、五项。

对某一煤田或井田来说，所有因素中总是有主有次，因此需要逐一甄别，即单项分析，以筛选出几个主要因素，经过综合评判，然后与已采区实际揭露和顶板冒落情况进行对比，给予恰当的科学评分。

最后在综合图上据评分结果划出各种不同的区域。7.5.3.2步骤以山东新汶某矿第2煤层硬板为例，简述工作步骤。(1)单项地质因素分析1)岩性:第2煤层顶板岩性主要有砂岩、粉砂岩、页岩。

评判给分如表7.20所示。表7.20各单向因素评分注:括号中数字为评分。2)岩层厚度:岩层厚度是评判的主要参数，因此需据不同岩性、不同厚度分别评分。

对砂岩、粉砂岩、页岩等岩层厚度评判的评分结果见表7.20。3)倾角变异系数:在煤层构造图上采用“滑动窗口法”计算出倾角变异系数，然后分指标段给予评分(表7.20)。

4)小断层发育密度:同样采用“滑动窗口法”计算出小断层发育密度，未采区应先进行小断层发育规律及密度的预测，然后给予评分(表7.21)。

表7.21综合评判评分结果5)第2煤距上部第1煤的距离:第2煤层上部有的地方发育了一薄煤层(即第1煤层)。由于薄煤层是个软弱层，所以开采后最易发生离层而冒落。

而且，这种冒落的影响因素中最关键的是第2煤层距第1煤层的距离。据该矿历次实际冒落情况分析，给予表7.20所示评判记分。

(2)综合评判—稳定性区划据各次评判记分结果编图，经综合分析进行顶板稳定性区划，经与已采区的实际冒落情况对比基本吻合，最后成果见表7.21和图7.15。

图7.15第2煤层顶板稳定性分区7.5.4人工神经网络法7.5.4.1人工神经网络简介随着计算机技术的普及和发展，利用计算机进行顶板预测的研究大量出现，如利用模糊数学法(丁述礼，1994;王生全，1997;刘衡秋，2002)、层次分析法(刘海燕，2004)、模糊聚类法(涂敏，1995)、分形几何法(徐林生，1996;张玉三，1995)等方法来预测和评价顶板稳定性，并在相应方面和区域取得了明显的成效。

本节将用人工神经网络法建立顶板稳定性预测模型，预测龙固井田顶板稳定性，进一步做出顶板稳定性综合分区图。

(1)人工神经网络的起源人工神经网络(ArtificialNeuralNetwork，简称ANN)研究的先锋，美国心理学家WarrenS.McCulloch和数学家WalterH.Pitts曾于1943年提出一种叫做“似脑机器”(mindlikemachine)的思想，这种机器可由基于生物神经元特性的互联模型来制造，这就是神经学网络的概念。

他们构造了一个表示大脑基本组成部分的神经元模型，对逻辑操作系统表现出通用性。

随着大脑和计算机研究的进展，研究目标已从“似脑机器”变为“学习机器”，为此一直关心神经系统适应律的心理学家于1949年提出了学习模型。

1957年Rosenblatt首次提出感知器，并设计了一个引人注目的结构。

到60年代初期，关于学习系统的专用设计指南有Widrow等提出的Adaline(adaptivelinearelement，即自适应线性元)以及Steinbuch等提出的学习矩阵。

由于感知器的概念简单，因而在开始介绍时对它寄予很大希望。然而，不久之后Minsky和Papert从数学上证明了感知器不能实现复杂的逻辑功能。

到了70年代，Grossberg和Kohonen对神经网络研究做出了重要贡献。以生物学和心理学证据为基础，Grossberg提出了几种具有新颖特性的非线性动态系统结构。

该系统的网络动力学由一阶微分方程建模，而网络结构为模式聚集算法的自组织神经实现。基于神经元组织自己来调整各种各样的模式的思想，Kohonen发展了他在自组织映像方面的研究工作。

Werbos在70年代开发了一种反向传播算法。Hopfield在神经元交互作用的基础上引入一种递归型神经网络，这种网络就是有名的Hopfield网络。

在80年代中叶，作为一种前馈神经网络的学习算法，Parker和Rumelhart等重新发现了反回传播算法。如今，神经网络的应用越来越广泛了。

(2)人工神经网络的特点及应用人工神经网络是由许多神经元互连在一起组成的复杂网络系统。

它是在现代神经学研究成果基础上提出的，能模拟人的若干基本功能，具有并行分布的信息处理结构，通过“学习”或“训练”的方式完成某一特定的工作。

其最显著的特点是具有自学习能力，并在数据含有噪音、缺项或缺乏认知时能获得令人满意的结论，特别是它可以从积累的工作实例中学习知识，尽可能多地把各种定性、定量的影响因素作为变量加以输入，建立各影响因素与结论之间的高非线性映像，采用自适应模式识别方法完成此工作。

它对处理内部规律不甚了解、不能用一组规则或方程进行描述的较复杂问题或开放的系统显得较为优势。按照神经元的连接方式，人工神经网络可分为两种:没有反馈的前向网络和相互结合型网络。

前向网络是多层映像网络，每一层中神经元只接受来自前一层神经元的信号，因此信息的传播是单方向的。BP网络是这类网络最典型的例子。

在相互结合型的网络中，任意神经元之间都可能有连接，因此，输入信号要在网络中往返传播，从某一初态开始，经过若干变化，渐渐趋于某一稳定状态或进入周期震荡等其他状态，这方面的网络有Hopfield网络、SOM网络等。

网络的学习能力体现在网络参数的调整上。参数调整方法为有教师学习和无教师学习两种基本方式。有教师学习方式是网络根据教师给出的正确输入模式，校正网络的参数，使其输出接近于正确模式。

这类方式常采用梯度下降的学习方法，如BP算法。而无教师学习是网络在没有教师直接指点下通过竞争等方式自动调整网络参数的学习方法，如自适应共振网络。神经网络就是由许多神经元互连在一起组成的神经结构。

把神经元之间相互作用的关系进行数学模型化就可以得到神经网络模型。目前已有几十种不同的神经网络模型。

代表的网络模型有感知器、反向传播BP网络、GMDH网络、RBF网络、双向联想记忆(BAM)、Hopfield网络、Boltsmann机、自适应共振网络(ART)、自组织特征映像(SOM)网络等。

运用这些网络模型可实现函数近似(数字逼近映像)、数据聚类、模式识别、优化计算等功能，因此，人工神经网络广泛用于人工智能、自动控制、机器人、统计学、工程学等领域的信息处理中。

(3)人工神经网络的结构A.神经元及其特性图7.16神经元模型人工神经网络的基本处理单元在神经网络中的作用与神经生理学中神经元的作用相似，因此，人工神经网络的基本处理单元往往被称为神经元。

人工神经网络结构中的神经元模型模拟一个生物神经元，如图7.16所示。该神经元单元由多个输入xi(i=1，2，…，n)和一个输出yj组成。

中间状态由输入信号的加权和与修正值表示，而输出为:煤层顶板稳定性评价、预测理论与方法式中:θj为神经元单元的偏置(阈值);wji为连接权系数(对于激发状态，wji取正值，对于抑制状态，wji取负值);n为输入信号数目;yj为神经元输出;t为时间;f()为输出变换函数，有时叫做激发或激励函数，往往采用0和1二值函数或S形函数，见图7.17，这3种函数都是连续和非线性的。

一种二值函数如图7.17(a)所示，可由下式表示:煤层顶板稳定性评价、预测理论与方法一种常规的S形函数如图7.17(b)所示，可由下式表示:煤层顶板稳定性评价、预测理论与方法常用双曲正切函数(如图7.17(c))来取代常规S形函数，因为S形函数的输出均为正值，而双曲正切函数的输出值可为正或负。

双曲正切函数如下式所示:图7.17神经元中的某些变换(激发)函数B.神经网络的基本类型1)人工神经网络的基本特性:人工神经网络由神经元模型构成，这种由许多神经元组成的信息处理网络具有并行分布结构。

每个神经元具有单一输出，并且能够与其他神经元连接;存在许多(多重)输出连接方法，每种连接方法对应一个连接权系数。

严格地说，人工神经网络是一种具有下列特性的有向图:①对于每个节点存在一个状态变量xi;②从节点i至节点j，存在一个连接权系数wji;③对于每个节点，存在一个阈值j;④对于每个节点，定义一个变换函数fj(xi，wji，j)，ij;对于最一般的情况，此函数取煤层顶板稳定性评价、预测理论与方法形式。

2)人工神经网络的主要学习算法:神经网络主要通过两种学习算法进行训练，即指导式(有师)学习算法和非指导式(无师)学习算法。此外，还存在第三种学习算法，即强化学习算法，可把它看做是有师学习的一种特例。

·有师学习:有师学习算法能够根据期望和实际的网络输出(对应于给定输入)间的差来调整神经元间连接的强度或权。因此，有师学习需要有个老师或导师来提供期望或目标输出信号。

·无师学习:无师学习算法不需要知道期望输出。在训练过程中，只要向神经网络提供输入模式，神经网络就能够自动地适应连接权，以便按相似特征把输入模式分组聚集。

无师学习算法的例子包括Kohonen算法和Carpenter-Grossberg自适应共振理论(ART)等。·强化学习:如前所述，强化学习是有师学习的特例。它不需要老师给出目标输出。

强化学习算法采用一个“评论员”来评价与给定输入相对应的神经网络输出的优度(质量因数)。强化学习算法的一个例子是遗传算法(GAs)。

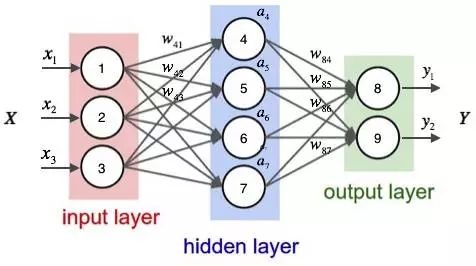
7.5.4.2多层前馈神经网络(BP)模型BP模型是目前研究最多、应用最广泛的ANN模型。它是由Rumelhart等组成的PDP小组于1985年提出的一种神经元模型，其结构如图7.18所示。

理论已经证明一个3层的BP网络模型能够实现任意的连续映像。

图7.18反向传播(BP)神经网络结构(1)BP网络模型特点BP(BackPropagation)网络模型是把一组样本的输入输出变成一个非线性优化问题，使用了最优化中最普遍的梯度下降算法，用迭代运算求解权，加入隐节点使得优化问题的可调参数增加，从而可以逼近精确解。

BP网络由输入层、输出层及隐含层组成，隐含层可有一个或多个，每层由多个神经元组成。其特点是:各层神经元仅与相邻层神经元之间有连接;各层内神经元之间无任何连接;各层神经元之间无反馈连接。

输入信号先向前传播到隐结点，经过变换函数之后，把隐结点的输出信息传播到输出结点，经过处理后再给出输出结果。结点的变换函数通常选取Sigmoid型函数。

一般情况下，隐含层采用S型对数或正切激活函数，而输出层采用线性激活函数。如果输入层有n个神经元，输出层有m个神经元，则网络是从n维欧氏空间到m维欧氏空间的映像。

在确定了BP网络的结构后，利用输入输出样本集对其进行训练，也即通过调整BP网络中的连接权值、网络的规模(包括n、m和隐层节点数)，就可以使网络实现给定的输入输出映像关系，并且可以以任意精度逼近任何非线性函数。

BP网络通过对简单的非线性函数的复合来完成映像，用这种方法经过少数的几次复合就可以得到极为复杂的函数关系，进而可以表达复杂的物理世界现象，使得许多实际问题都可以转为利用神经网络来解决。

经过训练的BP网络，对于不是样本集中的输入也能给出合适的输出，这种性质称为泛化(Generalization)功能。从函数拟合的角度看，这说明BP网络具有插值功能。

(2)BP网络学习算法BP神经网络采用误差反传学习算法，使用梯度搜索技术，实现网络的实际输出与期望输出的均方差最小化。网络学习的过程是一种边向后边传播边修正权的过程。

在这种网络中，学习过程由正向传播和反向传播组成。在正向过程中，输入信号从输入层经隐层单元逐层处理，并传向输出层，每一层神经元的状态只影响下一层神经元的状态。

如果在输出层不能得到期望的输出，则转向反向传播，将输出的误差按原来的连接通路返回。通过修改各层神经元的权值，使得误差信号最小。得到合适的网络连接值后，便可对新样本进行非线性映像。

A.信息的正向传递假设BP网络共L层，对于给定的P个样本，网络的期望输出为:煤层顶板稳定性评价、预测理论与方法当输入第P个样本时，对于网络中的第l(l=1，2，…，L-1)层中第j个神经元的操作特性为:煤层顶板稳定性评价、预测理论与方法式中:Wji———神经元i到神经元j的连接权值;nl-1———第l-1层的结点数;O(l-1)jp———神经元j的当前输入;O(l)jp———神经元j的输出;fl———非线性可微非递减函数，一般取为S型函数，即煤层顶板稳定性评价、预测理论与方法而对于输出层则有煤层顶板稳定性评价、预测理论与方法神经网络学习的目的是实现对每一样本煤层顶板稳定性评价、预测理论与方法，其中m为输出结点个数，达到最小，从而保证网络总误差极小化。

其中Tjdp，分别为输出层第j个节点的期望输出和实际输出。B.利用梯度下降法求权值变化及误差的反向传播采用梯度算法对网络权值、阈值进行修正。

第1层的权系数迭代方程为:煤层顶板稳定性评价、预测理论与方法式中:k———迭代次数。

令煤层顶板稳定性评价、预测理论与方法令煤层顶板稳定性评价、预测理论与方法，则有煤层顶板稳定性评价、预测理论与方法，其中，η为学习步长。

C.网络的训练过程1)网络初始化，用一组随机数对网络赋初始权值，设置学习步长η、允许误差ε、网络结构(即网络层数L和每层节点数nl);2)为网络提供一组学习样本;3)对每个学习样本p循环:a.逐层正向计算网络各节点的输入和输出;b.计算第p个样本的输出的误差Ep和网络的总误差E;c.当E小于允许误差ε或者达到指定的迭代次数时，学习过程结束，否则，进行误差反向传播，d.反向逐层计算网络各节点误差，如果fl取为S型函数，即，则对于输出层对于隐含层e.修正网络连接权值:煤层顶板稳定性评价、预测理论与方法式中:k———学习次数;η———学习因子。

η取值越大，每次权值的改变越剧烈，可能导致学习过程振荡，因此，为了使学习因子的取值足够大，又不致产生振荡，通常在权值修正公式中加入一个附加动量法。

表7.22指标定量化原则7.5.4.3基于多层前馈神经网络(BP)模型的煤层顶板评价思路由以上研究来看，BP人工神经网络模型是建立于已知因素的基础上，提取有关的权值等相关参数，然后去评价煤层顶板的稳定性。

因此，要想利用该方法对煤层顶板进行评价，应该通过以下几个思路:1)找出比较典型的能够反映某一井田的钻孔及能够反映顶板稳定性的资料，通过专家打分法或其他方法对其顶板稳定性进行评价;2)利用评价结果对不同等级的顶板稳定性进行分级定量的定义，并建立评价指标的定量化表，表7.22是对巨野煤田龙固井田进行分级的指标;3)通过已知并评价好的钻孔，代入到人工神经网络神经元公式进行大量的回算权值，并通过最终的分析确定出权值(Wkj)的值;4)将权值代入神经元模型，确定某一井田顶板稳定性模式，然后将井田内其他相关钻孔的地质资料带入，并得出其结果，代入表7.22进行分析得出井田钻孔周围顶板稳定性。

谷歌人工智能写作项目：爱发猫

人工神经网络的学习类型

学习是神经网络研究的一个重要内容，它的适应性是通过学习实现的写作猫。根据环境的变化，对权值进行调整，改善系统的行为。由Hebb提出的Hebb学习规则为神经网络的学习算法奠定了基础。

Hebb规则认为学习过程最终发生在神经元之间的突触部位，突触的联系强度随着突触前后神经元的活动而变化。在此基础上，人们提出了各种学习规则和算法，以适应不同网络模型的需要。

有效的学习算法，使得神经网络能够通过连接权值的调整，构造客观世界的内在表示，形成具有特色的信息处理方法，信息存储和处理体现在网络的连接中。

分类根据学习环境不同，神经网络的学习方式可分为监督学习和非监督学习。

在监督学习中，将训练样本的数据加到网络输入端，同时将相应的期望输出与网络输出相比较，得到误差信号，以此控制权值连接强度的调整，经多次训练后收敛到一个确定的权值。

当样本情况发生变化时，经学习可以修改权值以适应新的环境。使用监督学习的神经网络模型有反传网络、感知器等。非监督学习时，事先不给定标准样本，直接将网络置于环境之中，学习阶段与工作阶段成为一体。

此时，学习规律的变化服从连接权值的演变方程。非监督学习最简单的例子是Hebb学习规则。竞争学习规则是一个更复杂的非监督学习的例子，它是根据已建立的聚类进行权值调整。

自组织映射、适应谐振理论网络等都是与竞争学习有关的典型模型。

深度学习主要是学习哪些算法？

深度学习（也称为深度结构化学习或分层学习）是基于人工神经网络的更广泛的机器学习方法族的一部分。学习可以是有监督的、半监督的或无监督的。

深度学习架构，例如深度神经网络、深度信念网络、循环神经网络和卷积神经网络，已经被应用于包括计算机视觉、语音识别、自然语言处理、音频识别、社交网络过滤、机器翻译、生物信息学、药物设计、医学图像分析、材料检查和棋盘游戏程序在内的领域，在这些领域中，它们的成果可与人类专家媲美，并且在某些情况下胜过人类专家。

神经网络受到生物系统中信息处理和分布式通信节点的启发。人工神经网络与生物大脑有各种不同。具体而言，神经网络往往是静态和象征性的，而大多数生物的大脑是动态(可塑)和模拟的。

定义深度学习是一类机器学习算法：使用多个层逐步从原始输入中逐步提取更高级别的特征。例如，在图像处理中，较低层可以识别边缘，而较高层可以识别对人类有意义的部分，例如数字/字母或面部。

BP人工神经网络方法

（一）方法原理人工神经网络是由大量的类似人脑神经元的简单处理单元广泛地相互连接而成的复杂的网络系统。理论和实践表明，在信息处理方面，神经网络方法比传统模式识别方法更具有优势。

人工神经元是神经网络的基本处理单元，其接收的信息为x1，x2，…，xn，而ωij表示第i个神经元到第j个神经元的连接强度或称权重。

神经元的输入是接收信息X＝（x1，x2，…，xn）与权重W＝｛ωij｝的点积，将输入与设定的某一阈值作比较，再经过某种神经元激活函数f的作用，便得到该神经元的输出Oi。

常见的激活函数为Sigmoid型。

人工神经元的输入与输出的关系为地球物理勘探概论式中：xi为第i个输入元素，即n维输入矢量X的第i个分量；ωi为第i个输入与处理单元间的互联权重；θ为处理单元的内部阈值；y为处理单元的输出。

常用的人工神经网络是BP网络，它由输入层、隐含层和输出层三部分组成。BP算法是一种有监督的模式识别方法，包括学习和识别两部分，其中学习过程又可分为正向传播和反向传播两部分。

正向传播开始时，对所有的连接权值置随机数作为初值，选取模式集的任一模式作为输入，转向隐含层处理，并在输出层得到该模式对应的输出值。每一层神经元状态只影响下一层神经元状态。

此时，输出值一般与期望值存在较大的误差，需要通过误差反向传递过程，计算模式的各层神经元权值的变化量。这个过程不断重复，直至完成对该模式集所有模式的计算，产生这一轮训练值的变化量Δωij。

在修正网络中各种神经元的权值后，网络重新按照正向传播方式得到输出。实际输出值与期望值之间的误差可以导致新一轮的权值修正。正向传播与反向传播过程循环往复，直到网络收敛，得到网络收敛后的互联权值和阈值。

（二）BP神经网络计算步骤（1）初始化连接权值和阈值为一小的随机值，即W（0）＝任意值，θ（0）＝任意值。（2）输入一个样本X。

（3）正向传播，计算实际输出，即根据输入样本值、互联权值和阈值，计算样本的实际输出。

其中输入层的输出等于输入样本值，隐含层和输出层的输入为地球物理勘探概论输出为地球物理勘探概论式中：f为阈值逻辑函数，一般取Sigmoid函数，即地球物理勘探概论式中：θj表示阈值或偏置；θ0的作用是调节Sigmoid函数的形状。

较小的θ0将使Sigmoid函数逼近于阈值逻辑单元的特征，较大的θ0将导致Sigmoid函数变平缓，一般取θ0＝1。

（4）计算实际输出与理想输出的误差地球物理勘探概论式中：tpk为理想输出；Opk为实际输出；p为样本号；k为输出节点号。

（5）误差反向传播，修改权值地球物理勘探概论式中：地球物理勘探概论地球物理勘探概论（6）判断收敛。若误差小于给定值，则结束，否则转向步骤（2）。

（三）塔北雅克拉地区BP神经网络预测实例以塔北雅克拉地区S4井为已知样本，取氧化还原电位，放射性元素Rn、Th、Tc、U、K和地震反射构造面等7个特征为识别的依据。

构造面反映了局部构造的起伏变化，其局部隆起部位应是油气运移和富集的有利部位，它可以作为判断含油气性的诸种因素之一。

在该地区投入了高精度重磁、土壤微磁、频谱激电等多种方法，一些参数未入选为判别的特征参数，是因为某些参数是相关的。

在使用神经网络方法判别之前，还采用K-L变换（Karhaem-Loeve）来分析和提取特征。S4井位于测区西南部5线25点，是区内唯一已知井。

该井在5390.6m的侏罗系地层获得40.6m厚的油气层，在5482m深的震旦系地层中获58m厚的油气层。

取S4井周围9个点，即4～6线的23～25点作为已知油气的训练样本；由于区内没有未见油的钻井，只好根据地质资料分析，选取14～16线的55～57点作为非油气的训练样本。

BP网络学习迭代17174次，总误差为0.0001，学习效果相当满意。以学习后的网络进行识别，得出结果如图6-2-4所示。

图6-2-4塔北雅克拉地区BP神经网络聚类结果（据刘天佑等，1997）由图6-2-4可见，由预测值大于0.9可得5个大封闭圈远景区，其中测区南部①号远景区对应着已知油井S4井；②、③号油气远景区位于地震勘探所查明的托库1、2号构造，该两个构造位于沙雅隆起的东段，其西段即为1984年钻遇高产油气流的Sch2井，应是含油气性好的远景区；④、⑤号远景区位于大涝坝构造，是yh油田的组成部分。

人工神经网络是怎么学习的呢

1、神经网络的结构（例如2输入3隐节点1输出）建好后，一般就要求神经网络里的权值和阈值。现在一般求解权值和阈值，都是采用梯度下降之类的搜索算法（梯度下降法、牛顿法、列文伯格-马跨特法、狗腿法等等）。

2、这些算法会先初始化一个解，在这个解的基础上，确定一个搜索方向和一个移动步长（各种法算确定方向和步长的方法不同，也就使各种算法适用于解决不同的问题），使初始解根据这个方向和步长移动后，能使目标函数的输出（在神经网络中就是预测误差）下降。

3、然后将它更新为新的解，再继续寻找下一步的移动方向的步长，这样不断的迭代下去，目标函数（神经网络中的预测误差）也不断下降，最终就能找到一个解，使得目标函数（预测误差）比较小。

4、而在寻解过程中，步长太大，就会搜索得不仔细，可能跨过了优秀的解，而步长太小，又会使寻解过程进行得太慢。因此，步长设置适当非常重要。

5、学习率对原步长（在梯度下降法中就是梯度的长度）作调整，如果学习率lr=0.1,那么梯度下降法中每次调整的步长就是0.1*梯度，6、而在matlab神经网络工具箱里的lr,代表的是初始学习率。

因为matlab工具箱为了在寻解不同阶段更智能的选择合适的步长，使用的是可变学习率，它会根据上一次解的调整对目标函数带来的效果来对学习率作调整，再根据学习率决定步长。

神经网络算法的人工神经网络

人工神经网络（ArtificialNeuralNetworks，ANN）系统是20世纪40年代后出现的。

它是由众多的神经元可调的连接权值连接而成，具有大规模并行处理、分布式信息存储、良好的自组织自学习能力等特点。

BP（BackPropagation）算法又称为误差反向传播算法，是人工神经网络中的一种监督式的学习算法。

BP神经网络算法在理论上可以逼近任意函数，基本的结构由非线性变化单元组成，具有很强的非线性映射能力。

而且网络的中间层数、各层的处理单元数及网络的学习系数等参数可根据具体情况设定，灵活性很大，在优化、信号处理与模式识别、智能控制、故障诊断等许多领域都有着广泛的应用前景。

人工神经元的研究起源于脑神经元学说。19世纪末，在生物、生理学领域，Waldeger等人创建了神经元学说。人们认识到复杂的神经系统是由数目繁多的神经元组合而成。

大脑皮层包括有100亿个以上的神经元，每立方毫米约有数万个，它们互相联结形成神经网络，通过感觉器官和神经接受来自身体内外的各种信息，传递至中枢神经系统内，经过对信息的分析和综合，再通过运动神经发出控制信息，以此来实现机体与内外环境的联系，协调全身的各种机能活动。

神经元也和其他类型的细胞一样，包括有细胞膜、细胞质和细胞核。但是神经细胞的形态比较特殊，具有许多突起，因此又分为细胞体、轴突和树突三部分。细胞体内有细胞核，突起的作用是传递信息。

树突是作为引入输入信号的突起，而轴突是作为输出端的突起，它只有一个。树突是细胞体的延伸部分，它由细胞体发出后逐渐变细，全长各部位都可与其他神经元的轴突末梢相互联系，形成所谓“突触”。

在突触处两神经元并未连通，它只是发生信息传递功能的结合部，联系界面之间间隙约为（15～50)×10米。突触可分为兴奋性与抑制性两种类型，它相应于神经元之间耦合的极性。

每个神经元的突触数目正常，最高可达10个。各神经元之间的连接强度和极性有所不同，并且都可调整、基于这一特性，人脑具有存储信息的功能。利用大量神经元相互联接组成人工神经网络可显示出人的大脑的某些特征。

人工神经网络是由大量的简单基本元件——神经元相互联接而成的自适应非线性动态系统。每个神经元的结构和功能比较简单，但大量神经元组合产生的系统行为却非常复杂。

人工神经网络反映了人脑功能的若干基本特性，但并非生物系统的逼真描述，只是某种模仿、简化和抽象。

与数字计算机比较，人工神经网络在构成原理和功能特点等方面更加接近人脑，它不是按给定的程序一步一步地执行运算，而是能够自身适应环境、总结规律、完成某种运算、识别或过程控制。

人工神经网络首先要以一定的学习准则进行学习，然后才能工作。现以人工神经网络对于写“A”、“B”两个字母的识别为例进行说明，规定当“A”输入网络时，应该输出“1”，而当输入为“B”时，输出为“0”。

所以网络学习的准则应该是：如果网络作出错误的的判决，则通过网络的学习，应使得网络减少下次犯同样错误的可能性。

首先，给网络的各连接权值赋予(0，1)区间内的随机值，将“A”所对应的图象模式输入给网络，网络将输入模式加权求和、与门限比较、再进行非线性运算，得到网络的输出。

在此情况下，网络输出为“1”和“0”的概率各为50%，也就是说是完全随机的。这时如果输出为“1”(结果正确)，则使连接权值增大，以便使网络再次遇到“A”模式输入时，仍然能作出正确的判断。

如果输出为“0”(即结果错误)，则把网络连接权值朝着减小综合输入加权值的方向调整，其目的在于使网络下次再遇到“A”模式输入时，减小犯同样错误的可能性。

如此操作调整，当给网络轮番输入若干个手写字母“A”、“B”后，经过网络按以上学习方法进行若干次学习后，网络判断的正确率将大大提高。

这说明网络对这两个模式的学习已经获得了成功，它已将这两个模式分布地记忆在网络的各个连接权值上。当网络再次遇到其中任何一个模式时，能够作出迅速、准确的判断和识别。

一般说来，网络中所含的神经元个数越多，则它能记忆、识别的模式也就越多。（1）人类大脑有很强的自适应与自组织特性，后天的学习与训练可以开发许多各具特色的活动功能。

如盲人的听觉和触觉非常灵敏；聋哑人善于运用手势；训练有素的运动员可以表现出非凡的运动技巧等等。普通计算机的功能取决于程序中给出的知识和能力。显然，对于智能活动要通过总结编制程序将十分困难。

人工神经网络也具有初步的自适应与自组织能力。在学习或训练过程中改变突触权重值，以适应周围环境的要求。同一网络因学习方式及内容不同可具有不同的功能。

人工神经网络是一个具有学习能力的系统，可以发展知识，以致超过设计者原有的知识水平。

通常，它的学习训练方式可分为两种，一种是有监督或称有导师的学习，这时利用给定的样本标准进行分类或模仿；另一种是无监督学习或称无为导师学习，这时，只规定学习方式或某些规则，则具体的学习内容随系统所处环境（即输入信号情况）而异，系统可以自动发现环境特征和规律性，具有更近似人脑的功能。

（2）泛化能力泛化能力指对没有训练过的样本，有很好的预测能力和控制能力。特别是，当存在一些有噪声的样本，网络具备很好的预测能力。

(3)非线性映射能力当对系统对于设计人员来说，很透彻或者很清楚时，则一般利用数值分析，偏微分方程等数学工具建立精确的数学模型，但当对系统很复杂，或者系统未知，系统信息量很少时，建立精确的数学模型很困难时，神经网络的非线性映射能力则表现出优势，因为它不需要对系统进行透彻的了解，但是同时能达到输入与输出的映射关系，这就大大简化设计的难度。

(4)高度并行性并行性具有一定的争议性。承认具有并行性理由：神经网络是根据人的大脑而抽象出来的数学模型，由于人可以同时做一些事，所以从功能的模拟角度上看，神经网络也应具备很强的并行性。

多少年以来，人们从医学、生物学、生理学、哲学、信息学、计算机科学、认知学、组织协同学等各个角度企图认识并解答上述问题。

在寻找上述问题答案的研究过程中，这些年来逐渐形成了一个新兴的多学科交叉技术领域，称之为“神经网络”。神经网络的研究涉及众多学科领域，这些领域互相结合、相互渗透并相互推动。

不同领域的科学家又从各自学科的兴趣与特色出发，提出不同的问题，从不同的角度进行研究。

下面将人工神经网络与通用的计算机工作特点来对比一下：若从速度的角度出发，人脑神经元之间传递信息的速度要远低于计算机，前者为毫秒量级，而后者的频率往往可达几百兆赫。

但是，由于人脑是一个大规模并行与串行组合处理系统，因而，在许多问题上可以作出快速判断、决策和处理，其速度则远高于串行结构的普通计算机。

人工神经网络的基本结构模仿人脑，具有并行处理特征，可以大大提高工作速度。人脑存贮信息的特点为利用突触效能的变化来调整存贮内容，也即信息存贮在神经元之间连接强度的分布上，存贮区与计算机区合为一体。

虽然人脑每日有大量神经细胞死亡（平均每小时约一千个），但不影响大脑的正常思维活动。

普通计算机是具有相互独立的存贮器和运算器，知识存贮与数据运算互不相关，只有通过人编出的程序使之沟通，这种沟通不能超越程序编制者的预想。元器件的局部损坏及程序中的微小错误都可能引起严重的失常。

心理学家和认知科学家研究神经网络的目的在于探索人脑加工、储存和搜索信息的机制，弄清人脑功能的机理，建立人类认知过程的微结构理论。

生物学、医学、脑科学专家试图通过神经网络的研究推动脑科学向定量、精确和理论化体系发展，同时也寄希望于临床医学的新突破；信息处理和计算机科学家研究这一问题的目的在于寻求新的途径以解决不能解决或解决起来有极大困难的大量问题，构造更加逼近人脑功能的新一代计算机。

人工神经网络早期的研究工作应追溯至上世纪40年代。下面以时间顺序，以著名的人物或某一方面突出的研究成果为线索，简要介绍人工神经网络的发展历史。

1943年，心理学家W·Mcculloch和数理逻辑学家W·Pitts在分析、总结神经元基本特性的基础上首先提出神经元的数学模型。此模型沿用至今，并且直接影响着这一领域研究的进展。

因而，他们两人可称为人工神经网络研究的先驱。1945年冯·诺依曼领导的设计小组试制成功存储程序式电子计算机，标志着电子计算机时代的开始。

1948年，他在研究工作中比较了人脑结构与存储程序式计算机的根本区别，提出了以简单神经元构成的再生自动机网络结构。

但是，由于指令存储式计算机技术的发展非常迅速，迫使他放弃了神经网络研究的新途径，继续投身于指令存储式计算机技术的研究，并在此领域作出了巨大贡献。

虽然，冯·诺依曼的名字是与普通计算机联系在一起的，但他也是人工神经网络研究的先驱之一。50年代末，F·Rosenblatt设计制作了“感知机”，它是一种多层的神经网络。

这项工作首次把人工神经网络的研究从理论探讨付诸工程实践。当时，世界上许多实验室仿效制作感知机，分别应用于文字识别、声音识别、声纳信号识别以及学习记忆问题的研究。

然而，这次人工神经网络的研究高潮未能持续很久，许多人陆续放弃了这方面的研究工作，这是因为当时数字计算机的发展处于全盛时期，许多人误以为数字计算机可以解决人工智能、模式识别、专家系统等方面的一切问题，使感知机的工作得不到重视；其次，当时的电子技术工艺水平比较落后，主要的元件是电子管或晶体管，利用它们制作的神经网络体积庞大，价格昂贵，要制作在规模上与真实的神经网络相似是完全不可能的；另外，在1968年一本名为《感知机》的著作中指出线性感知机功能是有限的，它不能解决如异感这样的基本问题，而且多层网络还不能找到有效的计算方法，这些论点促使大批研究人员对于人工神经网络的前景失去信心。

60年代末期，人工神经网络的研究进入了低潮。另外，在60年代初期，Widrow提出了自适应线性元件网络，这是一种连续取值的线性加权求和阈值网络。后来，在此基础上发展了非线性多层自适应网络。

当时，这些工作虽未标出神经网络的名称，而实际上就是一种人工神经网络模型。随着人们对感知机兴趣的衰退，神经网络的研究沉寂了相当长的时间。

80年代初期，模拟与数字混合的超大规模集成电路制作技术提高到新的水平，完全付诸实用化，此外，数字计算机的发展在若干应用领域遇到困难。这一背景预示，向人工神经网络寻求出路的时机已经成熟。

美国的物理学家Hopfield于1982年和1984年在美国科学院院刊上发表了两篇关于人工神经网络研究的论文，引起了巨大的反响。人们重新认识到神经网络的威力以及付诸应用的现实性。

随即，一大批学者和研究人员围绕着Hopfield提出的方法展开了进一步的工作，形成了80年代中期以来人工神经网络的研究热潮。

1985年，Ackley、Hinton和Sejnowski将模拟退火算法应用到神经网络训练中，提出了Boltzmann机，该算法具有逃离极值的优点，但是训练时间需要很长。

1986年，Rumelhart、Hinton和Williams提出了多层前馈神经网络的学习算法，即BP算法。它从证明的角度推导算法的正确性，是学习算法有理论依据。从学习算法角度上看，是一个很大的进步。

1988年，Broomhead和Lowe第一次提出了径向基网络：RBF网络。总体来说，神经网络经历了从高潮到低谷，再到高潮的阶段，充满曲折的过程。

　人工神经网络分类方法

从20世纪80年代末期，人工神经网络方法开始应用于遥感图像的自动分类。

目前，在遥感图像的自动分类方面，应用和研究比较多的人工神经网络方法主要有以下几种：（1）BP（BackPropagation）神经网络，这是一种应用较广泛的前馈式网络，属于有监督分类算法，它将先验知识融于网络学习之中，加以最大限度地利用，适应性好，在类别数少的情况下能够得到相当高的精度，但是其网络的学习主要采用误差修正算法，识别对象种类多时，随着网络规模的扩大，需要的计算过程较长，收敛缓慢而不稳定，且识别精度难以达到要求。

（2）Hopfield神经网络。属于反馈式网络。主要采用Hebb规则进行学习，一般情况下计算的收敛速度较快。

这种网络是美国物理学家J.J.Hopfield于1982年首先提出的，它主要用于模拟生物神经网络的记忆机理。

Hopfield神经网络状态的演变过程是一个非线性动力学系统，可以用一组非线性差分方程来描述。

系统的稳定性可用所谓的“能量函数”进行分析，在满足一定条件下，某种“能量函数”的能量在网络运行过程中不断地减少，最后趋于稳定的平衡状态。

Hopfield网络的演变过程是一种计算联想记忆或求解优化问题的过程。（3）Kohonen网络。

这是一种由芬兰赫尔辛基大学神经网络专家Kohonen（1981）提出的自组织神经网络，其采用了无导师信息的学习算法，这种学习算法仅根据输入数据的属性而调整权值，进而完成向环境学习、自动分类和聚类等任务。

其最大的优点是最终的各个相邻聚类之间是有相似关系的，即使识别时把样本映射到了一个错误的节点，它也倾向于被识别成同一个因素或者一个相近的因素，这就十分接近人的识别特性。