台湾地区信用卡客户贷款违约预测

数据集地址：
链接：https://pan.baidu.com/s/1vQgkQs1aTC-zm6zcDH4kKQ
提取码：6ois

1 数据说明与导入

导入必需的库和数据。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline

import sklearn
from sklearn.model_selection import train_test_split # 分离数据集和测试集
from sklearn.neighbors import KNeighborsClassifier 
from sklearn import metrics # 一些评价指标
from sklearn.metrics import precision_recall_curve # 召回率
from sklearn.metrics import confusion_matrix # 混淆矩阵
from sklearn import preprocessing
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

df = pd.read_csv('./UCI_Credit_Card.csv') # 导入数据
1

2 数据初步探索

2.1 数据信息检查

df.head()
1

df.shape
df.info()
df.describe()
1
2
3

一共有30000名信用卡持卡人的信息，这些持卡人信用卡平均额度LIMIT_BAL为167484，但是标准差达到了129747，信用卡最大额度达到100万新台币，额度最小的仅有10000新台币，跨度非常大；我们已知2代表女性，1代表男性，性别SEX的平均值在1.6以上，说明女性在该样本中的占比明显高于男性。同时我们也发现与描述不符的异常数据，教育程度EDUCATION的最大值和最小值均在给定的字段描述之外，婚姻状况MARRIAGE有标记为3的点，PAY_1到PAY_6的还款记录中出现了描述之外的-2，我们应逐一进行理解与清洗。

2.2 数据清洗

首先，查看教育程度。

df['EDUCATION'].value_counts()
1

2 14030
1 10585
3 4917
5 280
4 123
6 51
0 14
Name: EDUCATION, dtype: int64

教育程度标记为4,5,6的值都可以理解为“其他”，代表低于高中的学历。为了将学历按低到高进行排序，交换了标签1和标签3。

df['EDUCATION'].replace([1,3,4,5,6],[3,1,0,0,0],inplace=True)
df['EDUCATION'].value_counts()
1
2

2 14030
3 10585
1 4917
0 468
Name: EDUCATION, dtype: int64

将性别SEX数据中男性和女性标记为0和1，符合编程习惯。

df['SEX'].replace([1,2],[0,1],inplace=True)
df['SEX'].value_counts()
1
2

1 18112
0 11888
Name: SEX, dtype: int64

df['MARRIAGE'].value_counts()
1

2 15964
1 13659
3 323
0 54
Name: MARRIAGE, dtype: int64

df['MARRIAGE'].replace(3,0,inplace=True)
df['MARRIAGE'].value_counts()
1
2

2 15964
1 13659
0 377
Name: MARRIAGE, dtype: int64

最后，我们对标记还款状况的列 PAY_1 到PAY_6 也同样进行查看。首先取 PAY_1 一列为例子。

df['PAY_1'].value_counts()
1

0 14737
-1 5686
1 3688
-2 2759
2 2667
3 322
4 76
5 26
8 19
6 11
7 9
Name: PAY_1, dtype: int64

还款为-2，-1，0均应视为还清债务，我们将其统一标记为0。经过验证PAY_1到PAY_6的数据具有同样特征，我们用iloc定位我们要替换的列，进行替换操作。

df.iloc[:,[6,7,8,9,10,11]] = df.iloc[:,[6,7,8,9,10,11]].replace([-1,-2],[0,0])
df.iloc[:,[6,7,8,9,10,11]].describe()
1
2

df['default.payment.next.month'].value_counts()[0]/df['default.payment.next.month'].value_counts()[1]
1

正负样本的比例大概是3.5:1，数据存在不平衡问题。

2.3 数据可视化与分析

2.3.1 数据分布情况

plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
sns.set(rc={'figure.figsize':(10,5),"font.size":15,'font.sans-serif':['SimHei'],"axes.titlesize":15,"axes.labelsize":15})
plt.title('信用额度分布图')
# 改变 matplotlib 颜色缩写词的解释方式
sns.set_color_codes("pastel")
# kde：是否绘制高斯核密度估计图 bins：直方图bins(柱)的数目
sns.distplot(df['LIMIT_BAL'],kde=True,bins=200, color="blue")
plt.xlabel("信用额度")

plt.rcParams['figure.dpi'] = 1200 #为了使图片更加清晰
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

可以看到信用额度的分布很不均匀，少数人群的信用额度非常高，大部分人的信用额度集中在较低的值。

sns.set(rc={'figure.figsize':(10,5),"font.size":15,'font.sans-serif':['SimHei'],"axes.titlesize":15,"axes.labelsize":15})
#
sns.set_color_codes("pastel")
sns.displot(df['AGE'],kde=True,bins=59, color="green")
plt.xlabel("年龄")
plt.title('客户年龄分布图')
plt.show()
1
2
3
4
5
6
7

从图中能够发现，客户的年龄主要集中在20-40岁之间。

对于离散型变量SEX、EDUCATION，MARRIAGE，使用饼图查看数据的占比情况。

# 绘制多个子图，1行3列
fig = plt.subplots(3,figsize=(16,12))
sns.set(rc={'figure.figsize':(10,5),"font.size":15,'font.sans-serif':['SimHei'],"axes.titlesize":15,"axes.labelsize":15})

# 绘制第一个子图
plt.subplot(1,3,1)
sex_count = df['SEX'].value_counts()
# 画饼图，设置扇形标签，设置百分比显示格式，一位小数百分比
sex_count.plot(kind='pie', labels=['女性','男性'], autopct='%1.1f%%')
plt.ylabel("")
plt.title('性别分布图')

plt.subplot(1,3,2)
edu_count = df['EDUCATION'].value_counts()
edu_count.plot(kind='pie', labels=['本科', '研究生或以上','高中','其他'], autopct='%1.1f%%')
plt.title('教育情况分布图')
plt.ylabel("")

plt.subplot(1,3,3)
mar_count = df['MARRIAGE'].value_counts()
mar_count.plot(kind='pie', labels=['未婚', '已婚','其他'], autopct='%1.1f%%')
plt.title('婚姻状况分布图')
plt.ylabel("")

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

从本图中可以看出性别的分布不均匀，女性占比显著高于男性。教育情况上，72%的客户教育程度都在本科或以上。婚姻状况则显示已婚和未婚客户的数目差距不多。

2.3.2 结合违约情况查看数据分布

考察对于不同的性别，年龄和教育情况，客户的违约情况是否有着比较显著的区别。

sns.set(rc={'figure.figsize':(13,5),"font.size":15,'font.sans-serif':['SimHei'],"axes.titlesize":15,"axes.labelsize":15})
plt.figure()
# fig代表绘图窗口(Figure)；ax代表这个绘图窗口上的坐标系(axis)
fig, ax = plt.subplots(1,3,figsize=(12,5))

plt.subplot(1,3,1)
# 条形图，以x轴标签划分统计个数，再以hue标签统计违约与未违约的个数
ax=sns.countplot(x='SEX',hue='default.payment.next.month',data = df)
# 设置x轴不同标签名称
ax.set_xticklabels(['男', '女'],fontsize=12)
# 设置x轴名称
plt.xlabel("性别")
plt.ylabel("")
# 设置图的标题
plt.title('不同性别违约情况')

plt.subplot(1,3,2)
ax=sns.countplot(x='EDUCATION',hue='default.payment.next.month',data = df)
ax.set_xticklabels(['其他', '高中','本科','研究生及以上'],fontsize=12)
plt.xlabel("教育程度")
plt.ylabel("")
plt.title('不同教育程度违约情况')


plt.subplot(1,3,3)
ax=sns.countplot(x='MARRIAGE',hue='default.payment.next.month',data = df)
ax.set_xticklabels(['其他', '已婚','未婚'], fontsize=12)
plt.xlabel("婚姻状况")
plt.ylabel("")
plt.title('不同婚姻状况违约情况')

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

从图中可以看出，虽然男性的数量远低于女性，但违约人数并没有明显低于女性违约人数。对于婚姻状况也存在类似情况，未婚的人数比已婚人数多，但违约人数和已婚的违约人数相差无几，也说明了未婚人数的违约概率可能要大一些。

我们再考察对于年龄和信用卡额度的违约情况。

t0 = df[df['default.payment.next.month'] == 0]   # 未违约的样本数据
t1 = df[df['default.payment.next.month'] == 1]   # 违约的样本数据
plt.figure()
fig, ax = plt.subplots(1,2,figsize=(12,6))

# 画第一个子图
plt.subplot(1,2,1)
# 画直方图，设置高斯核密度估计图参数，以字典传入核密度图的属性信息
sns.distplot(t0['AGE'],kde_kws={"color":"blue","label":"未违约"})
sns.distplot(t1['AGE'],kde_kws={"color":"orange","label":"违约"})
# 设置x轴名称、字符大小
plt.xlabel('年龄', fontsize=12)
locs, labels = plt.xticks()
plt.title('不同年龄违约情况')
# 刻度线参数设置
plt.tick_params(axis='both', which='major', labelsize=12)

plt.subplot(1,2,2)
sns.distplot(t0["LIMIT_BAL"],kde_kws={"color":"blue","label":"未违约"})
sns.distplot(t1["LIMIT_BAL"],kde_kws={"color":"orange","label":"违约"})
plt.xlabel('信用卡额度', fontsize=12)
locs, labels = plt.xticks()
plt.title('不同信用卡额度违约情况')
plt.tick_params(axis='both', which='major', labelsize=12)

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

仔细观察上图，我们可以获取更多有趣的信息。例如30岁前，客户的违约概率更大；30-40岁之间是客户信用最高的区间，40岁之后再次下降；信用卡额度较低的客户违约概率更高。

3 分类建模

我们首先尝试使用一些基本的机器学习模型对数据直接进行分类建模，并给出分类的预测结果。我们选用比较经典的KNN和决策树来观察效果。

3.1 KNN模型

在KNN模型中，由于要计算欧氏距离，因此应该先对离散变量做哑变量编码处理，使其变为数值型特征
我们对无序离散变量SEX,MARRIAGE进行哑变量编码。

str_columns = ['SEX','MARRIAGE']
df_new = pd.get_dummies(df, columns=str_columns)
1
2

y = df_new['default.payment.next.month']  #因变量
X = df_new.drop(columns=['ID','default.payment.next.month']) #去除因变量与ID，剩余为特征
1
2

数值型的变量的各指标相差很大时，如果直接使用原始值计算，就会突出数值较大的指标在分析中的作用、削弱数值较小的指标在分析中的作用，所以要进行特征缩放。

对特征列进行标准化处理，使得处理过后的每一列数据都是均值为0，标准差为1的数据。

X.iloc[:,0:21] = preprocessing.scale(X.iloc[:,0:21])
1

划分数据集。

X_train, X_test,y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
1

下面，我们使用sklearn中的KNeighborsClassifier对训练集进行分类训练。当不输入参数时，默认KNN所选取的n_neighbors参数取值为5。

# 创建knn类
knn_model = KNeighborsClassifier()
# 对数据进行拟合学习
knn_model.fit(X_train, y_train)
1
2
3
4

得到模型knn_model后，我们在测试集上验证其分类效果
用predict方法获取模型对每一个测试集样本标签的预测结果knn_pred
用predict_proba方法获取模型把每一个样本划分为正类的概率knn_score

# 预测结果
knn_pred = knn_model.predict(X_test)
# 属于正类的概率
knn_score = knn_model.predict_proba(X_test)[:,1]
1
2
3
4

为了展示分类模型的效果，我们需要获取模型的准确率得分，分类报告以及混淆矩阵。
sklearn中的accuracy_score用于计算准确率
sklearn中的classification_report函数用于显示主要分类指标的文本报告．在报告中显示每个类的精确度，召回率，F1值等信息
sklearn中的confusion_matrix总结模型真实值与预测值的情形分析表，以矩阵形式显示

为了方便后续使用，我们定义一个函数Get_report来获取这些信息。

Get_report(y_test , knn_pred)
1

模型的准确率为：0.7915555555555556
模型的分类报告展示如下:
precision recall f1-score support

       0       0.84      0.91      0.87      7060
       1       0.53      0.35      0.42      1940

accuracy                           0.79      9000
1
2
3
4

macro avg 0.68 0.63 0.64 9000
weighted avg 0.77 0.79 0.77 9000

模型的混淆矩阵展示如下:
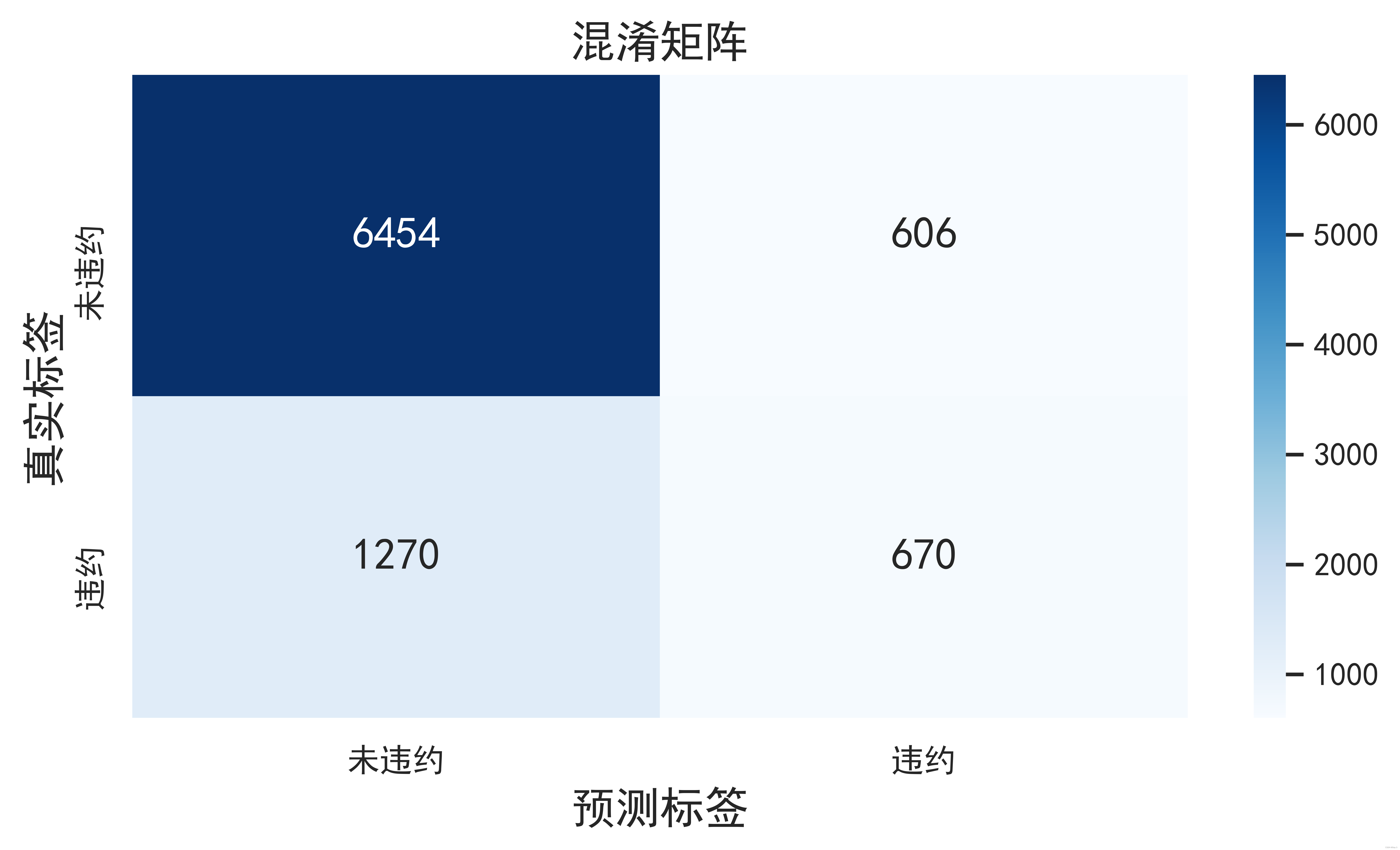
我们发现，虽然总体预测的精准度尚可，违约样本的实际召回率只有0.27，能够综合展示正类样本的准确率和召回率的f1-score只有0.36。我们再尝试其他模型进行对比。

3.2 决策树

引入决策树算法，直接进行模型训练，并展示模型训练结果，与KNN得到的结果进行对比。

from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
tree_model = DecisionTreeClassifier(random_state=1)
tree_model.fit(X_train, y_train)
1
2
3
4

tree_score = tree_model.predict_proba(X_test)[:,1]
tree_pred = tree_model.predict(X_test)
Get_report(y_test,tree_pred)
1
2
3

模型的准确率为：0.7307777777777777
模型的分类报告展示如下:
precision recall f1-score support

       0       0.84      0.82      0.83      7060
       1       0.39      0.42      0.40      1940

accuracy                           0.73      9000
1
2
3
4

macro avg 0.61 0.62 0.61 9000
weighted avg 0.74 0.73 0.74 9000

模型的混淆矩阵展示如下:

4 数据过采样

在使用KNN算法和决策树算法后，我们得到的训练结果均较为一般，我们重新回顾之前得到的结论：这个样本是一个存在类别不平衡问题的样本。

from imblearn.over_sampling import SMOTE
# 划分数据集
X_train, X_test,\
y_train, y_test \
= train_test_split(X, y, test_size=0.3, random_state=0)
# 定义一个SMOTE模型
smo = SMOTE(random_state=42)
# fit_resample拟合数据
X_smo, y_smo = smo.fit_resample(X_train, y_train)
1
2
3
4
5
6
7
8
9

from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
tree_model = DecisionTreeClassifier(random_state=1)
tree_model.fit(X_smo, y_smo)
1
2
3
4

tree_score = tree_model.predict_proba(X_test)[:,1]
tree_pred = tree_model.predict(X_test)
Get_report(y_test,tree_pred)
1
2
3

5 引入新评价指标

同时，针对不平衡样本的评价指标也需要进行相应的更新，我们可以引入Precision_Recall_curve、AP值、ROC_curve、G-mean

我们定一个Get_curve函数，展示这些曲线，并给出一系列对应的数值。

6 集成学习

下面我们引入一种强力的算法-XGBoost，作为Boosting的代表之一，它是对GBDT(Gradient Boosting Decision Tree)的一种改进，我们在对数据进行重采样后进行学习。

6.1 XGBoost

# 划分数据集
X_train, X_test,\
y_train, y_test \
= train_test_split(X, y, test_size=0.3, random_state=0)

# 过采样处理
smo = SMOTE(random_state=42)
X_smo, y_smo = smo.fit_resample(X_train, y_train)
1
2
3
4
5
6
7
8

from xgboost import XGBClassifier
model = XGBClassifier(booster='gbtree',learning_rate=0.1,gamma=1,scale_pos_weight=1,n_estimators=1000,max_depth=6,alpha=5,reg_lambda=1)
# 设置训练数据
eval_set = [(X_test, y_test)]
model.fit(X_smo, y_smo, early_stopping_rounds=10, eval_metric="auc", eval_set=eval_set, verbose=False)
1
2
3
4
5

y_pred = model.predict(X_test)
y_socre = model.predict_proba(X_test)[:,1]
# predictions = [round(value) for value in y_pred]
1
2
3

Get_curve(y_test,y_socre,y_pred)
1

AP值:0.5284780662232265
F1最大对应阈值 = 0.49564602971076965
Gmean最大对应阈值 = 0.4803217351436615
准确率得分= 0.7938888888888889
最大Gmean = 0.7028493826938129
最大F1 = 0.5300546448087432

6.2 CATBOOST

我们最后再使用一种在处理类别特征时通常效果更好的算法:CatBoost。它的基本原理类似于常规的Gradient Boosting算法，它一方面可以自动处理分类特征

由于可以自动处理分类特征，我们可以直接使用未进行哑变量编码的数据进行计算。

y = df['default.payment.next.month'] # 因变量
X = df.drop(columns=['ID','default.payment.next.month']) # 去除ID与因变量，剩余为特征
X_train, X_test,\
y_train, y_test \
= train_test_split(X, y, test_size=0.3, random_state=0)
1
2
3
4
5

from sklearn.model_selection import GridSearchCV
from catboost import CatBoostClassifier

categorical_features_indices = ['SEX','MARRIAGE']
model = CatBoostClassifier(iterations=100, depth=6, cat_features = categorical_features_indices, loss_function='Logloss', logging_level='Silent')
model.fit(X_train,y_train,eval_set=(X_test, y_test))
1
2
3
4
5
6

cb_pred = model.predict(X_test)
cb_socre = model.predict_proba(X_test)[:,1]
# predictions = [round(value) for value in cb_pred]
1
2
3

Get_curve(y_test, cb_socre, cb_pred)
1

AP值:0.5496398051016296
F1最大对应阈值 = 0.2518803714670295
Gmean最大对应阈值 = 0.21489477235998308
准确率得分= 0.8255555555555556
最大Gmean = 0.7112365138132554
最大F1 = 0.5477949940405245

综合来看，CatBoost取得了较好的效果，但我们发现G-mean的最大值和F1的最大值并不能同时取到，二者之间存在取舍关系，在处理实际问题时，需要根据对正类样本的分类需求来决定。是更加追求正类样本的召回率，还是整体判别的精确性？此处我们分别给出G-mean最大时的模型和F1最大时的模型，仅供参考。

THRESHOLD = 0.2518803714670295
# 大于阈值输出1，小于则输出0
y_pred = np.where(model.predict_proba(X_test)[:,1] >= THRESHOLD, 1, 0)
Get_report(y_test,y_pred)
1
2
3
4

模型的准确率为：0.7892222222222223
模型的分类报告展示如下:
precision recall f1-score support

       0       0.88      0.84      0.86      7060
       1       0.51      0.59      0.55      1940

accuracy                           0.79      9000
1
2
3
4

macro avg 0.70 0.72 0.71 9000
weighted avg 0.80 0.79 0.79 9000
这是追求F1最大时的效果，此时设置分类阈值为0.2518803714670295 ， F1值达到了0.55。

THRESHOLD = 0.21489477235998308
# 大于阈值输出1，小于则输出0
y_pred = np.where(model.predict_proba(X_test)[:,1] >= THRESHOLD, 1, 0)
Get_report(y_test,y_pred)
1
2
3
4

模型的准确率为：0.7566666666666667
模型的分类报告展示如下:
precision recall f1-score support

       0       0.89      0.79      0.84      7060
       1       0.45      0.64      0.53      1940

accuracy                           0.76      9000
1
2
3
4

macro avg 0.67 0.71 0.68 9000
weighted avg 0.80 0.76 0.77 9000

这是追求Gmeans最大时的效果，此时设置分类阈值为0.21489477235998308，F1值有一定的下降，但是正类样本的召回率达到了0.64。根据实际问题的不同需求，两种结果具有不同的实际意义。例如，如果我们认为放过违约样本的代价较大，我们可以选择以Gmeans最大化作为算法的评价指标。

7 结论

对于不平衡样本的分类问题，直接使用机器学习模型并非能得到很好的效果，重采样是可能能够提升模型训练效果的办法。本案例一共使用了六种不同的分类模型算法，其中CatBoost实现了最好的分类效果。