-
神经网络(六)循环神经网络
一、增加记忆功能
1.可计算问题

其中函数不涉及记忆问题,可以使用前馈神经网络计算
但是图灵机涉及记忆问题,需要为神经网络增加记忆能力
2.如何增加记忆能力
①时延神经网络
额外增加一个延时单元(用以存储网络的历史信息<输入、输出、隐状态等>)

②自回归模型
用变量yt的历史信息来预测自己

③有外部输入的非线性自回归模型

f(.)为非线性函数,可以是前馈网络。Kx和Ky为超参数

二、循环神经网络
循环神经网络的神经元自带反馈,可以处理任意长度的时序数据。

循环神经网络比前馈神经网络更符合神生物经网络的结构,被广泛应用在语音设备、预言模型、及自然语言生成等任务。
将循环神经网络按时间展开

其在时间维上极深,同样存在梯度消失问题。在非时间维上较浅,需要适度增加其模型复杂度。
1.简单循环神经网络

一个完全连接的循环网络是任何非线性动力系统的近似器。
循环神经网络通用近似定理


St为每个时刻的隐藏状态,xt为外部输入,g(.)为状态转换函数,O(.)为连续输出函数
图灵完备
可以实现图灵机的所用功能(可以解决所有可以算问题),一个完全连接的循环神经网络可以近似于图灵完备
2.应用到机器学习
①序列到类别

将所有h进行平均/求和,再送入分类器之中
②同步的序列到序列模式

例如:中文分词、信息抽取(文本中抽取信息,形成知识)、语音识别--等容易出现分歧的问题
③异步的序列到序列模式

例如:机器翻译
3.参数学习与长程依赖问题
①参数学习
以同步的序列到序列循环神经网络为例,给定一个学习样本(x,y),长度均为T

时刻t的瞬时损失函数为:

 为后验概率
为后验概率总损失函数:

计算梯度:



 为第t时刻的损失对第k步隐藏神经元的净输入
为第t时刻的损失对第k步隐藏神经元的净输入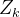 的导数
的导数
tips:diag(x,n):矩阵x上的第n条对角线上的元素

随时间的反向传播算法(BPTT)



②长程依赖问题
当
 且
且 ,
, 时会出现梯度爆炸问题
时会出现梯度爆炸问题当
 且
且 ,
, 时会出现梯度消失问题
时会出现梯度消失问题梯度爆炸和梯度消失统称为长程依赖问题,由于此问题,实际上只能学习到短周期的依赖关系。
原因是循环神经网络在时间维度上非常深
1.修正梯度爆炸问题
权重衰减、梯度截断
2.修正梯度消失问题
改进模型,使
 与
与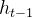 之间的线性关系移动到
之间的线性关系移动到 上
上改进方法①:令梯度

将循环边改为线性依赖关系:
 会削弱非线性性能
会削弱非线性性能其中

增加非线性:

其中

4.常见的循环神经网络
门控机制:控制信息积累的速度。(选择性的加入新的信息,选择性遗忘)
①GRU(门控循环单元)

更新门
 ,值域为[0,1],用于选择性遗忘。
,值域为[0,1],用于选择性遗忘。
 ,使用tanh实现
,使用tanh实现
改进
 ,使
,使 仅与
仅与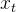 相关(去除与
相关(去除与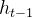 的联系)
的联系)重置门
 ,
,
 ,
,
门控循环单元

②LSTM(长短期记忆网络)

引入内部记忆单元
 用于记忆,解放
用于记忆,解放 ,使其可以更好的进行非线性拟合
,使其可以更好的进行非线性拟合


!!! 可以使得

各种变体

5.深层循环神经网络
①堆叠循环神经网络

②双向循环神经网络

三、小结
优点:引入记忆功能、图灵完备
缺点:长程依赖问题、记忆容量问题、并行能力问题
四、将循环神经网络扩展到图
序列是最简单的数据结构,更复杂的结构还有树和图
1.递归神经网络
用于处理树结构。

在一个有向无循环图共享一个组合函数
2.图网络
用于处理图结构。

更新序列:先更新点、再更新边、最后更新全局结点

对于任意图结构G(V,E)
更新函数:


读出函数:

-
相关阅读:
小程序面试题七
IPKISS Tutorials ------merge elements(合并对象)
Cobalt Strike-修改默认证书、混淆流量-教程
2004NOIP普及组真题 2. 花生采摘
【C语言】模拟实现strlen
salesforce零基础学习(一百一十七)salesforce部署方式及适用场景
计算机毕业设计之java+javaweb的校园音乐平台
基于java的医院微信小程序
CMake教程-第 1 步:基本起点
图形学 - 纹理映射与重心坐标
- 原文地址:https://blog.csdn.net/weixin_37878740/article/details/126460644