【655. 输出二叉树】

来源：力扣（LeetCode）

描述：

给你一棵二叉树的根节点 root ，请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ，用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则：

• 树的 高度 为 height ，矩阵的行数 m 应该等于 height + 1 。

• 矩阵的列数 n 应该等于 2^height+1 - 1 。

• 根节点 需要放置在 顶行 的 正中间 ，对应位置为 res[0][(n - 1) / 2] 。

• 对于放置在矩阵中的每个节点，设对应位置为 res[r][c] ，将其左子节点放置在 res[r + 1][c - 2^height-r-1] ，右子节点放置在 res[r + 1][c + 2^height-r-1] 。

• 继续这一过程，直到树中的所有节点都妥善放置。

• 任意空单元格都应该包含空字符串 "" 。

返回构造得到的矩阵 res 。

示例 1：

输入：root = [1,2]
输出：
[["","1",""],
 ["2","",""]]
1
2
3
4

示例 2：

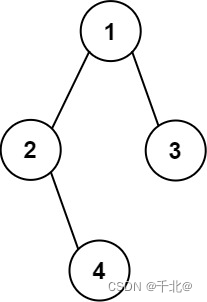
输入：root = [1,2,3,null,4]
输出：
[["","","","1","","",""],
 ["","2","","","","3",""],
 ["","","4","","","",""]]
1
2
3
4
5

提示：

• 树中节点数在范围 [1, 2¹⁰] 内

• -99 <= Node.val <= 99

• 树的深度在范围 [1, 10] 内

方法一：深度优先搜索

思路与算法

我们可以通过深度优先搜索来解决此题。首先通过深度优先搜索来得到二叉树的高度 height（注意高度从 0 开始），然后创建一个行数为 m = height + 1，列数为 n = 2 ^height+1 −1 的答案数组 res 放置节点的值（字符串形式）。根节点的值应当放在当前空间的第一行正中间。根节点所在的行与列会将剩余空间划分为两部分（左下部分和右下部分），然后递归地将左子树输出在左下部分空间，右子树输出在右下部分空间即可。

代码:

class Solution {
public:
    int calDepth(TreeNode* root) {
        int h = 0;
        if (root->left) {
            h = max(h, calDepth(root->left) + 1);
        }
        if (root->right) {
            h = max(h, calDepth(root->right) + 1);
        }
        return h;
    }

    void dfs(vector<vector<string>>& res, TreeNode* root, int r, int c, const int& height) {
        res[r][c] = to_string(root->val);
        if (root->left) {
            dfs(res, root->left, r + 1, c - (1 << (height - r - 1)), height);
        }
        if (root->right) {
            dfs(res, root->right, r + 1, c + (1 << (height - r - 1)), height);
        }
    }

    vector<vector<string>> printTree(TreeNode* root) {
        int height = calDepth(root);
        int m = height + 1;
        int n = (1 << (height + 1)) - 1;
        vector<vector<string>> res(m, vector<string>(n, ""));
        dfs(res, root, 0, (n - 1) / 2, height);
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

执行用时：4 ms, 在所有 C++ 提交中击败了41.40%的用户
内存消耗：8.1 MB, 在所有 C++ 提交中击败了75.79%的用户
复杂度分析
时间复杂度： O(height × 2^height)，其中 height 是二叉树的高度。需要填充 (height + 1)×(2 ^height+1 − 1) 的数组。
空间复杂度： O(height)，其中 height 是二叉树的高度。空间复杂度主要是递归调用的栈空间，取决于二叉树的高度。注意返回值不计入空间复杂度。

方法二：广度优先搜索

思路与算法

我们也可以通过广度优先搜索来解决此题。首先通过广度优先搜索来得到二叉树的高度 height，然后创建一个行数为 m = height + 1，列数为 n = 2^height+1 − 1 的答案数组 res 放置节点的值（字符串形式）。使用广度优先搜索遍历每一个节点时，记录每一个节点对应的放置空间，每一个节点的值放置在对应空间的第一行正中间，然后其所在的行和列会将剩余空间划分为两部分（左下部分和右下部分），并把它的非空左子节点和非空右子节点以及它们的对应的放置空间放入队列即可。特别地，根节点的放置空间为整个 res 数组。

代码:

class Solution {
public:
    int calDepth(TreeNode* root) {
        int res = -1;
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            int len = q.size();
            res++;
            while (len) {
                len--;
                auto t = q.front();
                q.pop();
                if (t->left) {
                    q.push(t->left);
                }
                if (t->right) {
                    q.push(t->right);
                }
            }
        }
        return res;
    }

    vector<vector<string>> printTree(TreeNode* root) {
        int height = calDepth(root);
        int m = height + 1;
        int n = (1 << (height + 1)) - 1;
        vector<vector<string>> res(m, vector<string>(n, ""));
        queue<tuple<TreeNode*, int, int>> q;
        q.push({root, 0, (n - 1) / 2});
        while (!q.empty()) {
            auto t = q.front();
            q.pop();
            int r = get<1>(t), c = get<2>(t);
            res[r][c] = to_string(get<0>(t)->val);
            if (get<0>(t)->left) {
                q.push({get<0>(t)->left, r + 1, c - (1 << (height - r - 1))});
            }
            if (get<0>(t)->right) {
                q.push({get<0>(t)->right, r + 1, c + (1 << (height - r - 1))});
            }
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

执行用时：4 ms, 在所有 C++ 提交中击败了41.40%的用户
内存消耗：8.2 MB,在所有 C++ 提交中击败了40.00%的用户
复杂度分析
时间复杂度： O(height×2^height)，其中 height 是二叉树的高度。需要填充 (height + 1)×(2^height+1 − 1) 的数组。
空间复杂度：O(2^height)，其中 height 是二叉树的高度。空间复杂度主要是队列空间，队列中的元素个数不超过二叉树的节点个数，为 O(2^height )。注意返回值不计入空间复杂度。
author：LeetCode-Solution