牛客网刷题篇

作者：敲代码の流川枫

博客主页：流川枫的博客

专栏：和我一起学java

语录：Stay hungry stay foolish

工欲善其事必先利其器，给大家介绍一款超牛的斩获大厂offer利器——牛客网

点击免费注册和我一起刷题吧    

文章目录

表示数值的字符串

替换空格

斐波那契数列

 数字在升序数组中出现的次数

---

 

表示数值的字符串

请实现一个函数用来判断字符串str是否表示数值（包括科学计数法的数字，小数和整数）。

科学计数法的数字(按顺序）可以分成以下几个部分:

1.若干空格

2.一个整数或者小数

3.（可选）一个 'e' 或 'E' ，后面跟着一个整数(可正可负)

4.若干空格

小数（按顺序）可以分成以下几个部分：

1.若干空格

2.（可选）一个符号字符（'+' 或 '-'）

3. 可能是以下描述格式之一:

3.1 至少一位数字，后面跟着一个点 '.'

3.2 至少一位数字，后面跟着一个点 '.' ，后面再跟着至少一位数字

3.3 一个点 '.' ，后面跟着至少一位数字

4.若干空格

整数（按顺序）可以分成以下几个部分：

1.若干空格
2.（可选）一个符号字符（'+' 或 '-')

3. 至少一位数字

4.若干空格

例如，字符串["+100","5e2","-123","3.1416","-1E-16"]都表示数值。

但是["12e","1a3.14","1.2.3","+-5","12e+4.3"]都不是数值。

提示:

1.1 <= str.length <= 25

2.str 仅含英文字母（大写和小写），数字（0-9），加号 '+' ，减号 '-' ，空格 ' ' 或者点 '.' 。

3.如果怀疑用例是不是能表示为数值的，可以使用python的print(float(str))去查看

进阶：时间复杂度O(n)\O(n) ，空间复杂度O(n)\O(n) 

思路：

先trim，去掉字符串开头结尾的空格

.只能出现一次，且只能在e前面出现

e只能出现一次，且出现时前面应有数字

+ -只能出现在开头或e后面

空格，用trim处理，中间有空格时直接当失败返回

用boolean来表示每一个情况是否出现，只写成功的情况

题解：

    public boolean isNumeric (String str) {
     
        str = str.trim();
        //用boolean来表示每一个情况是否出现，是否出现一次（用!XXX来判断）
        boolean numFlag = false, dotFlag = false, eFlag = false, plusFlag = false;
        //只写成功的情况
        for(int i = 0; i < str.length(); i++){
            if(str.charAt(i) >= '0' && str.charAt(i) <= '9'){
                numFlag = true;
            }else if(str.charAt(i) == '.' && !dotFlag && !eFlag){
                dotFlag = true;
            }else if((str.charAt(i) == 'e' || str.charAt(i) == 'E') &&
                     !eFlag && numFlag){
                eFlag = true;
                //处理132e这种情况
                numFlag = false;
            }else if((str.charAt(i) == '+' || str.charAt(i) == '-') && 
                     (i == 0 || str.charAt(i-1) == 'e' || str.charAt(i-1) == 'E')){
                //什么也不干
            }else {
                return false;
            }
        }
        return numFlag;
    }

替换空格

请实现一个函数，将一个字符串s中的每个空格替换成“%20”。

例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。

数据范围:0 \le len(s) \le 1000 \0≤len(s)≤1000 。保证字符串中的字符为大写英文字母、小写英文字母和空格中的一种。

方法一

思路：先把字符串转换为单个字符

这里让求的是把字符串中的空格替换成%20，其中一种实现方式就是申请一个临时数组，然后再遍历这个字符串的每个字符，如果不是空格就把遍历的字符添加到临时数组中，如果是空格就添加3个字符'%'，'2'，'0'分别到临时数组中，最后再把临时数组转化为字符串即可。

    public String replaceSpace(String s) {
        int length = s.length();
        char[] array = new char[length * 3];
        int index = 0;
        for (int i = 0; i < length; i++) {
            char c = s.charAt(i);
            if (c == ' ') {
                array[index++] = '%';
                array[index++] = '2';
                array[index++] = '0';
            } else {
                array[index++] = c;
            }
        }
        String newStr = new String(array, 0, index);
        return newStr;
    }

时间复杂度：O（n），所有字符都遍历一遍
空间复杂度：O（n），需要一个n*3的数组 

方法二

思路：使用StringBuilder

把字符串中的每个字符一个个添加到StringBuilder中，如果遇到空格就把他换成%20

    public String replaceSpace(String s) {
        StringBuilder stringBuilder = new StringBuilder();
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == ' ')
                stringBuilder.append("%20");
            else
                stringBuilder.append(s.charAt(i));
        }
        return stringBuilder.toString();
    }

时间复杂度：O（n），所有字符都遍历一遍
空间复杂度：O（n），StringBuilder需要的空间

斐波那契数列

大家都知道斐波那契数列，现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项。

斐波那契数列是一个满足 fib(x)=\left\{ \begin{array}{rcl} 1 & {x=1,2}\\ fib(x-1)+fib(x-2) &{x>2}\\ \end{array} \right.fib(x)={1fib(x−1)+fib(x−2)​x=1,2x>2​ 的数列

数据范围：1\leq n\leq 401≤n≤40

要求：空间复杂度 O(1)O(1)，时间复杂度 O(n)O(n) ，本题也有时间复杂度 O(logn)O(logn) 的解法

输入描述：

一个正整数n

返回值描述：

输出一个正整数。

方法一

思路：迭代相加（推荐使用）

动态规划算法的基本思想是：将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解；对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果

斐波那契数列初始化第1项与第2项都是1，则根据公式第0项为0，可以按照斐波那契公式累加到第nnn项

具体做法：

1：低于2项的数列，直接返回n

2：初始化第0项，与第1项分别为0，1

3：从第2项开始，逐渐按照公式累加，并更新相加数始终为下一项的前两项

public class Solution {
    public int Fibonacci(int n) {
        //从0开始，第0项是0，第一项是1
        if(n <= 1)    
             return n;
         int res = 0;
         int a = 0;
         int b = 1;
         //因n=2时也为1，初始化的时候把a=0，b=1
         for (int i = 2; i <= n; i++){
         //第三项开始是前两项的和,然后保留最新的两项，更新数据相加
             res = (a + b);
             a = b;
             b = res;
         }
        return res;
    }
}

方法二

思路：递归

1、当 n < 2时，直接返回 n

2、递归算法：Fibonacci(n-1) + Fibonacci(n-2);

优点，代码简单好写，缺点：慢，会超时 时间复杂度：O(2^n) 空间复杂度：递归栈的空间

public class Solution {
    public int Fibonacci(int n) {
        if (n < 2){
            return n;
        }
        
        return Fibonacci(n-1) + Fibonacci(n-2);
    }
}

 数字在升序数组中出现的次数

给定一个长度为 n 的非降序数组和一个非负数整数 k ，要求统计 k 在数组中出现的次数

数据范围：0 \le n \le 1000 , 0 \le k \le 1000≤n≤1000,0≤k≤100，数组中每个元素的值满足 0 \le val \le 1000≤val≤100
要求：空间复杂度 O(1)O(1)，时间复杂度 O(logn)O(logn)

方法：二分法（推荐使用）

分治即“分而治之”，“分”指的是将一个大而复杂的问题划分成多个性质相同但是规模更小的子问题，子问题继续按照这样划分，直到问题可以被轻易解决；“治”指的是将子问题单独进行处理。经过分治后的子问题，需要将解进行合并才能得到原问题的解，因此整个分治过程经常用递归来实现。

思路：

因为data是一个非降序数组，它是有序的，这种时候我们可能会想到用二分查找。但是一个数组可能有多个k，而且我们要查找的并非常规二分法中k出现的位置，而是k出现的左界和k出现的右界。要是能刚好找到恰好小于k的数字位置和恰好大于k的数字的位置就好了

再有因为数组中全是整数，因此我们可以考虑，用二分查找找到k+0.5k+0.5k+0.5应该出现的位置和k−0.5k-0.5k−0.5应该出现的位置，二者相减就是k出现的次数

具体做法：

1：写一个二分查找的函数在数组中找到某个元素出现的位置。每次检查区间中点值，根据与中点的大小比较，确定下一次的区间

2：分别使用二分查找，找到k+0.5和k-0.5应该出现的位置，中间的部分就全是k，相减计算次数就可以了

 

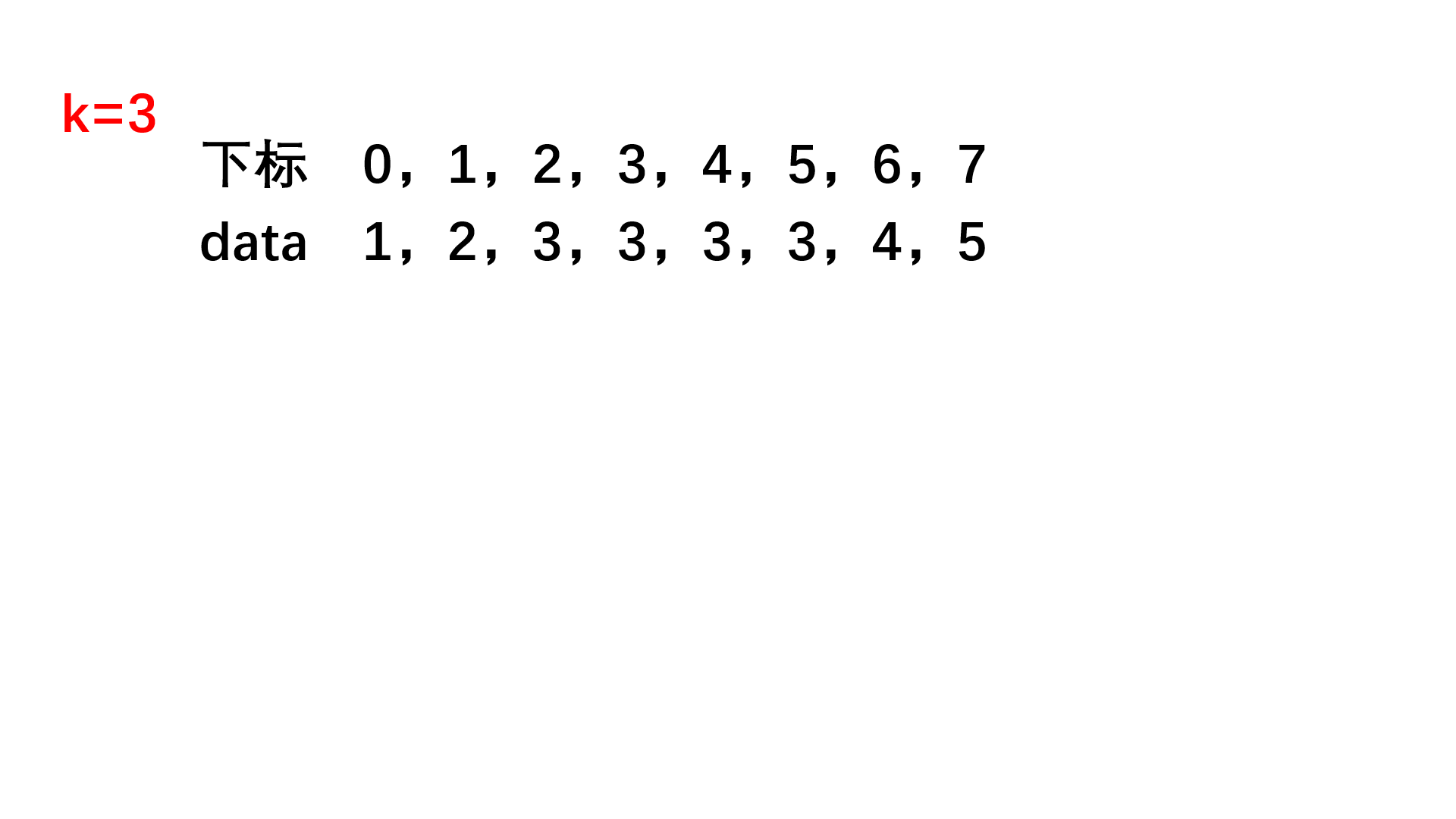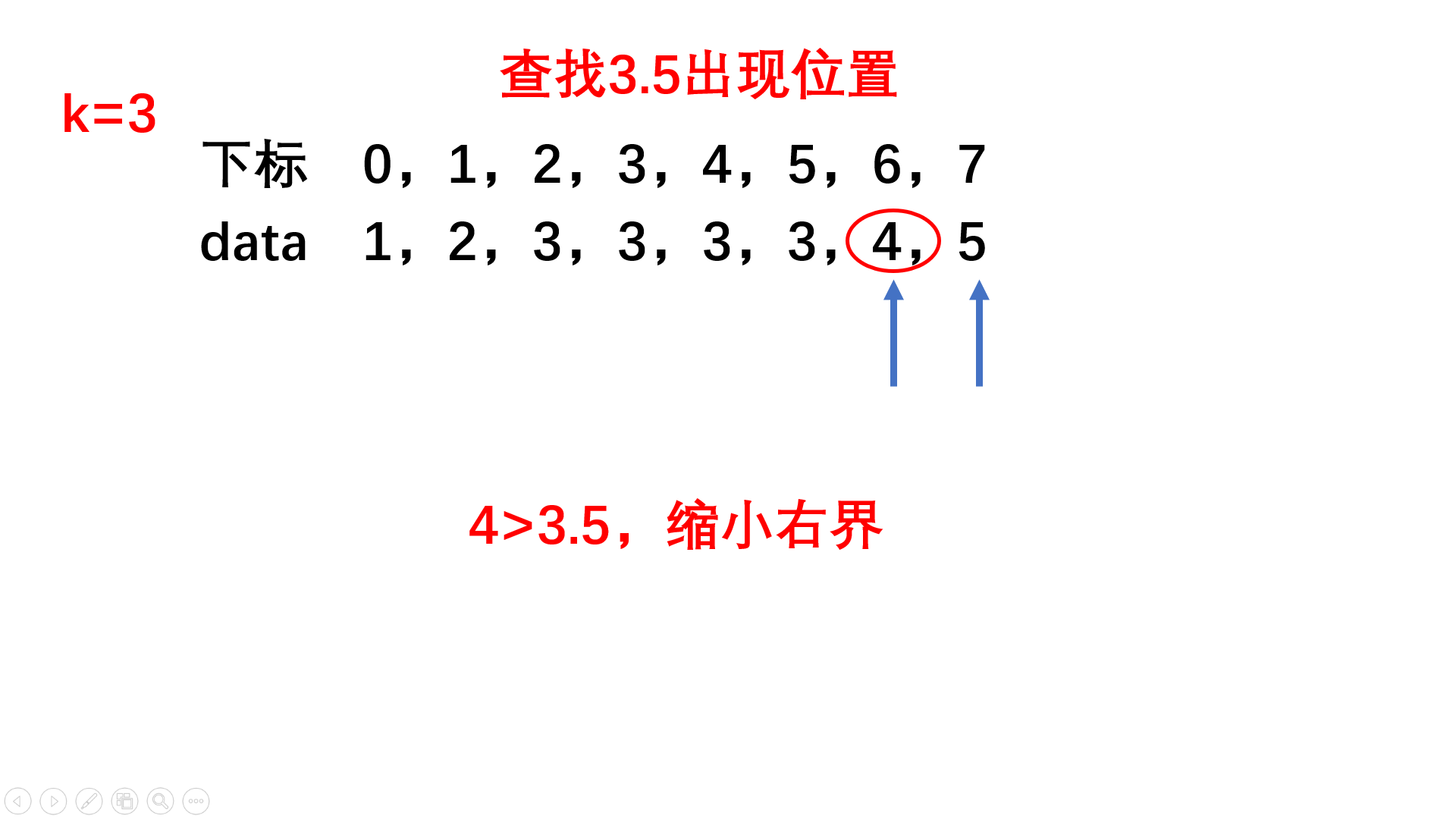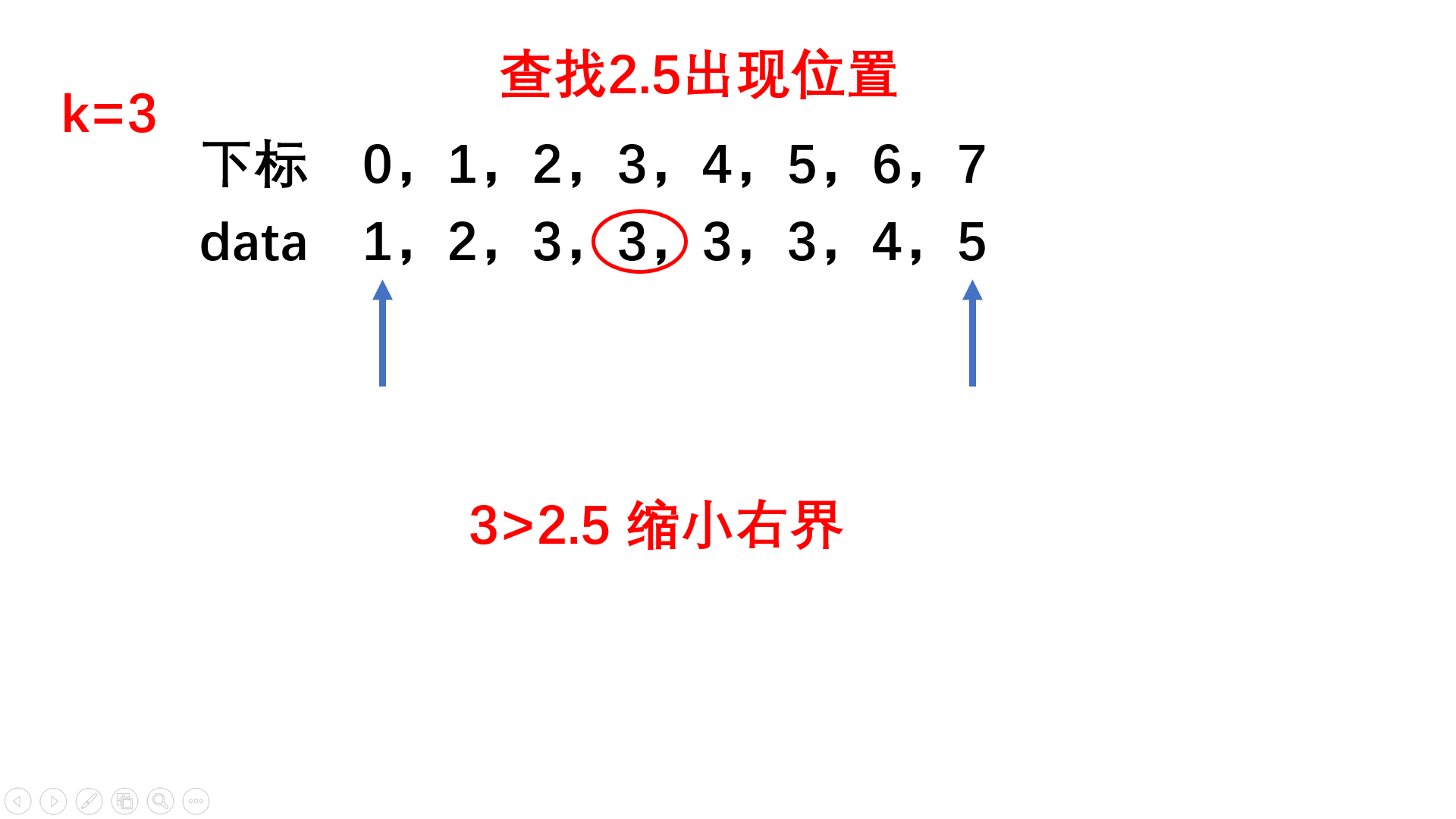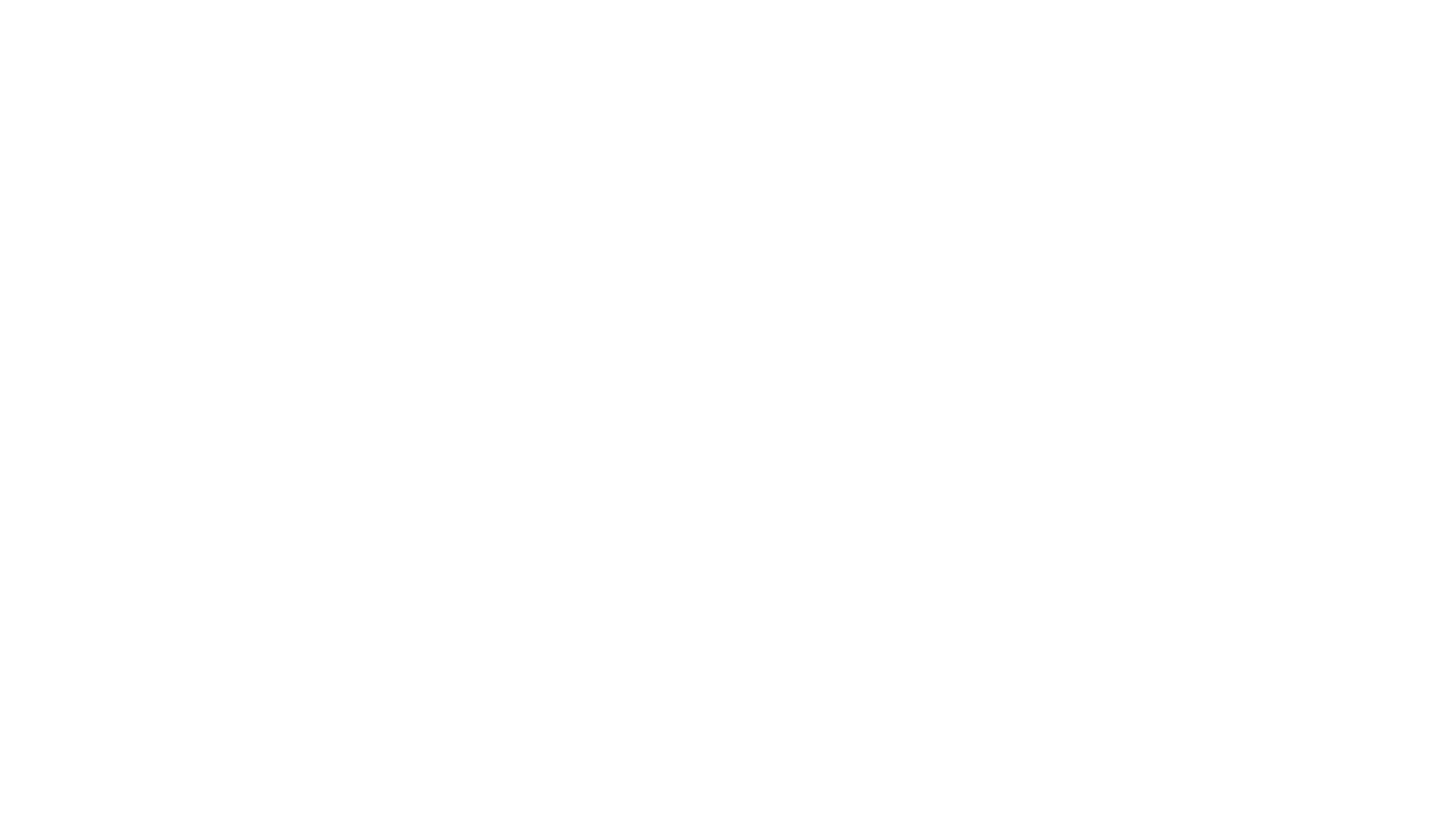
public class Solution {
    //二分查找
    private int bisearch(int[] data, double k){ 
        int left = 0;
        int right = data.length - 1;
        //二分左右界
        while(left <= right){ 
            int mid = (left + right) / 2;
            if(data[mid] < k)
                left = mid + 1;
            else if(data[mid] > k)
                right = mid - 1;
        }
        return left;
    }
    public int GetNumberOfK(int [] array , int k) {
        //分别查找k+0.5和k-0.5应该出现的位置，中间的部分就全是k
        return bisearch(array, k + 0.5) - bisearch(array, k - 0.5);
    }
}

时间复杂度：O(log2n)O(log_2n)O(log2​n)，其中nnn为数组长度，两次二分查找，二分查找复杂度为O(log2n)O(log_2n)O(log2​n)

空间复杂度：O(1)O(1)O(1)，常数级变量，无额外辅助空间

“ 本期的分享就到这里了， 记得给博主一个三连哈，你的支持是我创作的最大动力！