来自北大算法课的Leetcode题解：189. 轮转数组

代码仓库：Github | Leetcode solutions @doubleZ0108 from Peking University.

• 解法1(超时)：按照题意，一次一次做循环，用一个变量保存

  • 改进1(超时): 轮转次数k对数组长度取余，如果正好转一圈回来就不用转了
  • 改进2(T68% S32%)：用空间换时间，开辟$O(k)$的空间直接把结尾k个元素存下来，前面元素直接移动完再放到开头，由于改进1，所以空间复杂度也还好

• 解法2(T47% S14%): 能不能不开辟空间保存这些被移出来的元素，或者说能不能让他们也参与到+k的轮换中呢？

  基础想法很简单，如果一个元素往右移出了数组长度，就对他的位置取余，这个思想是很简单的。

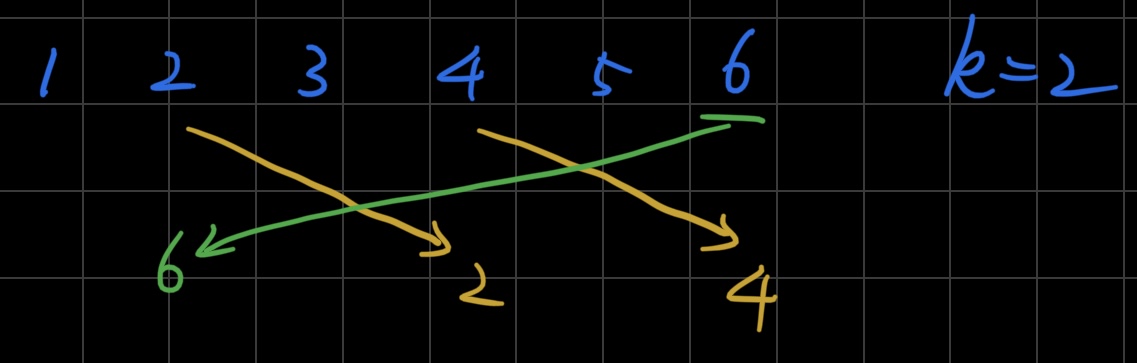
  但复杂在移动完一个元素后必须直接再移动将要填到原位置的元素，这样才能避免数组元素被覆盖，比如我可以先把最后一个元素6保存下来，然后先去用4填补6的空位，再用2去填补4的空位，这样看起来也没有很复杂。

  但更恶心的是如果移动的是偶数次，或者移动数是数组长的语数6，就会发生这样的问题，本来要保存最后放的6被提前覆盖了，之后就会不断在这几个数中循环导致错误，因此此时正常的填完6之后，要往前一位到5，把保留的数替换为5，保留的最后位置就是当前5的位置+k%n

• 解法3(T95% S66%): 数组反转，首先数组整体反转一遍，然后前k个数反转一遍，最后k之后的数再反转一遍

  • 注意python的reversed()会生成新的数组，就不算修改引用，因此leetcode中结果还是原数组

  1 2 3 4 5 6 (k=2) 原始
  6 5 4 3 2 1       整体反转
  5 6 | 1 2 3 4     左右分别反转
  1
  2
  3

class Solution(object):
    def rotate(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: None Do not return anything, modify nums in-place instead.
        """
        n = len(nums)     
        k %= n
        if k==0: return

        def reverse(i, j):
            while i < j:
                nums[i], nums[j] = nums[j], nums[i]
                i += 1
                j -= 1

        reverse(0, n-1)
        reverse(0, k-1)
        reverse(k, n-1)

    def otherSolution(self, nums, k):
        # 解法2
        n = len(nums)
        k %= n

        if k==0: return

        idx = n-1
        tmp = nums[idx]
        pos = k-1
        for _ in range(n-1):
            if idx == pos:
                nums[idx] = tmp
                idx = (idx - 1 + n) % n
                pos = (idx + k) % n
                tmp = nums[idx]
            else:
                nums[idx] = nums[idx-k]
                idx = (idx - k + n) % n
        nums[pos] = tmp

        # 解法1 改进2
        k %= len(nums)
        tmps = nums[len(nums)-k:]
        nums[k:] = nums[:len(nums)-k]
        nums[:k] = tmps
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47