用队列式广度优先算法解决背包问题

一 问题描述

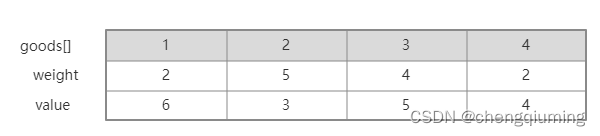
有一个背包和 4 个物品，每个物品的重量和价值都如下图所示，背包的容量 W=10,求在不超过背包容量的前提下，把哪些物品放入背包才能获得最大价值。

二 实现

package com.platform.modules.alg.alglib.p932;
 
import java.util.LinkedList;
import java.util.Queue;
 
public class P932 {
    public String output = "";
    public static final int N = 10;
    boolean bestx[] = new boolean[N];
    Goods goods[] = new Goods[N];
    Integer bestp;
    int W;
    int n;
    int sumw;
    int sumv;
 
    public String cal(String input) {
        String[] line = input.split("\n");
        String[] words = line[0].split(" ");
        // 物品的个数和背包的容量
        n = Integer.parseInt(words[0]);
        W = Integer.parseInt(words[1]);
        bestp = 0; // bestv 用来记录最优解
        sumw = 0; // sumw 为所有物品的总重量。
        sumv = 0; // sumv为所有物品的总价值
        words = line[1].split(" ");
        for (int i = 1; i <= words.length / 2; i++) { // 输入每个物品的重量和价值,用空格分开
            goods[i].weight = Integer.parseInt(words[2 * i - 2]);
            goods[i].value = Integer.parseInt(words[2 * i - 1]);
            sumw += goods[i].weight;
            sumv += goods[i].value;
        }
        if (sumw <= W) {
            bestp = sumv;
            output = bestp.toString();
            return output;
        }
        bfs();
        output += bestp.toString() + "\n";
        for (int i = 1; i <= n; i++) { // 输出最优解
            if (bestx[i])
                output += i + "  ";
        }
        return output;
    }
 
    public P932() {
        for (int i = 0; i < goods.length; i++) {
            goods[i] = new Goods();
        }
    }
 
    int bfs() { // 队列式分支限界法
        int t, tcp, trp, trw; // 当前处理的物品序号t，装入背包物品价值 tcp,剩余容量 trw
        Queue q = new LinkedList<>(); // 创建一个普通队列(先进先出)
        q.add(new Node(0, sumv, W, 1)); // 压入一个初始节点
        while (!q.isEmpty()) {
            // 定义三个结点型变量
            Node livenode = new Node();
            Node lchild = new Node();
            Node rchild = new Node();
            livenode = q.peek(); // 取出队头元素作为当前扩展结点 livenode
            q.poll(); // 队头元素出队
            t = livenode.id; // 当前处理的物品序号
            // 搜到最后一个物品的时候不需要往下搜索
            // 如果当前的背包没有剩余容量(已经装满)了，不再扩展
            if (t > n || livenode.rw == 0) {
                if (livenode.cp >= bestp) { // 更新最优解和最优值
                    for (int i = 1; i <= n; i++)
                        bestx[i] = livenode.x[i];
                    bestp = livenode.cp;
                }
                continue;
            }
            if (livenode.cp + livenode.rp < bestp) // 判断当前结点是否满足限界条件，如果不满足不再扩展
                continue;
            tcp = livenode.cp; // 当前背包中的价值
            trp = livenode.rp - goods[t].value; // 不管当前物品装入与否，剩余价值都会减少。
            trw = livenode.rw; //背包剩余容量
            if (trw >= goods[t].weight) { //扩展左孩子，满足约束条件，可以放入背包
                lchild.rw = trw - goods[t].weight;
                lchild.cp = tcp + goods[t].value;
                lchild = new Node(lchild.cp, trp, lchild.rw, t + 1);
                for (int i = 1; i < t; i++) // 复制以前的解向量
                    lchild.x[i] = livenode.x[i];
                lchild.x[t] = true;
                if (lchild.cp > bestp) // 比最优值大才更新
                    bestp = lchild.cp;
                q.add(lchild); // 左孩子入队
            }
            if (tcp + trp >= bestp) {//扩展右孩子,满足限界条件，不放入背包
                rchild = new Node(tcp, trp, trw, t + 1);
                for (int i = 1; i < t; i++)//复制以前的解向量
                    rchild.x[i] = livenode.x[i];
                rchild.x[t] = false;
                q.add(rchild); // 右孩子入队
            }
        }
        return bestp;// 返回最优值
    }
}
 
// 定义结点。每个节点来记录当前的解。
class Node {
    int cp; // cp 为当前装入背包的物品总价值
    int rp; // rp为剩余物品的总价值
    int rw; // 剩余容量
    int id; // 物品号
    boolean x[] = new boolean[P932.N]; //解向量
 
    Node() {
    }
 
    Node(int _cp, int _rp, int _rw, int _id) {
        cp = _cp;
        rp = _rp;
        rw = _rw;
        id = _id;
    }
}
 
// 物品
class Goods {
    int weight; //重量
    int value; //价值
}

三 测试