【考研线代】一. 行列式

第一章 行列式

1.1 行列式的概念

行列式是一个数，是不同行不同列元素乘积的代数和

n阶排列：由1，2，3…，n组成的有序数组称为一个n阶排列。

逆序：如果一个大的数排在小数前面，则称这两个数构成了逆序。

逆序数：逆序的总数。

偶排列，奇排列：根据逆序数的奇偶性判断。

n阶行列式：偶排列前面带正号，奇排列前面带负号。

完全展开式：

适用于二阶和三阶行列式的展开方法：沿着正对角线相乘 - 沿着反对角线相乘 的 数

1.2 行列式的性质

1. 转置的行列式（行列互换），值不变。

$$|A^T|=|A|$$

所以后续的性质中，如果行可以，那么列也可以。

2. 把行列式中某一行（列）的所有元素都乘以一个数K，等于用数K乘以行列式。

特别的，如果某行的元素全都是0，那么行列式的值为0。

3. 对换行列式中两行（列）的位置，行列式反号。

存在下面的特例：

• 两行相同，行列式为0
• 两行成比例，结合性质2，行列式依旧为0

4. 如果行列式的某行(列）的各元素是两个元素之和，那么这个行列式等于两个行列式的和。

5. 把一行（列）的倍数 k 加到另一行（列），行列式不变。(使用频率最高)

1.3 行列式的展开与计算

余子式：去掉第i行j列得到的n-1阶的行列式。

代数余子式：带有-1的i+j次方的余子式
$$A_{ij}=(-1{)}^{i+j}{M}_{ij}$$
展开定理：通过展开某一行，乘对应位置的代数余子式
$$|A|=a_{i1}{A}_{i1}+a_{i2}{A}_{i2}+...+a_{im}{A}_{im}$$

• 相反：某一行的所有元素和 另一行相应元素的代数余子式 乘积之和等于0。

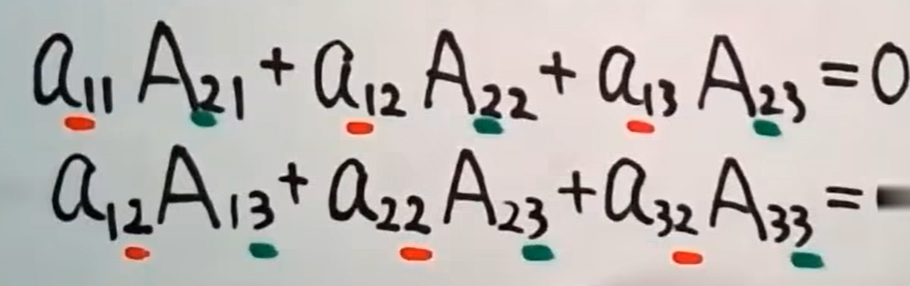
• 上三角或者下三角的行列式的值 = 对角线的值累乘
• 反三角的行列式的值，还需要判断一下逆序数的奇偶性。

• 两个拉普拉斯的展开式

• 范德蒙行列式：看到了直接写答案——连乘积

形式：第一行全是1，纵向看是幂的关系，计算时横向两两相减后相乘。

结论：

心得：

• 遇到爪型的行列式，尝试通过累加消去首行或者首列的内容。
• 遇到常规行列式，计算的时候需要先构造出几个0来，方便计算。
• 遇到有规律的0分布，可以考虑通过换行或者换列，再应用拉普拉斯展开式。
• 遇到对角线带未知数x 的行列式，求行列式分析其为三次方程时，分析哪两个数加加减减为0，就去消！注意提取x的公因数。

1.4 克拉默法则

• n个方程，n个未知数，且系数行列式|A| ！=0，那么方程组有唯一解
• 该方程的解为：

$$x_i=|\frac{A_i}{A}|$$

|A|是系数行列式，|Ai| 是第i列元素替换为方程右端常数项构成的行列式。

• 推论：

$$齐次线性方程组的系数行列式|A|\ne 0⟷方程组有唯一零解$$

推论-反：
$$齐次线性方程组的系数行列式|A|=0⟷方程组存在非零解$$
用处：

1. 可以考虑用克拉默法则来解方程
2. 可以使用推论来证明行列式 = 0

例：若某某带未知数λ的齐次方程组仅有零解，求λ
思路：令系数行列式不等于0，求解即可。

不算刷题的话，感觉这第一章内容不是很多的说。