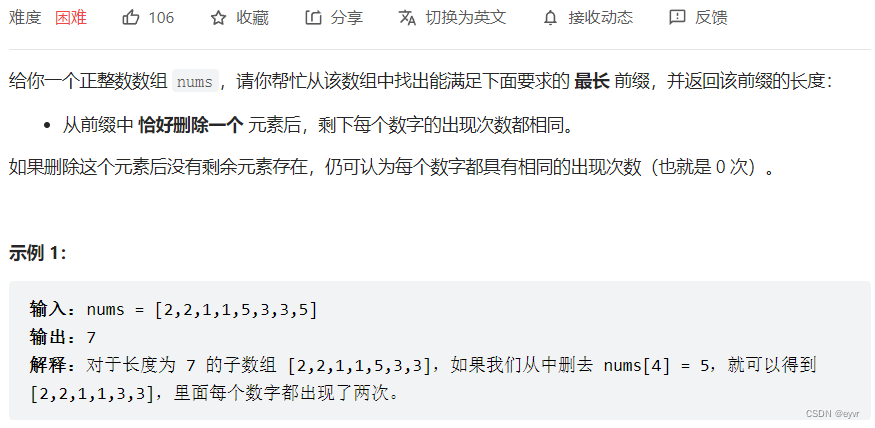
1224. 最大相等频率（数组）

先从逻辑上解决问题，再通过代码实现，最后再优化
满足条件的前缀有三种：

1. 所有数字都只出现一次
2. 只有一个数字出现一次，其他数字出现的次数相同
3. 其他数字出现的次数相同，只有一个数字出现的次数比其他数字多一
   首先需要一个哈希表（题目数据限定了1-100000，也可以用数组且更快）来存储每个数字出现的次数
   如何统计出现x次的数字有多少个？
   显然在条件下x的种类是有限的，最多为两种（1、1。2、1和一个数。3、两个相邻的数）
   定义m为数字最大出现的次数，n为出现m次的数字的个数，a为所有出现的不同的数字的个数
   条件转化为：
4. m = 1，n = a
5. n = a - 1，排除的数字只出现一次
6. n = 1，其他数字的出现次数都小一
   代码实现

class Solution {
    public int maxEqualFreq(int[] nums) {
        Map<Integer,Integer> m = new HashMap<>();
        Map<Integer,Integer> f = new HashMap<>();
        int maxf = 0, ans = 0;
        for(int i = 0; i < nums.length; i++){
            m.put(nums[i], m.getOrDefault(nums[i],0) + 1);
            f.put(m.get(nums[i]), f.getOrDefault(m.get(nums[i]), 0) + 1);
            f.put(m.get(nums[i]) - 1, f.getOrDefault(m.get(nums[i]) - 1, 0) - 1);
            if(f.get(m.get(nums[i]) - 1) == 0)
                f.remove(m.get(nums[i]) - 1);
            maxf = Math.max(maxf, m.get(nums[i]));
            if(f.size() == 3 && f.get(maxf) == 1 && f.containsKey(maxf - 1))
                ans = i;
            if(f.size() == 3 && f.containsKey(1) && f.get(1) == 1)
                ans = i;
            if(maxf == 1)
                ans = i;
        }
        if(m.size() == 1)
            return nums.length;
        return ans + 1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

代码很直观，每增加一个数字就对两个哈希表进行修改，并判断是否满足条件
最后判断一个特例，整个数组只有一种数字
虽然能通过测试，但是由于频繁的修改，查询哈希表时间上并不是很理想

下面给出优化后的解
首先不用哈希表，用数组存储每个数字出现的次数
对于第二种情况，由于要知道出现次数为1的数字的个数，所以使用哈希表存储了每一个出现次数所包含的数字的个数
但是事实上并不需要，只需要保存最大出现的次数，和对应该次数的数字的个数就可以推出是否有一个数字出现次数为1，因为总共统计的数字个数为i+1，所以当所有出现次数为最大值的数字的个数之和等于 i 时就只剩下了一个数字，该数字出现次数为 1
同样的对于第三种情况，最多出现的数字的出现次数为maxFreq，那么剩下 i + 1 - maxFreq 个数字且不同的有 n - 1种（n为出现的不同的数字的个数），所以最后等到一个关系式 （i + 1 - maxFreq）/ （n - 1）= maxFreq - 1 化简后的到 maxFreq == i / n + 1

class Solution {
    public int maxEqualFreq(int[] nums) {
        int[] cnt = new int[(int) (1e5) + 1];
        int maxFreq = 0, maxN = 0, N = 0, ans = 0, n = nums.length;
        for (int i = 0; i < n; i++) {
            int num = nums[i];
            if (cnt[num]++ == 0) {
                N++;
            }
            if (cnt[num] > maxFreq) {
                maxFreq = cnt[num];
                maxN = 1;
            } else if (cnt[num] == maxFreq) {
                maxN++;
            }
            if (maxFreq == 1 || maxFreq * maxN == i || maxN == 1 && maxFreq == i / N + 1) {
                ans = i + 1;
            }
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22