ICML 2020 | GCNII：简单和深度图卷积网络

前言

题目： Simple and Deep Graph Convolutional Networks
会议： ICML 2020
论文地址：Simple and Deep Graph Convolutional Networks

GCN是一种强大的图结构数据深度学习方法，GCN及其后续变体在现实世界数据集的各个应用领域中表现出了卓越的性能。尽管GCN取得了成功，但由于过度平滑问题，目前大多数GCN模型都是浅层的。

所谓过度平滑问题，是指随着GCN的深度增加，越来越多的节点表示倾向于收敛到某个固定的值，从而变得不可区分，这会大大降低模型的性能。

为了缓解过平滑问题，本文提出了GCNII，它是普通GCN模型的扩展，GCNII通过使用两种简单而有效的技术来缓解过平滑问题：初始残差和恒等映射。

1. 基础知识

符号定义：


上述符号定义和之前的文章类似，不再解释。

下面详细介绍了三种GCN模型，随后引出了本文的提出的GCNII模型。

1.1 Vanilla GCN

即Kipf于2017年提出的GCN，GCN认为，图的卷积运算可以用拉普拉斯算子的$K$阶多项式来近似：

这里$\theta \in R^{K+1}$，在Kipf提出的GCN中，采用系数${\theta }_0=2\theta$和${\theta }_1=-\theta$的对$k$阶多项式进行逼近($k=1$)，由此我们得到基本的GCN卷积运算操作：

GCN中用$\tilde{P}={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$来代替上式中的$I+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$，其中$\tilde{A}=A+I$，$\tilde{D}=D+I$。

最终得到的卷积表达式为：

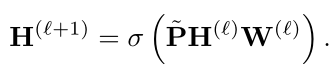
这里$\sigma$代表ReLU激活函数。

GCN的引申SGC请参考：ICML 2019 | SGC：简单图卷积网络。

1.2 APPNP

APPNP利用个性化PageRank导出$K$阶固定滤波器。设$f_{\theta }(X)$表示特征矩阵$X$经过两个全连接层后的输出，那么PPNP模型可以表示如下：

由于个性化PageRank的特性，该滤波器保持局部性，因此适合于分类任务。PPNP的作者后续提出了APPNP，一个能进行K-hop聚合的APPNP被定义为：

这里$H^{(0)}=f_{\theta }(X)$。通过特征变换和传播，PPNP和APPNP可以在不增加神经网络层数的情况下聚合来自多跳邻居的信息。

1.3 JKNet

JKNet是第一个深度GCN框架。JKNet在最后一层将之前所有层的节点表示$[H^{(1)},...,H^{(K)}]$结合到一起，用以学习不同子图结构的不同阶表示，通过结合来自以前层的所有表示，JKNet缓解了过度平滑的问题。

1.4 DropEdge

DropEdge表明，从图中随机移除一些边会延缓过平滑的收敛速度。用$P_{drop}$表示随机删除一些边后的图卷积矩阵，带有DropEdge的Vanilla GCN被定义为：

2. GCNII

这一节介绍本文提出的GCNII模型。

Vanilla GCN中固定的系数$\theta$限制了多层GCN的表达能力，从而导致了过平滑。为了将GCN扩展到真正深入的模型，我们需要使GCN能够表示任意系数的$K$阶多项式滤波器。形式上，将GCNII的第$\ell$层定义为：

这里${\alpha }_{\ell }$和${\beta }_{\ell }$是两个超参数，$\tilde{P}={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$是图卷积矩阵。

GCNII与Vanilla GCN相比，做了两点改进：

1. 将平滑的节点表示$\tilde{P}{H}^{(\ell )}$与初始的$H^{(0)}$通过一个初始残差连接(initial residual connection)起来，也就是式子的第一部分。
2. 给权重矩阵$W^{(\ell )}$添加了一个identity mapping，也就是恒等映射，即公式中的$I_n$。

2.1 初始残差连接

为了模拟ResNet中的skip connection，(Kipf & Welling, 2017)提出将平滑的节点表示$\tilde{P}{H}^{(\ell )}$和$H^{(\ell )}$进行连接。然而，(Kipf & Welling, 2017)也表明，这种残差连接只能部分缓解过平滑问题，当我们堆叠更多的层时，模型的性能仍然会下降。

因此，本文作者提出，不使用残差连接来携带来自前一层的信息，而是构造一个与初始表示$H^{(0)}$的连接。有了初始残差连接之后，即使我们堆叠许多层，也能确保每个节点的最终表示至少保留来自输入特征的一小部分(${\alpha }_{\ell }$)。在真正实践中，我们可以简单地设置${\alpha }_{\ell }$的值为0.1或0.2，以便每个节点的最终表示至少包含输入特征的一部分。

此外，作者认为，$H^{(0)}$不一定是特征矩阵$X$。如果$X$中特征维数$d$较大，我们可以在$X$上应用全连接神经网络，在正向传播之前得到一个低维的初始表示$H^{(0)}$。

回忆一下前面提到的APPNP：

APPNP中采取了类似的初始残差连接方法，不过，APPNP的作者表明，对特征矩阵进行多次非线性操作会导致过拟合，从而导致性能下降。因此，APPNP采用的是不同层之间的线性组合，因此仍然是浅层模型。这表明，仅凭初始残差的思想不足以将GCN扩展到深度模型。

2.2 恒等映射

首先放上GCNII第$\ell$层的定义：

前面表明，仅凭初始残差的思想不足以将GCN扩展到深度模型。为了弥补APPNP中的不足，GCNII借鉴了ResNet中恒等映射(identity mapping)的思想：在权重矩阵$W^{(\ell )}$中加入了一个单位矩阵$I_n$。

文章总结了在模型中引入恒等映射的动机：

1. 与ResNet的动机类似，恒等映射确保深度GCNII模型至少能够达到与浅层版本相同的性能。 可以发现，如果${\beta }_{\ell }$足够小，深度GCNII将忽略权值矩阵$W^{(\ell )}$，本质上模拟了APPNP。
2. 据观察，特征矩阵不同维度之间的频繁交互会降低半监督任务中模型的性能。将平滑表示$\tilde{P}{H}^{(\ell )}$直接映射到输出减少了这种交互作用。
3. 恒等映射被证明在半监督任务中特别有用。一些文章表明，线性ResNet形式的$H^{(\ell +1)}=H^{\ell }(W^{\ell }+I_n)$满足以下性质：1)最优权矩阵$W^{(\ell )}$具有小范数；2)唯一的临界点是全局最小值。第一个性质允许我们对$W^{(\ell )}$进行强正则化以避免过拟合，而后一个性质在训练数据有限的半监督任务中是可取的。
4. 一些文章从理论上证明了$K$层GCN的节点特征会收敛到子空间并产生信息丢失。特别地，收敛速度依赖于$s^K$，其中$s$是权重矩阵$W^{(\ell )}$的最大奇异值，其中$\ell =0,1,...,K-1$。通过将$W^{(\ell )}$替换为$(1-{\beta }_{\ell })I_n+{\beta }_{\ell }{W}^{(\ell )}$以及对$W^{(\ell )}$是施加正则化，可以减小$W^{(\ell )}$的范数。此时，$(1-{\beta }_{\ell })I_n+{\beta }_{\ell }{W}^{(\ell )}$的奇异值将接近1。因此，最大奇异值$s$也会趋近于1，这意味着$s^K$较大，减轻了信息损失。

${\beta }_{\ell }$的设置原则：保证随着模型深度增加，权重矩阵$W^{(\ell )}$的衰减应该自适应地进行增大。因此，本文设计的${\beta }_{\ell }$的表达式如下：

其中$\lambda$是一个超参数。可以发现，随着层数$\ell$的增加，${\beta }_{\ell }$将会减小，这也就意味着公式中的${\beta }_{\ell }{W}^{(\ell )}$会相应减小。

3. 实验

数据集：

除了前面第一节提到的各种模型，本文的对比模型还包括GCNII的一种变体GCNII${}^{\ast }$，GCNII${}^{\ast }$的表达式如下：

而GCNII的表达式如下：

通过与GCNII对比可知，GCNII${}^{\ast }$为平滑表示$\tilde{P}{H}^{(\ell )}$施加了不同的权重矩阵和初始残差。

3.1 半监督节点分类

实验结果：

实验结果表明，GCNII和GCNII${}^{\ast }$在三个数据集上均实现了最佳性能。最近的两个深度模型JKNet和IncepGCN(DropEdge)并没有比浅层模型APPNP表现更好。值得注意的是，GCNII和GCNII${}^{\ast }$的深度达到了64层，这表明了深度网络结构具有优越性。

表3总结了不同层数的深度模型的结果：

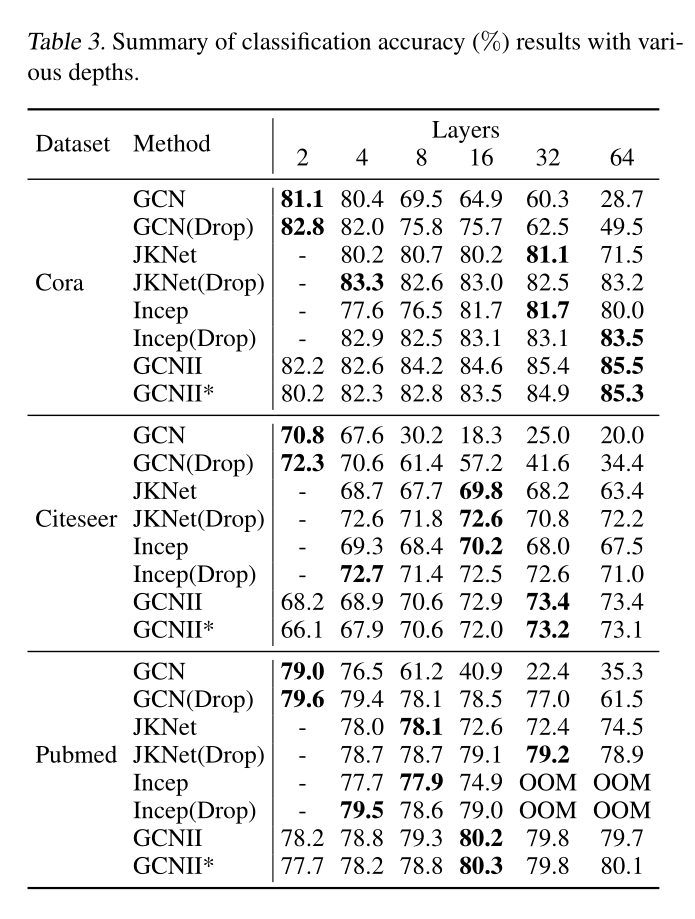
可以观察到，在Cora和Citeseer数据集上，随着层数增加，GCNII和GCNII${}^{\ast }$的性能不断提高。在Pubmed数据集上，GCNII和GCNII${}^{\ast }$在16层上获得了最好的结果，并且将网络深度增加到64层时二者都保持了类似的性能，作者将这种特性归功于identity mapping技术。

总之，结果表明，通过initial residual和identity mapping，我们可以解决过平滑问题，并将普通的GCN扩展到一个真正深入的模型。作为对比，当层数超过32时，使用DropEdge和JKNet的GCN性能会迅速下降，这意味着它们仍然无法解决过度平滑的问题。

3.2 监督节点分类

在监督节点分类任务中，对于每个数据集，将每个类的节点随机分为60%、20%和20%，用于训练、验证和测试，然后在10次随机分割中衡量所有模型在测试集上的性能。在所有数据集上，我们将学习率固定为0.01，dropout固定为0.5，隐藏单元数量固定为64，并执行超参数搜索来基于验证集调整其他超参数。

实验结果：

观察实验结果可知，GCNII和GCNII${}^{\ast }$在7个数据集中的6个上实现了最佳的性能，这证明了深度GCNII框架的优越性。值得注意的是，GCNII${}^{\ast }$在Wisc数据集上的精度比APPNP高出12%以上。这一结果表明，通过将非线性引入每一层，GCNII的预测能力强于线性模型APPNP。

3.3 归纳学习

实验结果：

实验结果显示，GCNII和GCNII${}^{\ast }$在PPI上实现了最佳的性能，并且GCNII是通过9层模型实现了这种性能，而所有基线模型的层数都小于或等于5，这表明归纳学习中也可以通过增加网络深度来提升模型的预测能力。

3.4 GCN的过平滑分析

一些文章证明，节点的度数越高，越容易过度平滑。为了验证这一猜想，本文作者研究了Cora、Citeseer和Pubmed上半监督节点分类任务的分类精度随节点度变化的情况。更具体地说，根据度对每个图的节点进行分组。第$i$组由度在$[2i,2i+1)$范围内的节点组成。对于每一组，报告了残差连接的GCN在不同网络深度下的平均分类精度如图1所示：

观察上图可知，双层GCN模型的精度随着节点度的增加而增加，这是意料之中的，因为度高的节点通常能从相邻节点获得更多的信息。但是，随着网络深度的扩大，高阶节点的精度下降速度比低阶节点快。值得注意的是，64层的GCN无法对度大于100的节点进行分类，这说明过平滑确实对度高的节点影响更大。

3.5 消融实验

消融实验主要是为了评估初始残差连接和恒等映射两种技术的作用，图2显示了消融研究的结果：

可以观察到：

1. 直接将恒等映射应用到普通GCN，略微延迟了过平滑的效果。
2. 直接将初始残差连接应用于Vanilla GCN，可以明显缓解过平滑。不过，2层模型仍然取得了最好的性能。
3. 同时使用初始残差连接和恒等映射，可以保证精度随网络深度的增加而增加。

4. 总结

本文提出了一种新的GCN模型GCNII，与Vanilla GCN相比，GCNII中引入了初始残差和恒等映射两种简单而有效的技术，这两种技术可以有效缓解深度GCN模型的过平滑问题。

理论分析表明，GCNII可以表示任意系数的$K$阶多项式滤波器。对于多层的普通GCN，本文证明图中节点度越高越容易出现过度平滑。实验结果表明，深度GCNII模型在半监督任务和监督任务上都取得了最优的性能。

关于未来方向，作为认为一是可以将GCNII与注意机制相结合，二是使用ReLU激活函数来分析GCNII的行为。