一. K均值聚类：物以类聚、人以群分

聚类算法是数据挖掘中的一项重要技术，其目的是使聚类后同一类的数据尽可能聚集在一起，不同的数据尽可能分离。聚类模型既有有监督的场景又有无监督的场景。经过一定的改造，还可以适用于半监督的场景。

常见的非监督式的聚类模型有：

1. 原型聚类：原型聚类是指聚类结构能通过一组原型刻画。原型是指样本空间中具有代表性的点。通常情况下，算法先对原型进行初始化，然后对原型进行迭代更新求解。常见的算法有k-均值聚类、学习向量量化、高斯混合聚类
2. 密度聚类：从样本的分布密度出发考虑样本间的可连接性，并基于可连接性样本不断扩展聚类簇以获得最终的聚类结果。常见的算法有DBSCAN
3. 层次聚类：在不同层次对数据集进行划分，从而形成树型的聚类结构。常见的算法有AGNES

1.1 距离的概念

在聚类模型中，刻画样本间的“距离”是非常重要、也是最本质的内容。距离𝐷𝑖𝑠𝑡(∗,∗)是作用在两个元素上的函数，需要满足一定的性质：
非负性：𝐷𝑖𝑠𝑡(𝑋,𝑌)≥0
同一性：𝐷𝑖𝑠𝑡(𝑋,𝑌)=0< = >𝑋=𝑌
对称性：𝐷𝑖𝑠𝑡(𝑋,𝑌)=𝐷𝑖𝑠𝑡(𝑌,𝑋)
直递性：𝐷𝑖𝑠𝑡(𝑋,𝑌)≤𝐷𝑖𝑠𝑡(𝑋,𝑍)+𝐷𝑖𝑠𝑡(𝑍,𝑌)

1.2 闵可夫斯基距离

对于数值型变量$X=(x_1,x_2,\dots ,x_n)$与$Y=(y_1,y_2,\dots ,y_n)$，可用闵可夫斯基距离来定义二者的距离：

容易验证闵氏距离符合性质1~3.
当p=1时，闵氏距离也称为曼哈顿距离
当p=2时，闵氏距离也称为欧式距离

注：
需要考虑到不同尺度的变量对距离的影响， 因此有时需要做归一化
需要考虑变量重要性的异同。可以加权重。

1.3 VDM距离

当变量是类别型时，如何定义距离？常用的方法有：值差度量(Value Difference Metric, VDM)、最小风险化度量(Minimum Risk Metric, MRM)、基于熵的度量(Entropy-Based Metric, EBM)、基于频率的度量(Frequency-Based Metric, FBM)等等。其中，VDM是最简单、常用的方法（但是依赖于变量独立假设）。
令$m_{(}u,a)$表示在变量u上取值为a的样本数，$m_{(}u,a,i)$表示在第i个样本簇中在变量u上取值为a的样本数。假设共有k个簇，则变量u上两个离散值a和b的VDM距离为

1.4 聚类模型中的基本概念

簇：聚类任务将样本划分为若干互不相交的子集。则每个子集称为一个“簇”
均值向量：簇中样本点的几何中心，即对于某个簇C，其均值向量为

1.5 K-均值聚类（K-means）

1.6 K-均值算法的求解步骤

K均值采用贪心策略，迭代地寻找出最优（或次优解）

1.7 K-均值算法的参数选择

在K-均值的迭代算法中，初始步骤里需要选择均值向量。尽管均值向量的初始化选择可以是随机的，但是其选择会影响模型的迭代性能，其敏感性和随机性造成容易陷入局部最优解和聚类结果波动性大的问题。

解决方法：
选择批次距离尽可能远的K个点
选用层次聚类
注：层次聚类是另一种无监督的聚类方式，它在不同的层次对数据集进行划分，从而形成树形的聚类结构。

聚类个数的选择
理论基础：给定一个合适的类簇指标，比如平均半径或直径，只要我们假设的类簇的数目等于或者高于真实的类簇的数目时，该指标上升会很缓慢，而一旦试图得到少于真实数目的类簇时，该指标会急剧上升。
注：
类簇的直径：类簇内任意两点之间的最大距离。
类簇的半径：类簇内所有点到类簇中心距离的最大值

Elbow方法
作为K-均值模型中的超参，K的选择可以从各种可能的取值中挑选最合适的值。能否选择使得损失函数$E=∑_(𝑖=1)^𝐾 ∑_(𝑥∈𝐶_𝑖) (𝑥−𝜇_𝑖 )^2 $最小的K？
答案是否定的。因为一般来讲K越大则E越小。最极端的情况下，选择与样本量相同的K可以使得损失函数降为0。但此时聚类模型不具有任何意义。Elbow方法可以较好地提供K的估计值。
对于不同的聚类个数K的选择，计算每个K值对应的损失函数的变化趋势。当发现损失函数E在某个K的领域内的变化趋势发生改变时，则可以选择对应的K值。

例如，上图的例子显示E在3个聚类簇时改变了下降趋势，因此可以用3个聚类簇来构建K-Means

二. K邻近分类：近朱者赤、近墨者黑

2.1 K-邻近算法（K-Nearest Neighbors， K-NN）

除了无监督场景外，聚类算法在有监督场景中也有广泛的应用。区别于无监督场景，有监督场景中的算法通常依赖于部分已知标签的样本进行模型构建。
与一般的有监督模型例如回归、决策树等模型不同， K-邻近算法属于基于实例的学习模式。它不会训练一个可以泛化的模型，而是当需要对新样本进行学习时，再将该新样本与已知标签的样本进行分析并给出最后的分类。
K-邻近算法的思想是：对于某待分类样本，通过其邻域样本的分类情况来判断该样本的类别属性。

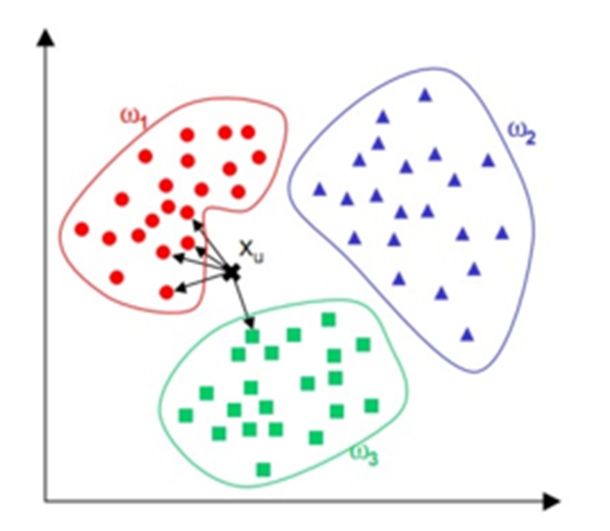
基本的K-邻近算法是非常简单的：

但是实际操作中面临三个问题：
K值的选取
非平衡样本的影响
大样本下的计算开销

2.2 问题

问题一：K值的选取
当K很小的时候，分类结果很不稳定，随机因素会对结果产生较大的影响。 K值较大的时候，离待分类样本较远的样本也会对分类结果产生干扰。最极端的情况即K等于全部已知标签的样本量时，K-邻近模型退化成最简单的形式：无论待分类样本是什么，都会被划分为占比最多的类。那么在K-邻近中应该如何选择K值？
K值的选择办法：通常采用交叉验证法来选取最优的K值。在已知标签的样本上对可能的每一种K值进行留一法（或者其他验证法）验证，平均分类误差最小的K值可以作为K-邻近算法在该训练集上的参数。

问题二：非平衡样本的影响
注意到在K-邻近算法中，待分类样本是以邻近样本中的频率最高的类别作为类别属性。当训练集中的类别数比较均衡时，这样做是合理的。然而在某些场景下，类别的分布并不是均衡的。以信贷金融场景中的欺诈为例，正常样本与欺诈样本的比例可以达到50:1甚至100:1，即所谓的非平衡样本，其中占比较多的类别称为多类，反之称为少类。
可以想像地出来，即使某待分类样本属于少类，由于少类的占比极低，因此在邻近域中的占比也大概率地低于多类样本，使得该待分类样本被划分为多类。可以采用欠采样、过采样等方法解决非平衡样本的问题。

问题三：大样本下的计算开销
假设带标签的训练样本数据的总量为N，则对于M个待分类样本，需要计算其中每一个与N个样本的距离。当N、M较小时，这样做是可以接受的。当N、M很大时，计算开销将会很可观。M是业务决定的数值，但是可以对N进行优化。
考虑到一般情况下K相对N很小，即只有一小部分训练样本会用来决定待分类样本的类别，其他训练样本对最终的结果不会产生影响，那么可以对K-NN过程中的第一步

进行优化。我们不对C中的每一个训练样本计算其与待分类样本的距离，而是对C中的一个子集进行距离计算。寻找这样一个子集的方法通常有KD Tree和 Ball Tree，后者又是对前者的改进。这两种算法都是用来对样本所在的欧式空间进行分割。前者是依赖于超平面的分割，而后者是依赖于超球面的分割。进行分割后，可以极大地减少距离计算需要的样本量。

2.3 K-邻近算法的改进

注意到，在基础的K-邻近算法中，待分类样本将被划分到邻近K个样本中占比最多的类别中，此处K个样本的作用是一样的。

但是我们有理由认为，距离待分类样本更近的训练样本的影响应该更大，也是就是权重应该更高。因此，我们可以用距离的倒数作为K个邻近样本的权重。

三. 案例：信贷客群的聚类分析

在K-均值模型中，我们对数据集中的数值型变量做归一化处理，对类别型变量做独热编码的处理。经过处理，所有变量的取值范围位于[0,1]间。
K-均值模型对K值敏感， 因此我们使用Elbow方法确定K的值，方法如Slide 16所示。在本案例中，K值确定为3.

非平衡样本会对K-邻近算法产生较大的干扰。在本案例中，我们选取5000个违约样本和5000个正常样本构建模型。此外，经过特征工程后数据集中有超过150个变量，这些变量大多具有较强的共线性。共线性的存在意味着信息存在冗余，且高维变量会引起较大的计算量，而大部分变量很可能与目标变量没有相关性，无助于构建模型。因此我们需要进行降维，即减少进入模型的变量。
常用的降维可以有：
1，单变量分析，即检验单个变量的性能再决定挑选哪些变量
2，主成分分析，即将高维变量进行线形组合，使得组合后的新变量线性无关，并且大部分新变量变的不显著，可以移除
3，通过随机森林等集成方法判断变量重要性。本案例中我们选用该方法

在K-邻近算法中，K值的选取也很重要，但是一般无经验可循。我们采用10折交叉验证的方式来进行K的选择：
设定K值的取值空间
对于K的每一种可能的取值，将训练样本随机等分成10份。依次取出其中一份看作无标签样本，与其余的样本构建K-邻近模型，评估准确度，共有10个准确度。取其平均值作为当前K对应的准确度
准确度最高的K值（Best K）可用作本案例中的参数
利用Best K构建K-邻近模型，在测试集上进行测试。结果显示，准确度为60%。

代码:

# -*- coding: utf-8 -*-
"""
Spyder Editor

This is a temporary script file.
"""

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import random
from sklearn import model_selection
from sklearn.cluster import KMeans
from sklearn.neighbors import KNeighborsClassifier
from sklearn.decomposition import PCA
from sklearn.metrics import confusion_matrix
from sklearn.ensemble import RandomForestClassifier


def Outlier(x, k=1.5):
    [lower, upper] = list(np.percentile(x, [25, 75]))
    d = upper - lower
    ceiling = min(max(x), upper + k * d)
    floor = max(min(x), lower - k * d)
    return [floor, ceiling]


def Min_Max_Standardize(x, floor, ceiling):
    d2 = ceiling - floor
    x2 = x.apply(lambda y: max(0, min((ceiling - y) / d2, 1)))
    return x2


def Random_Split(x_list, n):
    '''
    将数列x_list随机等分成n份
    '''
    N = len(x_list)
    random.shuffle(x_list)
    k = int(N / n)
    reminder = N - k * n
    groups = [[j + k * i for j in range(k)] for i in range(n - 1)]
    groups.append(list(range(k * (n - 1), N)))
    random_slice = [[x_list[j] for j in i] for i in groups]
    return random_slice


mydata = pd.read_csv('D:/application_train_small.csv')

cash_loan_data = mydata[mydata['NAME_CONTRACT_TYPE'] == 'Cash loans']
selected_features = ['CODE_GENDER', 'FLAG_OWN_CAR', 'LIVE_CITY_NOT_WORK_CITY', 'ORGANIZATION_TYPE',
                     'FLAG_OWN_REALTY', 'CNT_CHILDREN', 'AMT_INCOME_TOTAL', 'AMT_CREDIT', 'WEEKDAY_APPR_PROCESS_START',
                     'AMT_ANNUITY', 'AMT_GOODS_PRICE', 'NAME_TYPE_SUITE', 'NAME_INCOME_TYPE', 'OCCUPATION_TYPE',
                     'NAME_EDUCATION_TYPE', 'NAME_FAMILY_STATUS', 'NAME_HOUSING_TYPE', 'REGION_POPULATION_RELATIVE',
                     'DAYS_BIRTH', 'DAYS_EMPLOYED', 'DAYS_REGISTRATION', 'DAYS_ID_PUBLISH', 'OWN_CAR_AGE', 'FLAG_MOBIL',
                     'FLAG_EMP_PHONE', 'FLAG_WORK_PHONE', 'FLAG_CONT_MOBILE', 'FLAG_PHONE', 'FLAG_EMAIL',
                     'CNT_FAM_MEMBERS', 'REGION_RATING_CLIENT', 'REGION_RATING_CLIENT_W_CITY',
                     'HOUR_APPR_PROCESS_START', 'REG_REGION_NOT_LIVE_REGION', 'REG_REGION_NOT_WORK_REGION',
                     'LIVE_REGION_NOT_WORK_REGION', 'REG_CITY_NOT_LIVE_CITY', 'REG_CITY_NOT_WORK_CITY']

all_data = cash_loan_data[['TARGET'] + selected_features]

train_data, test_data = model_selection.train_test_split(all_data, test_size=0.3)

#########################
####  2，数据预处理  #####
#########################

# 注意到，变量OWN_CAR_AGE和FLAG_OWN_CAR有对应关系：当FLAG_OWN_CAR='Y'时，OWN_CAR_AGE无缺失，否则OWN_CAR_AGE为有缺失
# 这种缺失机制属于随机缺失。
# 此外，对于非缺失的OWN_CAR_AGE，我们发现有异常值，例如0, 1，2等，无法判断该变量的含义，建议将其删除
selected_features.remove('OWN_CAR_AGE')
del train_data['OWN_CAR_AGE']
# 变量OCCUPATION_TYPE和NAME_TYPE_SUITE属于类别型变量，可用哑变量进行编码
categorical_features = ['CODE_GENDER', 'FLAG_OWN_CAR', 'FLAG_OWN_REALTY', 'NAME_TYPE_SUITE', 'NAME_INCOME_TYPE',
                        'NAME_EDUCATION_TYPE',
                        'NAME_FAMILY_STATUS', 'NAME_HOUSING_TYPE', 'OCCUPATION_TYPE', 'WEEKDAY_APPR_PROCESS_START',
                        'ORGANIZATION_TYPE']
numerical_features = [i for i in selected_features if i not in categorical_features]
train_data_2 = pd.get_dummies(data=train_data, columns=categorical_features)

# 删除AMT_ANNUITY缺失的样本
train_data_2 = train_data_2[~train_data_2['AMT_ANNUITY'].isna()]

#######################
####  3，特征衍生  #####
#######################
train_data_2['credit_to_income'] = train_data_2.apply(lambda x: x['AMT_CREDIT'] / x['AMT_INCOME_TOTAL'], axis=1)
train_data_2['annuity_to_income'] = train_data_2.apply(lambda x: x['AMT_ANNUITY'] / x['AMT_INCOME_TOTAL'], axis=1)
train_data_2['price_to_income'] = train_data_2.apply(lambda x: x['AMT_GOODS_PRICE'] / x['AMT_INCOME_TOTAL'], axis=1)
numerical_features.append('credit_to_income')
numerical_features.append('annuity_to_income')
numerical_features.append('price_to_income')

# 有四个与时长相关的变量DAYS_BIRTH，DAYS_EMPLOYED，DAYS_REGISTRATION	，DAYS_ID_PUBLISH中带有负号，不清楚具体的含义。
# 我们在案例中仍然保留4个变量，但是建议在真实场景中获得字段的真实含义


#####################
####  4，归一化  #####
#####################
# 归一化工作中要考虑到极端值的影响。如果有极端值存在，则需要先排除极端值再做归一化
col_floor_ceiling = {}
for col in numerical_features:
    if min(train_data_2[col]) == 0 and max(train_data_2[col]) == 1:
        continue
    [floor, ceiling] = Outlier(train_data_2[col])
    if ceiling == floor:
        print('{} is a constant variable'.format(col))
        continue
    col_floor_ceiling[col] = [floor, ceiling]
    train_data_2[col] = train_data_2.apply(lambda x: max(0, min((ceiling - x[col]) / (ceiling - floor), 1)), axis=1)

all_features = list(train_data_2.columns)
all_features.remove('TARGET')
X0, y = train_data_2[all_features], train_data_2['TARGET']

###################
##### K-Means #####
###################
elbow = []
for n in range(2, 10):
    Kmeans_model = KMeans(n_clusters=n).fit(X0)
    centres = Kmeans_model.cluster_centers_
    dists_mat = Kmeans_model.transform(X0)
    dists_to_centers = np.min(dists_mat, 1)
    E = sum(dists_to_centers ** 2)
    elbow.append(E)

plt.plot(list(range(2, 10)), elbow)
plt.title('Elbow method for K-Means')

n_best = 3
Best_Kmeans_model = KMeans(n_clusters=n_best).fit(X0)
labels = Best_Kmeans_model.labels_
# sample_labels = np.column_stack((X0, labels))
# label_set = list(set(labels))
# fig, ax = plt.subplots()
# for l in label_set:
#    clusters = sample_labels[sample_labels[:,-1]==l, :]
#    ax.plot(clusters[:50,2], clusters[:50,3], marker='o', linestyle='', ms=12, label=name)
# plt.show()


################
##### K-NN #####
################
X_G, X_B = np.mat(train_data_2[train_data_2['TARGET'] == 0]), np.mat(train_data_2[train_data_2['TARGET'] == 1])
X_G_2, X_B_2 = X_G[:5000, 1:], X_B[:5000, 1:]  # X_G第一列是TARGET，故去掉
X1 = np.vstack([X_G_2, X_B_2])
y_G, y_B = np.zeros(5000), np.ones(5000)
y = np.concatenate((y_G, y_B))

train_index = random.sample(range(10000), 6000)
test_index = [i for i in range(10000) if i not in train_index]

X_train, y_train = X1[train_index, :], y[train_index]
X_test, y_test = X1[test_index, :], y[test_index]

# 将常数列去掉
std = np.std(X_train, axis=0).getA()[0]
constant_index = np.where(std == 0)
X_train = np.delete(X_train, constant_index, axis=1)
X_test = np.delete(X_test, constant_index, axis=1)

###############################
# 先用随机森林的变量重要性进行降维 #
###############################
RFC = RandomForestClassifier().fit(X_train, y_train)
importance = list(RFC.feature_importances_)
index = [i for i in range(X_train.shape[1]) if importance[i] >= 0.01]
X_train_2, X_test_2 = X_train[:, index], X_test[:, index]

###########################
# 也可以用用主成分分析进行降维 #
###########################
pca = PCA(n_components=40)
pca.fit(X_train)
print(sum(pca.explained_variance_ratio_))  # 90%
X_pca_train = pca.fit_transform(X_train)

# 交叉验证法确定K值
fold = 10
K_initial = range(5, 201, 5)
scores_K = []
for K in K_initial:
    X_index = list(range(X_train_2.shape[0]))
    random_split = Random_Split(X_index, fold)
    scores = []
    for valid_set_index in random_split:
        train_set_index = [i for i in X_index if i not in valid_set_index]
        train_set_X, train_set_y = X_train_2[train_set_index, :], y_train[train_set_index]
        valid_set_X, valid_set_y = X_train_2[valid_set_index, :], y_train[valid_set_index]
        neigh = KNeighborsClassifier(n_neighbors=K, algorithm='ball_tree', weights='distance').fit(train_set_X,
                                                                                                   train_set_y)
        # score = neigh.score(valid_set_X, valid_set_y)
        valid_set_y_pred = neigh.predict(valid_set_X)
        cm = confusion_matrix(valid_set_y, valid_set_y_pred)
        score = (cm[0][0] + cm[1][1]) / ((cm[0][0] + cm[1][1]) + cm[0][1] + cm[1][0])
        scores.append(score)
    scores_K.append(np.mean(scores))

K_max_index = scores_K.index(max(scores_K))
Best_K = K_initial[K_max_index]  # 175

K_initial = range(171, 180)
scores_K = []
for K in K_initial:
    X_index = list(range(X_train_2.shape[0]))
    random_split = Random_Split(X_index, fold)
    scores = []
    for valid_set_index in random_split:
        train_set_index = [i for i in X_index if i not in valid_set_index]
        train_set_X, train_set_y = X_train_2[train_set_index, :], y_train[train_set_index]
        valid_set_X, valid_set_y = X_train_2[valid_set_index, :], y_train[valid_set_index]
        neigh = KNeighborsClassifier(n_neighbors=K, algorithm='ball_tree', weights='distance').fit(train_set_X,
                                                                                                   train_set_y)
        # score = neigh.score(valid_set_X, valid_set_y)
        valid_set_y_pred = neigh.predict(valid_set_X)
        cm = confusion_matrix(valid_set_y, valid_set_y_pred)
        score = (cm[0][0] + cm[1][1]) / ((cm[0][0] + cm[1][1]) + cm[0][1] + cm[1][0])
        scores.append(score)
    scores_K.append(np.mean(scores))

K_max_index = scores_K.index(max(scores_K))
Best_K = K_initial[K_max_index]  # 178

best_neigh = KNeighborsClassifier(n_neighbors=Best_K, algorithm='ball_tree', weights='distance').fit(X_train_2, y_train)
y_test_pred = best_neigh.predict(X_test_2)
cm = confusion_matrix(y_test, y_test_pred)
score = (cm[0][0] + cm[1][1]) / ((cm[0][0] + cm[1][1]) + cm[0][1] + cm[1][0])
print(score)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232

测试记录：

0.5915
1

参考:

1. http://www.dataguru.cn/mycourse.php?mod=intro&lessonid=1701