• 神经网络（三）分类器与线性模型

    一、线性分类

            线性分类器：属于监督学习

            1.线性分类模型

                                   

                            f(x;w)称判别函数，因其由一根直线将平面划分成两份，所以称线性分类模型

                             线性分类模型 = 线性判别函数 + 线性决策边界

            2.二分类问题

                    ①模型

                     ②损失函数

                            0-1损失函数：L_{01}(y,g(f(x;w)))=I(y\neq g(f(x;w))) （判定是否正确，但是不能求导）

            3.多分类问题

                    ①模型

                             a)一对其余：转换为多个二分类。有几类需要构建几种分类器，但是交叉区域可能才出现未知。

                             b)一对一：每两个类之间建立分类器（\frac{c(c-1)}{2}个分类器），采用投票的方式决定分类。同样存在不明的交叉区域（略小），且对于多中分类过于复杂。

                             c)argmax：对一对其余的改进，由其在各区域得分作为分类依据（分数最高）

                                    预测函数：y=argmax_{c=1}^Cf_c(x;w_c)

     二、交叉熵与对数似然

            1.交叉熵

                    熵：用以衡量一个随机事件的不确定性，熵↑，随机信息越多（干扰信息）

                    自信息：一个随机时间包含的信息量        I(x) =-log p(x)

                    熵可以描述为：随机变量X的自信息的数学期望

                            其分布为：H(X)=E_X[-log p(x)]=-\sum_{x\in X}p(x)logp(x) 

                    熵编码：在对分布p(y)的符号进行编码时，熵H(p)也是理论上最优的平均编码长度

                    交叉熵：按照概率分布q的最优编码对真实分布为p的信息进行编码的长度。

                            H(p,q)=E_p[-logq(x)]=-\sum_xp(x)logq(x)

                            在给定q的情况下，若p和q越接近，交叉熵越小

                    KL散度：用概率分布q来近似p时所造成的信息损失量

                            KL(p,q)=H(p,q)-H(p)=\sum_xp(x)log\frac{p(x)}{q(x)}

            2.对数似然

                    交叉熵在机器学习的应用

                    真实分布p_r(y|x)        预测分布p_\theta (y|x)

                    KL(P_r(y|x),p_\theta(y|x))=\sum_yP_r(y|x)log \frac{P_r(y|x)}{p_\theta(y|x)}             KL散度

                                                            \propto -\sum_yP_r(y|x)logp_ \theta(y|x)        交叉熵损失

                                                            =-logp_\theta(y^*|x)                          负对数似然

    三、Logistic回归

            ①模型

             ②损失函数

                    将分类问题看作条件概率估计问题，通过引入激活函数g，将线性函数f转换为概率

                            以二分类为例，问题将会变为估测两个概率p_\theta(y=1|x) 和p_\theta(y=0|x)

                            激活函数g：将线性函数的值域挤压到(0,1)之间，以表示概率。

            ③Logistic函数

                     Logistic回归：p_\theta(y=1|x)=\sigma(w^Tx)=\frac{1}{1+exp(-w^Tx)}

            ④学习准则

                    预测条件概率：p_\theta(y=1|x)=\frac{1}{1+exp(-w^Tx)}

                    真实条件概率：p_r(y=1|x)=y^*        p_r(y=0|x)=1-y^*

                    交叉熵：H(p_r,p_\theta)=-(y^*log\hat{y}+(1-y^*)log(1-\hat{y}))

                    梯度下降：

                            风险函数：R(w)=-\frac{1}{N}\sum_{n=1}^N(H(p_r,p_\theta)) 交叉熵的平均值的负数

                            梯度：对风险函数求导->\frac{\partial R(w)}{\partial w}=-\frac{1}{N}\sum_{n=1}^Nx^{(n)}(y^{(n)}-\hat{y}^{(n)})

                            迭代更新：w_{t+1}\leftarrow w_t+\alpha \frac{1}{N}\sum_{n=1}^Nx^{(n)}(y^{(n)}-\hat{y}_{w^t}^{(n)})

    四、Softmax回归

             应用于多分类问题

            ①模型

             ②学习准则

                    转换为条件概率建模：p_\theta(y=c|x)

            ③Softnax函数

                    对于K个标量x1,...xk        softmax(x_k)=\frac{exp(x_k)}{\sum_{i=1}^{K}exp(x_i)}

             ④Softmax回归

                    p_\theta(y=c|x)=\frac{exp(w^T_cx)}{\sum^C_{({c}'=1)}exp(w^T_{}c'x)} 

                            向量表示：​​​​​​​

             ⑤交叉熵损失

                             向量表示：-\hat ylog \hat y

            ⑥学习准则

                    风险函数：R(w)=-\frac{1}{N}\sum^N_{n=1}(y^{(n)})^Tlog\hat y^{(n)}

                    梯度下降：

     五、感知器

            ①模型

                    模拟生物神经元行为，包含权重(突出)、偏置(阈值)、激活函数(细胞体)，输出结果为+1或-1

                    y=sgn(w^Tx)

                     类似于Logistic函数

            ②学习目标

                    找到权重 w^* 使得 y^{(n)}w^{*T}x^{(n)}>0

            ③学习方法

                    错误驱动的在线学习算法。

                    1.初始化一个权重向量w<-0（一般为零向量）

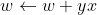
                    2.每次分错一个样本(x,y)时，即yw^Tx<0，则使用这个样本来更新权重w\leftarrow w+yx

            ④损失函数

                    由错误驱动的在线学习算法反推得到\frac{\partial R(w)}{\partial w}=-yx        (不更新时为0)

                            L(w;x,y)=max(0,-yw^Tx)

            ⑤学习过程

             ⑥收敛性

                    对于给定的训练集D且线性可分，令R是训练集中最大的特征向量的模，即R=max||x^{(n)}||，感知器使用错误驱动在线学习算法时权重更新次数不超过\frac{R^2}{\gamma ^2}

    六、支持向量机

            ①最大间隔

                    间隔：决策边界到分类样本的最短距离

             ②支持向量机

                    点x^{(n)}到超平面的距离：\gamma ^{(n)}=\frac{y^{(n)}(w^Tx^{(n)}+b)}{||w||}

                    支持向量机的目的是寻找一个超平面使得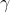\gamma 最大

             ③软间隔

                    为了容忍部分不满足约束的样本，可以引入松弛变量

                    原式：y^{(n)}(w^Tx^{(n)}+b)\geq 1

                    转换为：y^{(n)}(w^Tx^{(n)}+b)\geq 1-\xi _n

            ④损失函数

                    L_p=max(0,-yf(x;w))

    七、小结

  • 相关阅读:
    深入URP之Shader篇1: URP Shader概述
    小型气象站数据采集网关准确监测雨量和风速
    Python 之plt.plot()的介绍以及使用
    【Web基础篇】Servlet原理
    "嫦娥奔月"，难道古人早已看透一切？
    Dataset 的基础知识和RDD转换为DataFrame
    【网络安全】网络安全基础精讲 - 网络安全入门第一篇
    android 布局 横屏 android横屏适配
    Docker从认识到实践再到底层原理（六-2）｜Docker容器操作实例
    Spring Boot 各版本的支持时间
  • 原文地址：https://blog.csdn.net/weixin_37878740/article/details/126378495