1. 邻接矩阵

1.1 邻接矩阵结构体

//vertex是顶点的意思
#define MaxVertexNum 100	//顶点数目的最大值

typedef struct{
    char Vex[MaxVertexNum];		//顶点表【存A、B、C、D...】
    int Edge[MaxVertexNum][MaxVertexNum];	//邻接矩阵，边表【全是0或1】
    int vexnum,arcnum;			//图的顶点数和边数
}MGraph;
1
2
3
4
5
6
7
8

注：圆括号是无向图，尖括号是有向图
 
无向图：
第i个结点的度 = 第 i 行（或第i列）的非零元素个数
有向图：

①出度：第 i 行的非零元素个数；
②入度：第 i 列的非零元素个数。
度：第 i 个结点的度 = ① + ②

【邻接矩阵法】存储带权图（网）：

#define MaxVertexNum 100		//顶点数目的最大值
#define INFINITY 2147483647;	//表示“无穷”

typedef char VertexType;	//顶点数据类型
typedef int EdgeType;		//边数据类型

typedef struct{
    VertexType Vex[MaxVertexNum];	//顶点表
    EdgeType Edge[MaxVertexNum][MaxVertexNum];	//边的权值
    int vexnum,arcnum;		//图的当前顶点数和弧数
}MGraph;
1
2
3
4
5
6
7
8
9
10
11

1.2 时间和空间复杂度

【求（无向图）顶点的度、（有向图）出度/入度】的时间复杂度为 O(|V|)
空间复杂度：O(|V|²) ——只和顶点数相关，和实际的边数无关
适合用于存储稠密图

1.3 邻接矩阵相乘的意义

如：

---

2. 邻接表

2.1 邻接表结构体

存储无向图、有向图：

#define MVNum 100							//最大顶点数

typedef struct ArcNode{                		//边/弧 
    int adjvex;                             //邻接点的位置 【0、1、2、3、4...】
    struct ArcNode *next;	      			//指向下一个表结点的指针 
}ArcNode;


typedef struct VNode{ 
    char data;                    	        //顶点信息【存A、B、C、D...】
    ArcNode *first;         				//第一条边/弧 
}VNode, AdjList[MVNum];                 	//AdjList表示邻接表类型 


typedef struct{ 
    AdjList vertices;              			//头结点数组
    int vexnum, arcnum;     				//当前的顶点数和边数 
}ALGraph; 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

  
  
该图中的顺序可以是321或其他，也就是不唯一

2.2 时间和空间复杂度

数组的大小是|V|，边结点的数量是2|E|——>整体空间复杂度为O(|V| + 2|E|)

---

----------------------------邻接矩阵和邻接表的区别

---

3. 十字链表【只存储有向图】

#define MAX_VERTEX_NUM 20	//最大顶点数量

typedef struct ArcBox{		//弧结点
	int tailvex, headvex;	//弧尾，弧头顶点编号（一维数组下标）
	struct ArcBox *hlink, *tlink;	//弧头相同、弧尾相同的下一条弧的链域
	InfoType info;			//权值
}ArcBox;

typedef struct VexNode{		//顶点结点
	VertexType data;		//顶点数据域
	ArcBox *firstin, *firstout;	//该顶点的第一条入弧和第一条出弧
}VexNode;

typedef struct{				//有向图
	VexNode xlist[MAX_VERTEX_NUM];	//存储顶点的一维数组
	int vexnum, arcnum;	//有向图的当前顶点数和弧数
}OLGraph;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

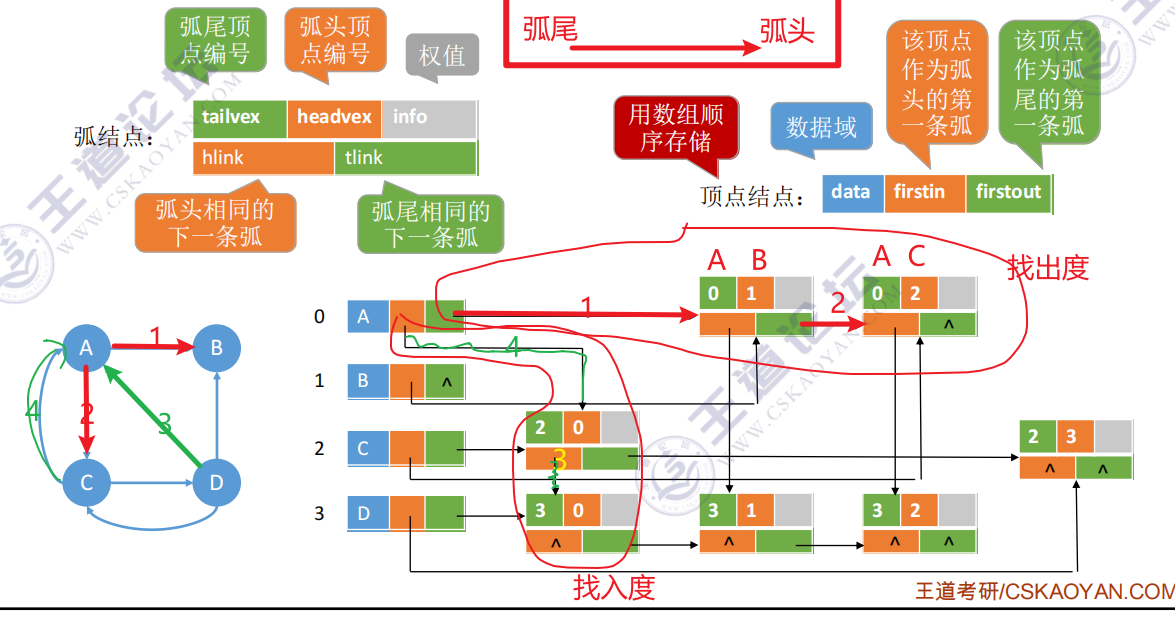
空间复杂度：O(|V|+|E|)

如何找到指定顶点的所有出边？——顺着绿色线路找
如何找到指定顶点的所有入边？——顺着橙色线路找

注意：十字链表只用于存储有向图

---

4. 邻接多重表【只存储无向图】

#define MAX_VERTEX_NUM 20	//最大顶点数量

struct EBox{				//边结点
	int i,j; 				//该边依附的两个顶点的位置（一维数组下标）
	EBox *ilink,*jlink; 	//分别指向依附这两个顶点的下一条边
	InfoType info; 			//边的权值
};
struct VexBox{
	VertexType data;
	EBox *firstedge; 		//指向第一条依附该顶点的边
};
struct AMLGraph{
	VexBox adjmulist[MAX_VERTEX_NUM];
	int vexnum,edgenum; 	//无向图的当前顶点数和边数
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

空间复杂度：O(|V|+|E|)【因为：每条边只对应一份数据】
删除边、删除节点等操作很方便
注意：只适用于存储无向图

---

-----------------------邻接矩阵、邻接表 、十字链表 、邻接多重表【区别】