NR 物理层 狄拉克函数3 狄拉克傅里叶变换深度剖析

参考：

        Explains why the Fourier transform of a sum of delta impulse functions is also a sum of delta impulse functions, but in the frequency domain. Intuitively it might seem like the Fourier transform should be a constant in the frequency domain, since the transform of a single delta function is a constant. But it doesn't work out like that.

     

前言：

         这篇10分钟左右的课程深入的剖析抽样函数的傅里叶变换.

 目录：

      1：  问题

      2：  相位谱解释

---

一  问题

      

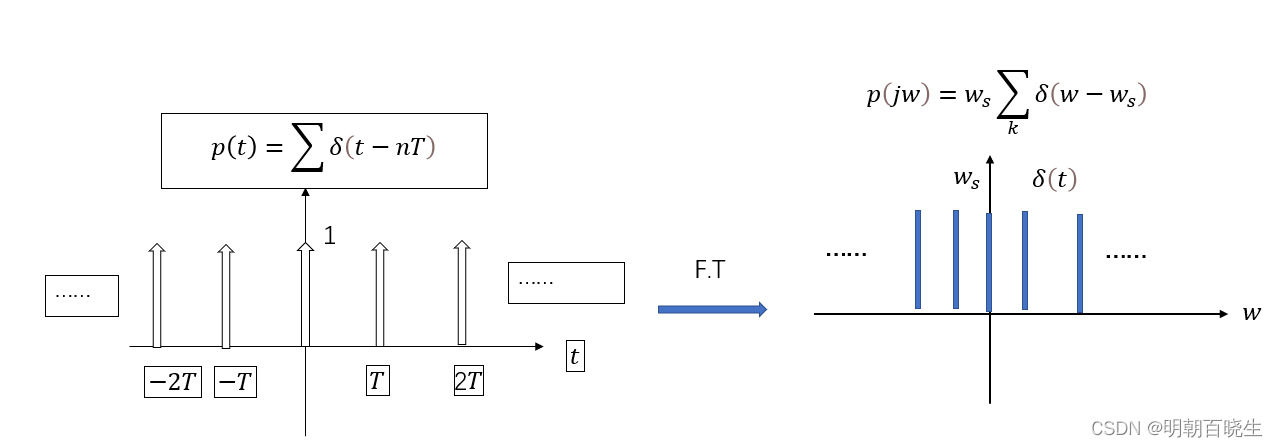
          前面我们知道抽样函数的傅里叶变换为

           

    这个有点违反直觉(why is it counter- intuitive?)

  我们前面知道单独一个狄拉克函数傅里叶变换是一个常数（flat functions)抽样函数是很多

狄拉克函数的线性和，其傅里叶变换也应该是很多常数的线性和,而不是脉冲串,这个就是

很多人的疑惑点，违反直觉。

---

二  相位谱解释

     产生上述原因，主要是我们忽略了相位谱。

   这里结合主要结合相位谱,讨论为什么w 一定要取的整数倍

主要原理： contribution to the fourier transform at that freqeuency

   

  2.1 n =0,

      傅里叶变换后相位为0

    

  相位   

 2.2  n=1 

   ,傅里叶变换后相位为-wT

    

   

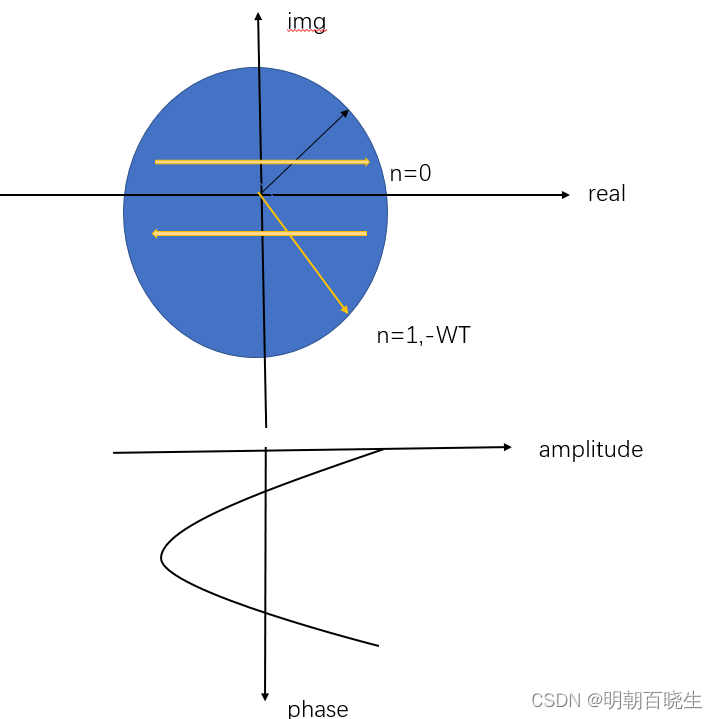
这里面固定T,讨论W:

     因为是一个复数，我们可以用一个圆来表示，x坐标轴表示实部，y坐标轴表示虚部。

我们从下面图中可以看到虚部，因为w 从负无穷到正无穷，所以相位总是有个相反的相位，

所以虚部投影可以不考虑，被对消了

只考虑在real坐标轴上面的投影：

         相当于随着w变化，先减小再增大，周期性变化

固定w,考虑几个特殊情况

1  

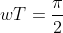
  抽样信号傅里叶变换后,其只有4种相位, 叠加后实部 虚部和都为0

 zero contribution to the fourier transform at that frequency .

  

2 

  同样

 zero contribution to the fourier transform at that frequency .

 

3 

 , 这个时候其和就不是0了，是一个常数，所以

w 必须等于 

 

4  

 因为抽样信号n从负无穷到正无穷,所以最后傅里叶变换后,整个可以对消掉。

  add up all the contributions ,they all cancel.