1 直方图

1.0 数据集

import seaborn as sns
penguins = sns.load_dataset("penguins")
penguins

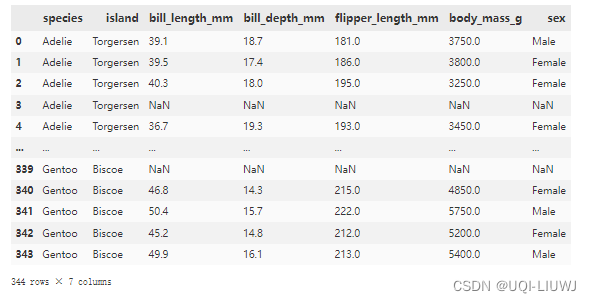
1.1  单变量直方图

1.1.1 displot

sns.displot(penguins, x="flipper_length_mm")

1.1.2  histplot

sns.histplot(penguins, x="flipper_length_mm")

 1.1.3 binwidth 设置直方图间隔宽度

sns.displot(penguins, x="flipper_length_mm",
           binwidth=1)

 

sns.histplot(penguins, x="flipper_length_mm",
            binwidth=10)

 1.1.4 数据类别少的情况

tips = sns.load_dataset("tips")
tips

此时类别只有几个，所以直方图的话画出来没法撑满整张图

sns.displot(tips, x="size")

 

有以下几种解决方法：

1.1.4.1 手动设置bin集合

sns.displot(tips, x="size",bins=[1,2,3,4,5,6,7])

 

1.1.4.2  设置discrete

sns.displot(tips, x="size",discrete=True)

 1.1.4.3 设置shrink

sns.displot(tips, x="size",shrink=2)

 1.5 直方图+hue

sns.displot(penguins, x="flipper_length_mm", 
            hue="species")

1.5.1 element='step'

        默认情况下，不同的直方图相互“分层”，在某些情况下，它们可能难以区分。

         一种选择是将直方图的视觉表示从条形图更改为阶梯图： 

sns.displot(penguins, x="flipper_length_mm", hue="species",
           element='step')

 1.5.2 multiple="stack" （纵向叠加）

不重叠，改为叠加

sns.displot(penguins, x="flipper_length_mm", hue="species",
           multiple='stack')

 1.5.3 multiple="dodge" （横向并列）

sns.displot(penguins, x="flipper_length_mm", hue="species",
           multiple='dodge')

1.6 直方图+col

多张图

sns.displot(penguins, x="flipper_length_mm", 
            col="species")

 

2  核密度估计

• 直方图旨在通过分箱和计数观察来近似生成数据的潜在概率密度函数。 核密度估计 (KDE) 为同一问题提供了不同的解决方案。
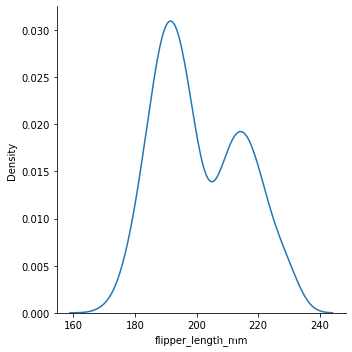
• KDE 图不是使用离散箱，而是使用高斯核平滑观察，产生连续的密度估计：

sns.displot(penguins, x="flipper_length_mm",
            kind="kde")

 2.1 选择平滑带宽

• 与直方图中的 bin 大小非常相似，KDE 准确表示数据的能力取决于平滑带宽的选择。
• 过度平滑的估计可能会删除有意义的特征，但平滑不足的估计会掩盖随机噪声中的真实形状。
• 检查估计的稳健性的最简单方法是调整默认带宽

sns.displot(penguins, x="flipper_length_mm",kind="kde",
           bw_adjust=.05)

sns.displot(penguins, x="flipper_length_mm",kind="kde",
           bw_adjust=.85)

 

2.2 hue

sns.displot(penguins, x="flipper_length_mm",kind="kde",
           hue="species")

 

 2.3 multiple

sns.displot(penguins, x="flipper_length_mm",kind="kde",hue="species",
            multiple='stack')

 3 累积分布函数

sns.displot(penguins, x="flipper_length_mm",
            kind="ecdf")

 3.1 hue

sns.displot(penguins, x="flipper_length_mm",kind="ecdf",
           hue='species')

 4 双变量分布

4.1 双变量直方图

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm")

4.1.1 颜色-数值 对应图

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm",
            cbar=True)

 

 4.1.2 rug

在图内显示各个独立的观测 

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm",
            rug=True)

 

 4.2 双变量等高线

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm",
           kind='kde')

4.2.1 thresh——最低数值

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm",kind='kde',
           thresh=0.5)

 

4.2.2 levels 几层等高线/手动设置层对应数值

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm",kind='kde',
           thresh=0.5, levels=3)

 

 

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm",kind='kde',
           thresh=0.5, levels=[0.01,0.1,1])

 

 4.2.3 rug

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm",kind='kde',
            rug=True)

  

 4.3 hue

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm",
           hue='species')

 

 

sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm",
           kind='kde',hue='species')

5 联合画图

默认情况下，是2D散点图+各自直方图

sns.jointplot(data=penguins, x="bill_length_mm", y="bill_depth_mm")

 5.1 KDE

sns.jointplot(data=penguins, x="bill_length_mm", y="bill_depth_mm",
             kind='kde')

 5.2 随心配

g = sns.JointGrid(data=penguins, x="bill_length_mm", y="bill_depth_mm")
g.plot_joint(sns.histplot)
g.plot_marginals(sns.boxplot)

plot_joint——中间的图

plot_marginals——两边的图

 5.3 pairplot

我们再回顾一下这个数据集

import seaborn as sns
penguins = sns.load_dataset("penguins")
penguins

有四个有数据的列，我们用pairplot之后，对角线部分是数值的直方图。非对角线部分是散点图

sns.pairplot(penguins)

 

5.3.1 随心配

g = sns.PairGrid(penguins)
g.map_upper(sns.histplot)
g.map_lower(sns.kdeplot)
g.map_diag(sns.histplot, kde=True)

参考内容 Visualizing distributions of data — seaborn 0.11.2 documentation (pydata.org)