回归定义

Regression就是找到一个函数 function，通过输入特征 xxx，输出一个数值 Scalar。

应用举例

股市预测（Stock market forecast）
输入：过去10年股票的变动、新闻咨询、公司并购咨询等
输出：预测股市明天的平均值
自动驾驶（Self-driving Car）
输入：无人车上的各个sensor的数据，例如路况、测出的车距等
输出：方向盘的角度
商品推荐（Recommendation）
输入：商品A的特性，商品B的特性
输出：购买商品B的可能性
宝可梦攻击力预测（Combat Power of a pokemon）：
输入：一只宝可梦（X）的特征：X_cp进化前的CP值、X_s物种（Bulbasaur）、X_hp血量（HP）、X_w重量（Weight）、X_h高度（Height）
输出：进化后的CP值【f(X)=y】

模型步骤

step1：模型假设，选择模型框架（线性模型）
step2：模型评估，如何判断众多模型的好坏（损失函数）
step3：模型优化，如何筛选最优的模型（梯度下降）
1
2
3

以宝可梦问题举例的线性模型

模型假设（线性模型）

b,w可以是任意实值，因此function set中可以有无穷无尽的function，但根据常识及已知条件也可以判断某些function是不可能成立的。
又由于输入特征的多样性，故得到多元线性模型如上
x_i各类特征，w_i各个特征的权重，b偏移量

模型评估——损失函数

收集和查看训练数据

定义 x¹ 是进化前的CP值，${\hat{y}}^1$ 进化后的CP值，$\hat{}$ 所代表的是真实值

评估模型的好坏——loss function

loss function:对function做出评估
举例：均方误差如上

模型优化——筛选最优模型（梯度下降）

已知损失函数是 L(w,b)如上，需要找到一个令结果最小的f^*,在实际的场景中，我们遇到的参数肯定不止w,b。

梯度下降法

先从最简单的只有一个参数w的损失函数入手，定义$w^{\ast }=arg\underset{x}{\min }L(w)$

先随机选取一个初始点w⁰,在该点计算参数w对loss function的微分（切线斜率）：

• 如果斜率为负，直观可知最小值点在该点右侧，因此增加w值
• 如果斜率为正，减小w值，使loss减少

增加值大小通过计算$-\eta \frac{dL}{dw}{|}_{w=w^0}$得到，其中有两个决定性因素：学习率（移动的步长）$\eta$和该点处斜率值

重复上述步骤，直到找到最低点
但是找到的可能是局部最低点（回归中不会出现该问题）

两参数情况——计算偏微分

梯度下降的可视化

每一条线围成的圈就是等高线，代表损失函数的值，颜色越深的区域代表的损失函数越小
红色的箭头代表等高线的法线方向，也就是学习过程前进的方向

梯度下降算法在现实世界中面临的挑战
问题1：当前最优（Stuck at local minima）
问题2：等于0（Stuck at saddle point）
问题3：趋近于0（Very slow at the plateau）

步骤优化

通过对 Pokemons种类 判断，将 4个线性模型 合并到一个线性模型中

加入更多特征
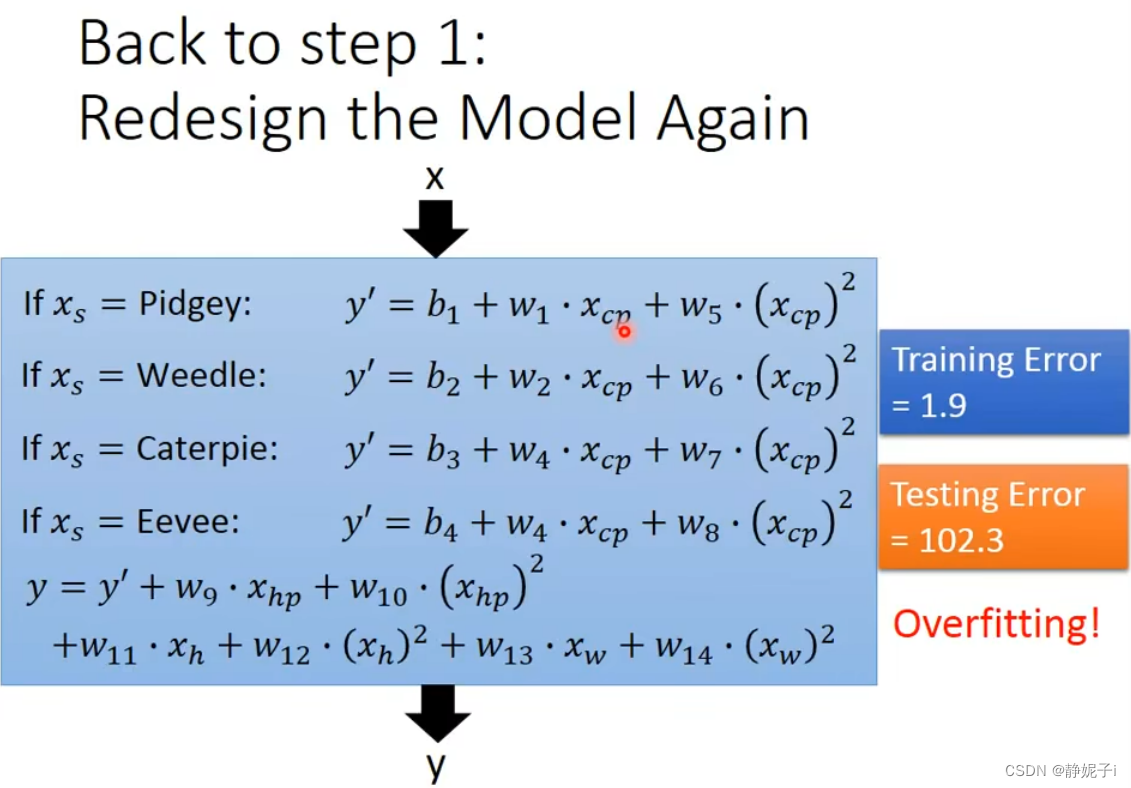更多特征，更多input，数据量没有明显增加，仍旧导致overfitting
（在训练集上面表现更为优秀的模型，为什么在测试集上效果反而变差了？这就是模型在训练集上过拟合的问题）

加入正则化

w 越小，表示 function较平滑的， function输出值与输入值相差不大
在很多应用场景中，并不是 w 越小模型越平滑越好，但是经验值告诉我们 w 越小大部分情况下都是好的。
b(bias)的值接近于0 ，对曲线平滑(上下移动)是没有影响