java基础学习笔记—— 基础语法篇

记录一下这些天学习的一些关于JavaSE的基础, 因为之前有一些语法基础，所以语法部分笔记不是很完整。

前言

一、特性和优势

简单性、面向对象、可移植性、高性能、分布式、动态性、多线程、安全性、健壮性

Write Once、 Run Anywhere

二、JDK、JRE、 JVM

• JDK: Java Development Kit

• JRE: Java Runtime Environment

• JVM: Java Virtual Machine

  JDK = JRE + 开发工具集(如Javac编译工具等)

  JRE = JVM + Java SE 标准类库

三、程序运行机制

• 编译型 和 解释型
  

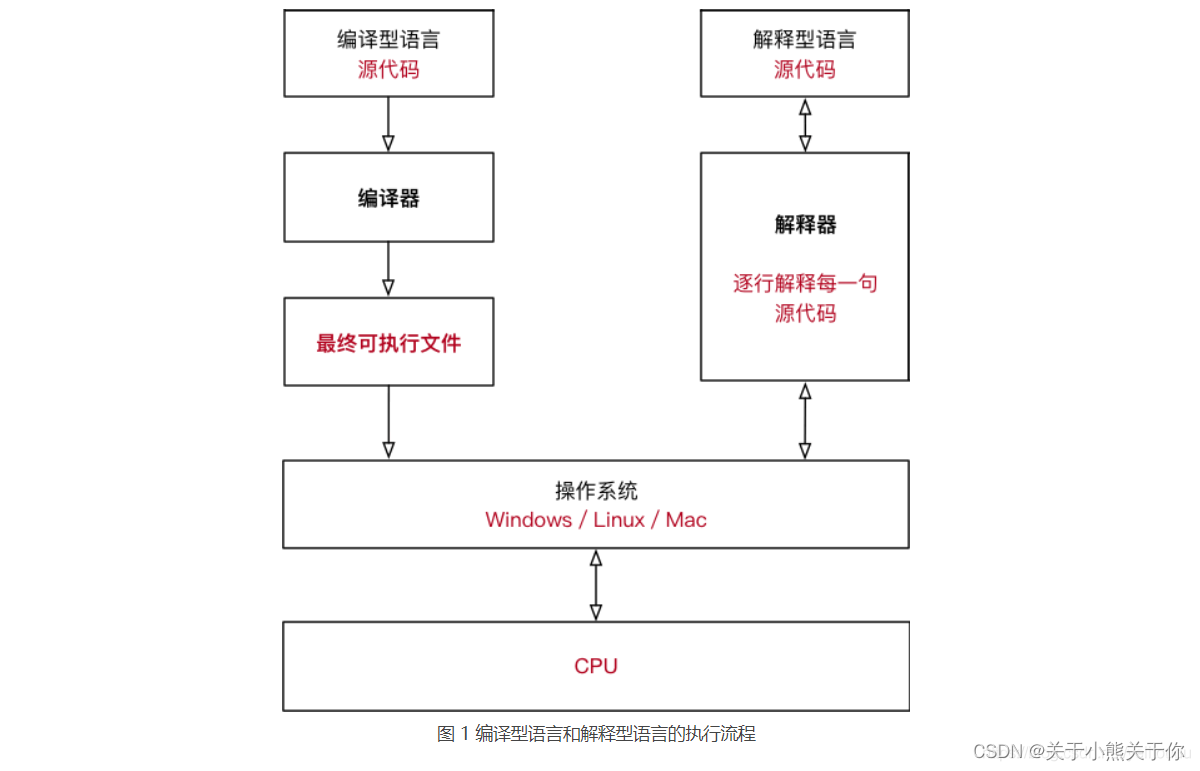
• 程序运行机制
  

• 核心机制------ 垃圾回收

四、内存分析

语法(部分)

一、数据类型

• java是强类型语言

• 基本类型（primitive type）
  

• 引用类型（reference type）

  • 类(如String)
  • 接口
  • 数组

引用类型比较是比较地址

整数扩展

浮点数扩展

• float 有限 、 离散 、 舍入误差 、 大约 、 接近但不等于

• double

  单精度数7位有效数字，尾数用23位存储。 （float）
  双精度数16位有效数字，尾数用52位存储。（double）

浮点数比较问题

最好完全避免使用浮点数进行比较, 由于精度问题，直接比较有时可能会出错。

使用BigDecimal 数学工具类

float f = 0.1f;  //0.1
double d = 1.0/10;  //0.1
> f==d
> false    //精度不同
    
float d1 = 232313213412343232f;
float d2 = d1 + 1;
> d1==d2
>true    //一个超出表示范围的大数，再加一后。此时加一很有可能被截断。

1
2
3
4
5
6
7
8
9
10

浮点数表示

$$\begin{gathered} N=M\times R^E \\ 如：12.345=1.2345\times 10^1 \\ 其中，M为浮点数的尾数，R为阶码的基数，E为阶的阶码 \end{gathered}$$

浮点数表示：

• 要给出尾数M的值，通常用定点小数形式表示，它决定了浮点数的表示精度，即可以给出的有效数字的位数；
• 要给出阶码，通常用定点整数形式表示，它指出的是小数点在数据中的位置，决定了浮点数的表示范围；

假定为32位浮点数，基为2，其中最高位为符号位

浮点数的规格化表示

为了提高数据的表示精度同时保证数据表示的唯一性，需要对浮点数做规格化处理

在计算机内，对非0值的浮点数，要求尾数的绝对值必须大于基数的倒数，即$|M|>=\frac{1}{R}$

即要求尾数域的最高有效位应为1,称满足这种表示要求的浮点数为规格化表示

正数 0.1xxxxxx

负数 1.1xxxxxx

注意，尾数的最高位始终是1，因此我们完全可以省略掉该位。

(1). 尾数用原码,且隐藏尾数最高位

​ 原码非0值浮点数的尾数数值最高位必定为 1，因此可以忽略掉该位,这样用同样多的位数就能多存一位二进 制数，有利于提高数据表示精度，称这种处理方案使用了隐藏位技术。当然，在取回这样的浮点数到运算 器执行运算时，必须先恢复该隐藏位。

(2). 阶码使用“移码”，基固定为2

从最高位依次是符号位、阶码和尾数

一个规格化的32位浮点数ｘ的真值为：$x=(-1{)}^s\times (1.M)\times 2^{E-127}$

一个规格化的64位浮点数ｘ的真值为：$x=(-1{)}^s\times (1.M)\times 2^{E-1023}$

1. 浮点数存储时,按照符号，指数，位数进行存储，IEEE754标准，没有办法使用二进制进行精确表示。
2. 单精度数7位有效数字，双精度数16位有效数字
3. 在存储时，会先将十进制数转换成对应的二进制小数，然后将小数点移至尾数前为1的最左边，此时如果数太大时，小数点左移动大，科学计数法指数变大，尾数变多。当尾数太大，超过float或者double尾数表示范围时，将要做截断操作。

二、类型转换

转换时可能存在内存溢出，精度问题

低 -------------------------------------------------- > 高

byte，short,char -> int ->long -> float -> double

• 强制类型转换

  （类型）变量名 高 -> 低

• 自动类型转换

  低 -> 高

三、变量

• 局部变量

​ 必须声明和初始化值，在方法内

• 类变量
  • 成员变量
  • 方法局部变量
  • 静态变量
    如果不初始化，默认值为 0 、0.0 ，布尔值默认为false， 除了基本类型，其余都默认为null；

public class Main{
   int x = 20;//成员变量
   static int y = 30; // 静态变量，随着类的加载而加载
   public int wrong() { 
      int i; // 方法局部变量
      return i+5;
    } 
    
}
1
2
3
4
5
6
7
8
9

• 常量

  • 初始化后不能再改变值，不会变动的值；

  • 一般使用大写字符, 使用final关键字定义；

  static final PI = 3.1415926;
  1

四、位运算

左移：<<   * 2    右移：>>   / 2

---