论文详解 GLENet 增强型3D目标检测网络

在这里插入图片描述图 1：(a) 给定一个不完整 LiDAR 观测的对象，可能存在多个具有不同大小和形状的潜在合理的真实边界框。 (b) 当注释来自 2D 图像和部分点时，标签过程中的模糊和不准确是不可避免的。在给定的情况下，只有后部的汽车类别的类似点云可以用不同长度的不同真实值框进行注释，长度Length有非常明显的变化。

在上述现象的推动下，还存在另一类概率检测器，它们明确考虑了标签模糊性的潜在影响。最后，这些方法可以分为两种范式，如图 2 所示，(b)范式倾向于输出边界框的概率分布，而不是直接以确定的方式回归确定的框坐标。例如，在高斯分布的假设下，检测头据此预测分布的均值和方差。为了监督这种概率模型，这些工作只是将真实边界框视为Dirac增量分布，然后在估计分布和真实值之间应用 KL 散度。

注：KL散度的概念来源于概率论和信息论中。KL散度又被称为：相对熵、互熵、鉴别信息。在机器学习、深度学习领域中，KL散度被广泛运用于变分自编码器中、EM算法、GAN网络中。在统计学意义上来说，KL散度可以用来衡量两个分布之间的差异程度。若两者差异越小，KL散度越小，反之亦反。当两分布一致时，其KL散度为0。正是因为其可以衡量两个分布之间的差异，所以在VAE、EM、GAN中均有使用到KL散度。

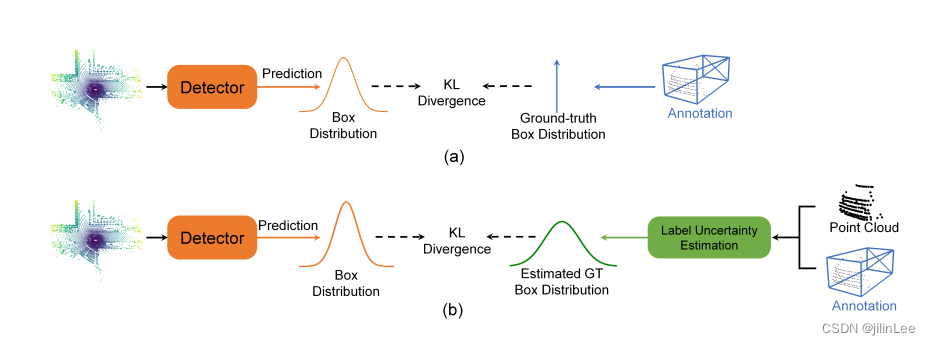在这里插入图片描述图 2：概

相关阅读:
aiops时代, 10分钟学会用AIAnsbile去调试ansible任务
文章投稿经历
spring boot整合 Redis
DependencyProperty.Register：wpf 向别的xaml传递参数
【深度学习】图像超分实验：SRCNN/FSRCNN
C++类和对象（二）构造函数、析构函数、拷贝构造函数
2006-2019年全国30省绿色创新效率、绿色投资效率：基于SBM-DEA测算面板数据（数据+Stata代码）
JavaScript与jQuery（上篇）
javaScript：鼠标事件
（c语言）两个int(32位)整数m和n的二进制表达中，有多少个位(bit)不同

原文地址：https://blog.csdn.net/puiopp63/article/details/126346787