Leetcode 1124. 表现良好的最长时间段

前几日做了DJ的笔试，这个题没有做出来，这两天看了看。分享一下

1.题目链接

 Leetcode1124 

2.题目描述 

3.思路

    这道题在leetcode上面的思路，基本上是使用前缀和+暴力求解，或者是前缀和+单调栈，这两种方法都有理解的前置要求，得先知道前缀和以及单调栈是什么。下面我来介绍一下，搞懂了这两个是什么，有什么用，理解起来就不难了。

   3.1前缀和

     前缀和，即preSum，其实就是从数组中的第 0 位置开始累加，到第 i位置的累加结果，我们常把这个结果保存到数组 preSum 中，记为 preSum[i]。

  公式：preSum[i] = preSum[i - 1] + nums[i]

   从公式中可以看出，前缀和这种计算方式巧妙地利用了以前计算出的结果，比如要计算preSum[3],只需要知道preSum[2]以及nums[3]即可，因为preSum[2]已经保存了从nums[0]到nums[2]相加的结果。

  

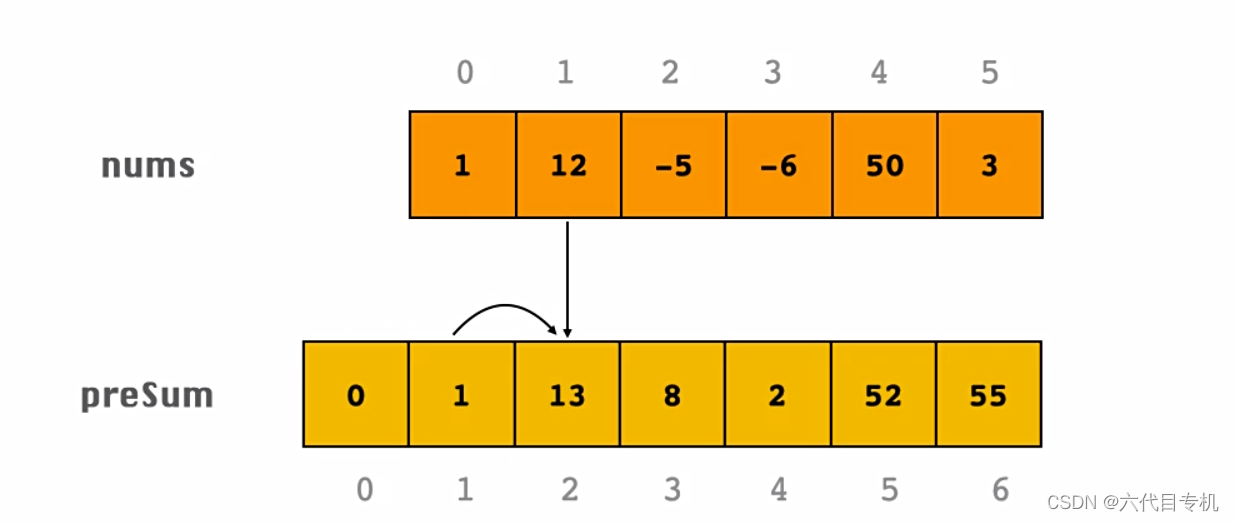
                                                               图1-1 前缀和求解过程

   我们常常把「前缀和」数组 preSum 的长度定义为原数组的长度 + 1。preSum 的第 0 个位置，相当于一个占位符，置为 0。是因为防止越界，因为公式中是preSum[i-1]如果前面没有这个0，会产生越界的错误。

  那么就可以把 preSum 的公式统一为 preSum[i] = preSum[i - 1] + nums[i - 1]，此时的 preSum[i] 表示 nums 中 i元素左边所有元素之和（不包含当前元素 i。）

  3.2前缀和的作用

1.       求解数组前i个数之和，按照定义，比如nums 数组中的前 2 个数的和，就是preSum[2]
2.       求数组的区间和，这个作用在这个算法中会用到，我们利用前缀和数组可以快速求出nums数组[i,j]区间内的元素和，先给出公式。

            

         原理其实很好理解，比如要计算nums[2]到nums[4]的元素和,根据preSum的公式其实就是用preSum[5] - preSum[2]即可，因为preSum[5]是下标0->4的元素和,preSum[2]是下标0->1的元素和，0->4的元素和减去0->1的元素和就剩下2->4的元素和，即我们要求的。

3.3单调栈

   单调栈的概念非常容易，其实就是栈内的元素严格单调递增或者递减，就是单调栈。这个的作用后面再说我们看看怎么求。 

 

// 单减栈
  let stack = []
  stack.push(0)
  for (let i = 1; i < preSum.length; i++){
      if (preSum[stack[stack.length-1]] > preSum[i]) stack.push(i)
}

  这个一个单调递减栈，从代码中不难看出，如果以栈的栈顶元素为下标，那么其实就是找preSum中比以栈顶元素为下标的preSum元素小的元素的下标入栈。 

3.4本题解题步骤

 

1.    首先将[9,9,6,0,6,6,9]量化，因为本题要求工作大于八小时的天数要严格大于工作小于八个小时的天数，那么大于8小时我们将其变为1，小于8小时变为-1，变为[1,1,-1,-1,-1,-1,1]，那么根据题意其实就是要找一个区间，这个区间的区间和大于0，也就是大于8小时的天数比小于8小时的天数多，就会大于0。而且这个区间得是最长的区间。
2.   区间和可以根据上面介绍的前缀和的办法来求，通过[1,1,-1,-1,-1,-1,1]求前缀和的数组，得前缀和数组为prefixSrc = [0, 1, 2, 1, 0, -1, -2, -1]

          

      到这里我们其实就是要求，使这个sum(i,j)最大的i，j是什么，到这里有两个办法，一个是暴力解法。也就是用双重循环遍历preSum数组，定义一个max变量，遍历过程中不断判断，如果preSum[j]-preSum[i]>0，也就是大于八小时的天数比小于八小时的天数多，就更新为max，遍历结束后，最大的区间和也就求出来了，此题也就解出来了。

  

const longestWPI = (hours) => {
  //求前缀和数组
  let preSum = new Array(hours.length + 1).fill(0);
 
  for (let i = 1; i <= hours.length; i++) {
    //这里这样求是因为如果hours数组中那一天工作时间大于8小时，量化后肯定是正1
    //相反则是负1 所以直接加一减一了 而不是像公式中加nums[i]这样
    if (hours[i - 1] > 8) preSum[i] = preSum[i - 1] + 1;
    else preSum[i] = preSum[i - 1] - 1;
  }
  //求满足条件的最大的区间和
  let max = 0;
  for (let i = 0; i < preSum.length - 1; i++) {
    for (let j = i + 1; j < preSum.length; j++) {
      if (preSum[j] - preSum[i] > 0) {
        max = Math.max(max, j - i);
      }
    }
  }
  return max;
};
console.log(longestWPI([9, 9, 6, 0, 6, 6, 9]));

     另一种办法则是用上面提到的单调栈 ，这里用了单减栈，即栈内元素严格递减的栈， 也就是说这个栈中的元素(也就是下标)对应在preSum数组中都是小于等于0的，也就是首先固定了preSum[j] - preSum[i] >0这个表达式中preSum[i]的部分，因为preSum[i]现在都是小于等于0的,要使preSum[j] - preSum[i]尽量大，那么preSum[i]就要尽量小。

   

const longestWPI = (hours) => {
  //求前缀和数组
  let preSum = new Array(hours.length + 1).fill(0);
 
  for (let i = 1; i <= hours.length; i++) {
    if (hours[i - 1] > 8) preSum[i] = preSum[i - 1] + 1;
    else preSum[i] = preSum[i - 1] - 1;
  }
  // 求单减栈
  let stack = [];
  stack.push(0);
  for (let i = 1; i < preSum.length; i++) {
    if (preSum[stack[stack.length - 1]] > preSum[i]) stack.push(i);
  }
  let max = 0;
  // 这里j从preSum的最后开始是因为 j必须大于stack.pop() 这样才不会一开始就产生负值
  // 因为后面求出的max肯定要比当前的max大才有意义 因为stack.pop()是代表了下标，下标都是大于0的
  // 那么如果后面的结果想要比max大 就需要j至少比当前的max大
  for (let j = preSum.length - 1; j > max; j--) {
    while (stack.length > 0 && preSum[j] - preSum[stack[stack.length - 1]] > 0) {
      max = Math.max(max, j - stack.pop());
    }
  }
  return max;
};
console.log(longestWPI([9, 9, 6, 0, 6, 6, 9]));

 至此，本题结束。