机器学习算法——集成学习4（Bagging）

一、理论

Bagging是并行式集成学习方法最著名的代表，采用自助采样法。

自助采样法是给定包含m个样本的数据集D,对它进行采样产生数据集，每次随机从D中挑选一个样本，将其拷贝放入,然后再将样本放回初始数据集D中，使得该样本在下次采样时仍可能被采到；这个过程重复执行m次后，我们就得到了包含m个样本的数据集,这就是自助采样的结果。这样会造成D中有一部分样本会在中多次出现，而有一部分样本不出现，可以做一个简单的估计，样本在m次采样中始终不被采到的概率是，取极限得到：

即通过自助采样，初始数据集D中约有36.8%的样本未出现在采集数据集中，于是我们可将

用作训练集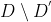，用作测试集。自助采样法在数据集较小、难以有效划分训练/测试集时有用。 但是它改变了初始数据集的分布，会引入估计偏差。在初始数据量足够时，留出法和交叉验证法更常用一些。这样，实际评估的模型与期望评估的模型都使用m个训练样本，而我们仍有数据总量约1/3的、没在训练集中出现的样本用于测试，这样的测试结果称为“包外估计”。

回归正传,Bagging的基本流程是采样出T（T代表训练轮数）个含有m个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再将这些基学习器进行结合。

在对预测输出进行结合时，Bagging通常对分类任务使用简单投票法，对回归任务使用简单平均法。若分类预测时出现两个类收到同样票数的情形，则简单的做法是随机选择一个，可进一步考察学习器的置信度来确定最终胜者。Bagging算法描述为：

---

输入：训练集

          基学习算法

        训练轮数T;

过程：

for t=1,2,...,T do

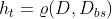          其中是自助采样产生的样本分布

end for

输出: 

---

Bagging能不经修改地用于多分类、回归任务。AdaBoost只适用于二分类任务。

学习方法的泛化能力是由该方法学习到的模型对未知数据的预测能力，是学习方法本质上重要的性质。现实中采用最多的办法是通过测试泛化误差来评价学习方法的泛化能力。泛化误差刻画了学习算法的经验风险与期望风险之间偏差和收敛速度。

Bagging采用的自助采样法有一个优点是约有1/3的样本可用作验证集来对泛化性能进行“包外估计”，为此需要记录每个基学习器所使用的训练样本，不妨设表示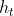实际使用的训练样本集，令表示对样本x的包外预测，即仅考虑那些未使用x训练的基学习器在x上的预测，有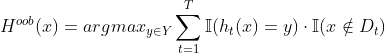

则Bagging泛化误差的包外估计为

 二、在西瓜数据集3.0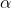上实现Bagging算法

# coding=utf-8
import pandas as pd
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
 
xigua = pd.read_csv('D:/Machine_Learning/西瓜数据集3.0α.csv', encoding='gbk')
data = xigua.values[:, [1,2]]
target = xigua.values[:, 3]
clf = BaggingClassifier(base_estimator=DecisionTreeClassifier(criterion='entropy'),
                        n_estimators=3,  random_state=0).fit(data, target)
print(clf.score(data, target))
print(clf.predict(data))

得到的结果为：